Locação Geométrica
Trataremos neste item da construção de coordenadas, que permitirão mais tarde locar elementos gráficos sobre o desenho.
Tanto a locação geométrica de coordenadas quanto o desenho de elementos básicos (linhas, textos, etc) seguem um esquema semelhante ao usado no TQS-Formas.
Definição de valores numéricos
Valores numéricos são usados em coordenadas, distâncias, ângulos, dimensões, etc. O sistema permite a construção de expressões aritméticas sempre em lugares onde valores numéricos sejam esperados.
Operações básicas
Os seguintes símbolos são usados para expressar as operações aritméticas básicas:
| + | Mais |
| - | Menos |
| * | Vezes |
| / | Dividido |
| ** | Elevado |
| ( ) | Parênteses |
Expressões aritméticas
O sistema interpreta expressões aritméticas de uma forma simplificada: sempre da esquerda para a direita, sem consideração da precedência algébrica dos operadores. Por exemplo:
3 + 4 resulta em 7, enquanto que
3 + 4 * 5 resulta em 35 e não em 23, pois o programa efetua asoma de 3 com 4 primeiro.
Para compensar, o DP permite o uso de parênteses. Na expressão anterior, para multiplicar 4 por 5 primeiro, fazemos:
3 + (4 * 5)
Parênteses podem ser aninhados:
( (3 ** 2) + (4 ** 2) ) ** 0.5 resulta em 5
Funções
Além dos operadores aritméticos básicos, existem funções que podem ser usadas dentro de expressões aritméticas. Uma função é chamada pelo nome, seguida de argumentos entre parênteses:
SEN (x) Seno de um ângulo em graus
COS (x) Coseno
TAN (x) Tangente
ASEN (x) Arco em graus cujo seno vale x
ACOS (x) Arcoseno
ATAN (x) Arcotangente
RAIZ (x) Raiz quadrada de um número
FIX (x) Parte inteira de um número
FRAC (x) Parte fracionária de um número
ABS (x) Valor positivo de um número
A função SEN pode ser chamada também de SIN, e a função RAIZ de SQRT. Exemplo de expressão aritmética com tangente:
(90 + 12) / TAN (60)
Operadores Geométricos
Além das funções mostradas acima, existem operadores geométricos, que serão mostrados em detalhe adiante. Estes operadores trabalham sobre nós, e retornam um valor que pode ser usado normalmente dentro de uma expressão aritmética:
DIS nno1 nno2 Distância entre 2 nós
DX nno1 nno2 Delta X entre 2 nós
DY nno1 nno2 Delta Y entre 2 nós
X nno X de um nó
Y nno Y de um nó
DIR nno1 nno2 Direção de 2 nós
Por exemplo, DIS 5 6 representa a distância entre os nós 5 e 6 e X10 a abscissa do nó 10. O conceito de nós será visto logo adiante.
Ângulos
Ângulos são valores numéricos, que podem ser formados por qualquer tipo de expressão aritmética. Todos os ângulos definidos na entrada de dados são em graus decimais.
Ângulos podem ser definidos também em graus, minutos e segundos. A sintaxe é:
graus ^ minutos segundos
O caractere (^) avisa ao sistema que a seguir seguem medidas angulares em minutos e segundos. Por exemplo,
30 ^ 10 20
significa 30, 10 minutos e 20 segundos. O mesmo valor decimal vale 30.1722.
Expressões lógicas e outras funções
Expressões lógicas, usadas em comandos condicionais podem fazer parte de expressões numéricas. O seu uso será visto no capítulo Controle de fluxo.
Funções de manipulação de valores alfanuméricos (cadeias de caracteres) também podem fazer parte de expressões numéricas, e seu uso será visto no capítulo Variáveis e macro-substituição.
Nós e coordenadas
Todos os elementos gráficos são armazenados em função de suas coordenadas XY. Nós são coordenadas que recebem um número de identificação (número entre 1 e 30.000). A vantagem de se construir nós é que uma vez definidas suas coordenadas, estas podem ser reutilizadas qualquer número de vezes, apenas referenciando-se o número do nó. Outras aplicações, tais como o TQS-Formas usam nós também como base para definição de todos os outros elementos.
Nós são definidos através de um par de coordenadas, mas um par de coordenadas também pode ser definido em função de outros nós existentes. Vamos então mostrar a construção de coordenadas e de nós gradativamente.
Nós e outros elementos de desenho são construídos dentro da seção de DESENHO. Para testar os exemplos a seguir, é necessário abrir primeiro esta seção.
Modos de definição de nós
Nós podem ser definidos de 4 modos:
nno coord
OFFSET valor coord1 coord2
INTERSECCAO linha linha
PROJECAO coord1 coord2 coord3
onde:
nnon úmero de um nó
valor valor numérico
coordum par de coordenadas
linha duas coordenadas ou um par de coordenadas e um ângulo
No primeiro caso, define-se o nó por suas coordenadas. Por exemplo:
15 300, 10
significa: Nó 15, nas coordenadas (300, 10). A definição completa do que podem ser coordenadas será vista logo a seguir.
Nos casos de OFFSET, INTERSECÇÃO e PROJEÇÃO são feitas construções geométricas que resultam nas coordenadas de um nó; nos 3 casos, usa-se a definição de coordenadas.
Definição de coordenadas
Coordenadas podem ser absolutas ou relativas a nós existentes, e os valores X, Y (ou distância e ângulo) podem ser compostos por expressões aritméticas.
Coordenadas absolutas
A forma mais simples de definição de um par de coordenadas é pelo seu valor:
x,y
Assim, em:
15 300,10
definimos as coordenadas (300,10) como sendo do nó 15. Uma segunda alternativa para a definição do valor das coordenadas é pelo formato polar:
distância < ângulo
Por exemplo, em:
20100 < 45
temos o nó 20 à distância da origem (0,0), formando um ângulo de 45 em relação ao eixo X (coordenadas (70.7, 70.7)).
Coordenadas relativas
Pode-se definir um par de coordenadas a partir de outro par, de um nó existente. As variações possíveis são:
nno
nno @ dx, dy
nno @ dist < ângulo
No primeiro caso, as coordenadas resultantes são as coordenada do nó de número nno. Isto significa que sempre no lugar de um par de coordenadas podemos fornecer o número de um nó.
No segundo caso, são as coordenadas do nó fornecido mais um deslocamento (dx,dy).
No terceiro caso, são as coordenadas do nó fornecido, mais uma distância e um certo ângulo em relação ao eixo X. Por exemplo:
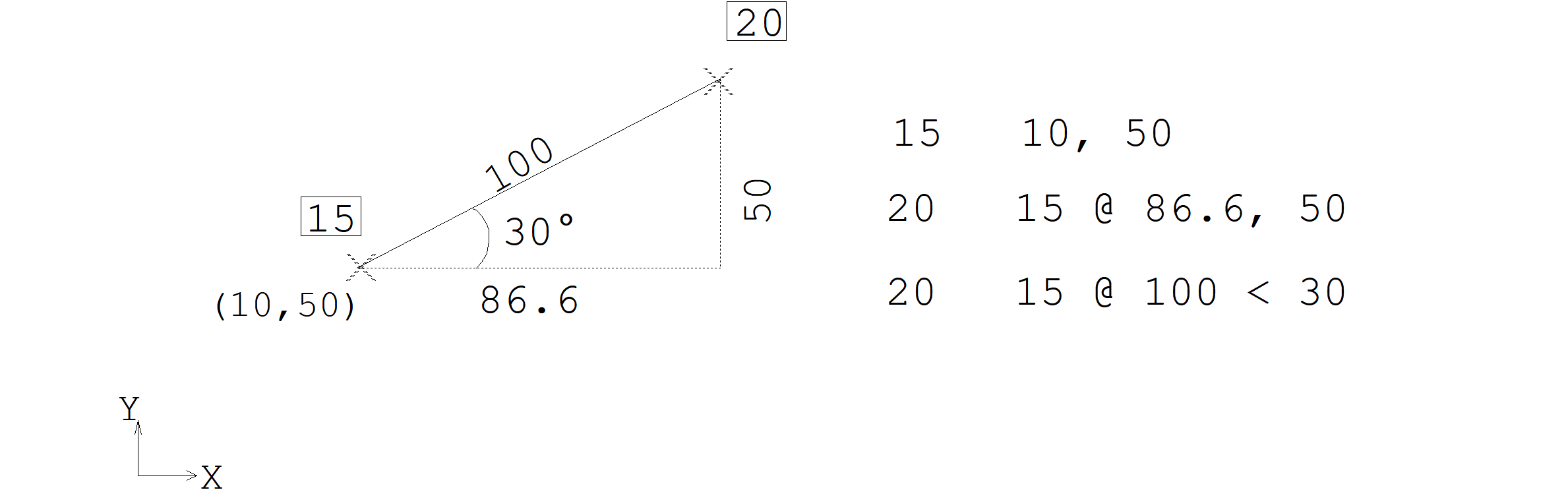
Na figura temos:
- O nó 15 nas coordenadas (10,50).
- O nó 20, nas coordenadas do nó 15, mais 86.6 de deslocamento na direção X e 50 de deslocamento na direção Y.
- O mesmo nó 20, definido de forma diferente: está à distância 100 do nó 15, formando a direção 15-20 um ângulo de 30 em relação ao eixo X.
Uso de expressões aritméticas
Quando codificamos coordenadas X,Y fornecemos 2 valores: um para X e um para Y. No lugar de valores numéricos, o sistema permite o fornecimento de expressões aritméticas, com funções e operadores geométricos vistos anteriormente.
A principal vantagem da interpretação de expressões aritméticas é que em vez do projetista calcular as coordenadas exatas de cada nó fazendo as contas manualmente, ele pode especificar diretamente quais foram às operações que o levaram a um determinado par de coordenadas. Com isto, ficam autodocumentadas as construções geométricas e aritméticas que levaram a locação de cada nó; mais tarde, se houver um erro qualquer na definição do desenho, será muito mais fácil a verificação da posição de cada nó.
No exemplo a seguir, vemos dois modos de construção do nó partir do nó 17, compondo medidas com expressões aritméticas. O segundo modo será explicado logo a seguir.
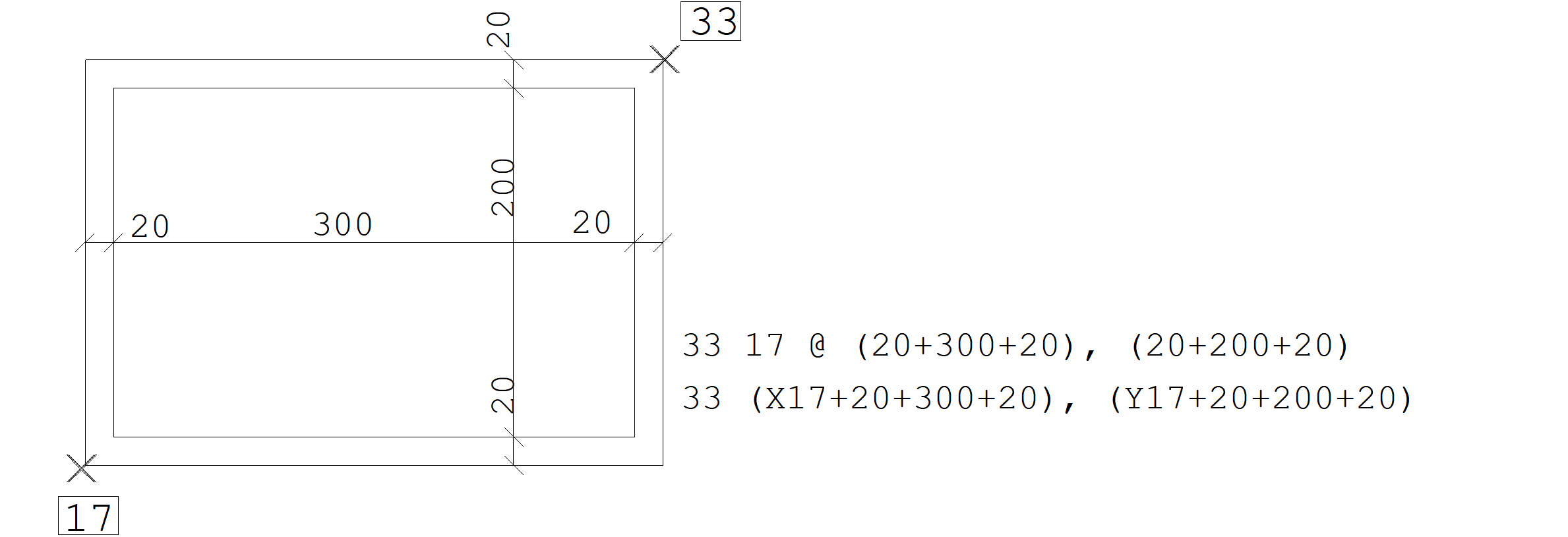
Abscissas e ordenadas de nós conhecidos
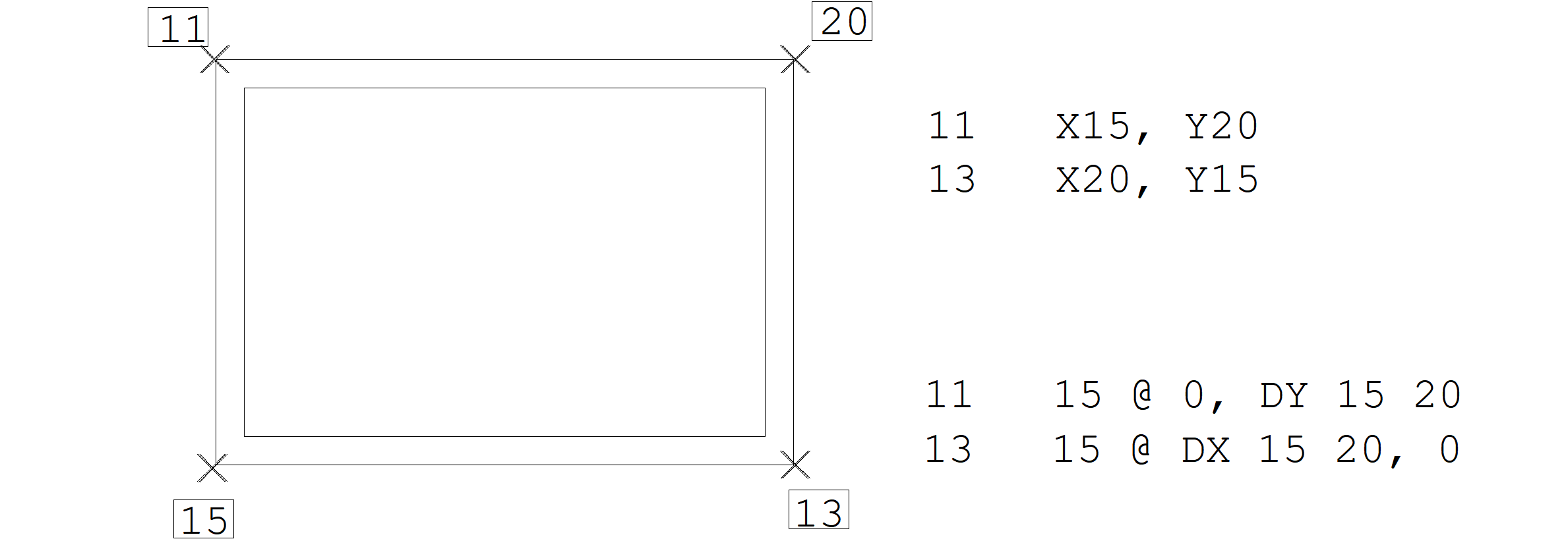
Quando usamos o caractere @ para a entrada de valores relativos a um nó, estamos tomando como valor inicial o X e o Y do mesmo nó. Existe um modo de tomarmos ordenadas e abscissas de nós diferentes para a definição de um outro nó. Para isto são usados os operadores:
X nno
Y nno
Onde nno é o número do nó do qual estamos tomando a abscissas X ou ordenada Y. É importante lembrar que para o programa, X nno e Y nno se comportam como valores simples, e como tais podem ser combinados a outros por meio de operações aritméticas. No exemplo a seguir, definimos os nós 11 e 13 do canto de um retângulo em função do X e Y dos nós 15 e 20 já definidos (os exemplos com DX e DY serão explicados a seguir).
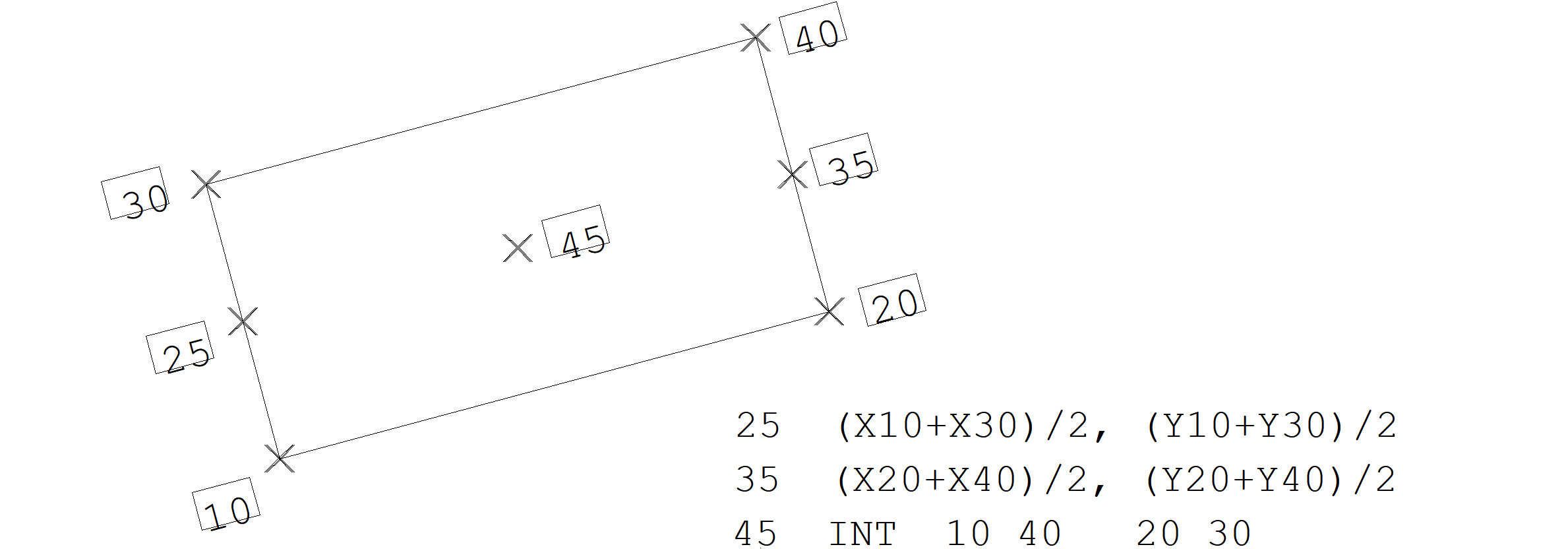
No próximo exemplo, os nós 25 e 35 são colocados no ponto médio entre os nós 10 e 30, e 20 e 40.
Deslocamentos e distâncias entre nós
Outra opção para a entrada de valores são os operadores
DX nno1 nno2
DY nno1 nno2
DISTANCIA nno1 nno2
No primeiro caso, o valor resultante é a diferença entre o X do nó nno2 e o X do nó nno1. O segundo caso é semelhante, mas os valores tomados são de Y. A entrada de DX e DY geralmente é feita em definições relativas a nós, no formato deltax, deltay.
No terceiro caso, a resultante é a distância entre os nós nno1 e nno2. Este tipo de definição é geralmente utilizada em definições relativas a nós, no formato distância < ângulo.
Ângulos entre nós
Muitas vezes, a direção formada por 2 nós é paralela a direção de outros 2 nós já definidos. Em outros casos, a direção formada por 2 nós forma um ângulo conhecido em relação a outra direção conhecida que não o eixo X. Para isto, existe um modo de definição de ângulos, que retorna uma direção conhecida. Esta direção então pode ser alterada para formar a direção desejada.
DIRECAO nno1 nno2
Onde nno1 e nno2 são números de nós já definidos. Não devemos esquecer que ângulos são positivos sempre no sentido anti-horário. Na figura a seguir, o nó 32 (a ser definido) forma com o nó 21 um ângulo de 30 no sentido horário (negativo) em relação à direção dos nós 13 e 21.
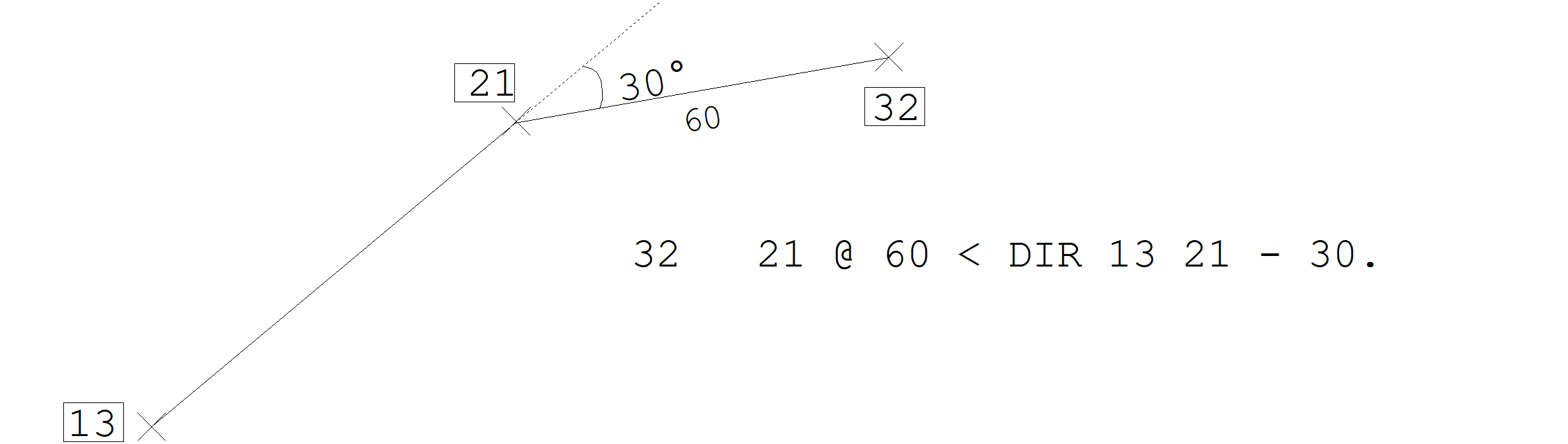
Uso de funções trigonométricas
O modo polar de entrada de coordenadas (distância < ângulo) resolve os casos onde são conhecidos um ângulo e uma hipotenusa de um triângulo retângulo. Para resolvermos problemas onde são conhecidos apenas um ângulo e um cateto, é necessário o uso de funções trigonométricas, tal como no exemplo seguinte. Vamos determinar as coordenadas do nó partir do nó 10:
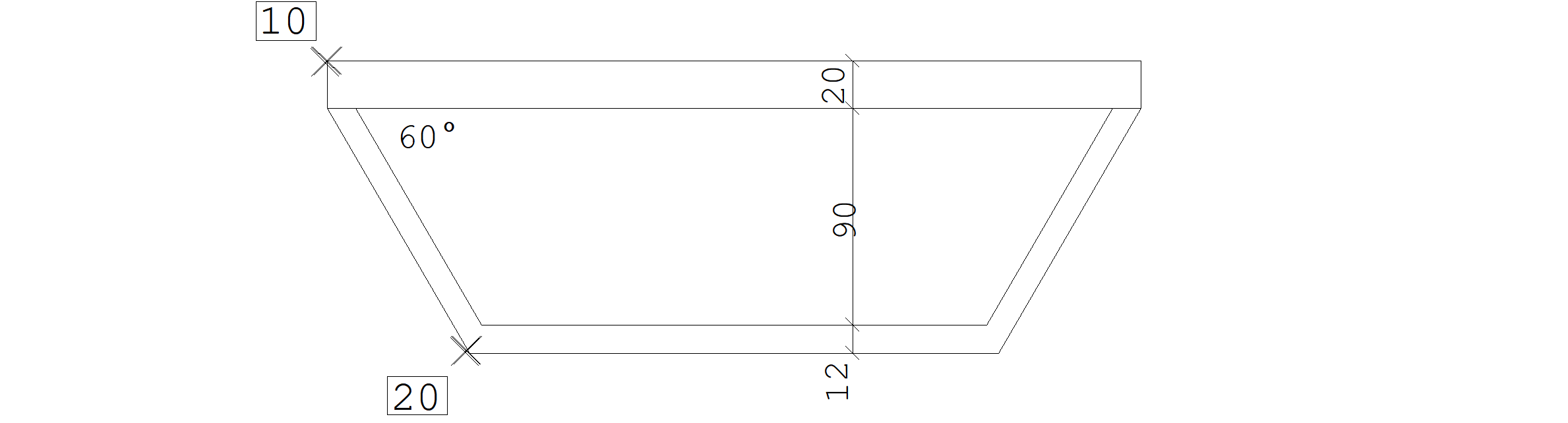
20 10 @ (90 + 12)/TAN (60), -(20 + 90 + 12)
Uso de coordenadas
Comandos de desenho tais como POLIGONAL para traçado de linhas conectadas tem uma sintaxe que exige a entrada de coordenadas. Por exemplo:
POLIGONAL coord1; coord2; ....
Resumindo o que vimos, um par de coordenadas pode ser:
x , y
dist < ang
nno
nno @ dx , dy
nno @ dist < ang
onde cada um dos valores numéricos pode ser dado por uma expressão aritmética.
OFFSET
Um nó pode ser definido por um offset em relação a uma reta:
nno OFFSET valor coord1 coord2
O comando OFFSET permite uma forma simplificada de se definir nós que formam um ângulo de 90 com uma determinada direção. O nó resultante está a uma distância fornecida dos pontos 1-2, na altura do ponto 2, e a direita da direção 1-2 se a distância for positiva.
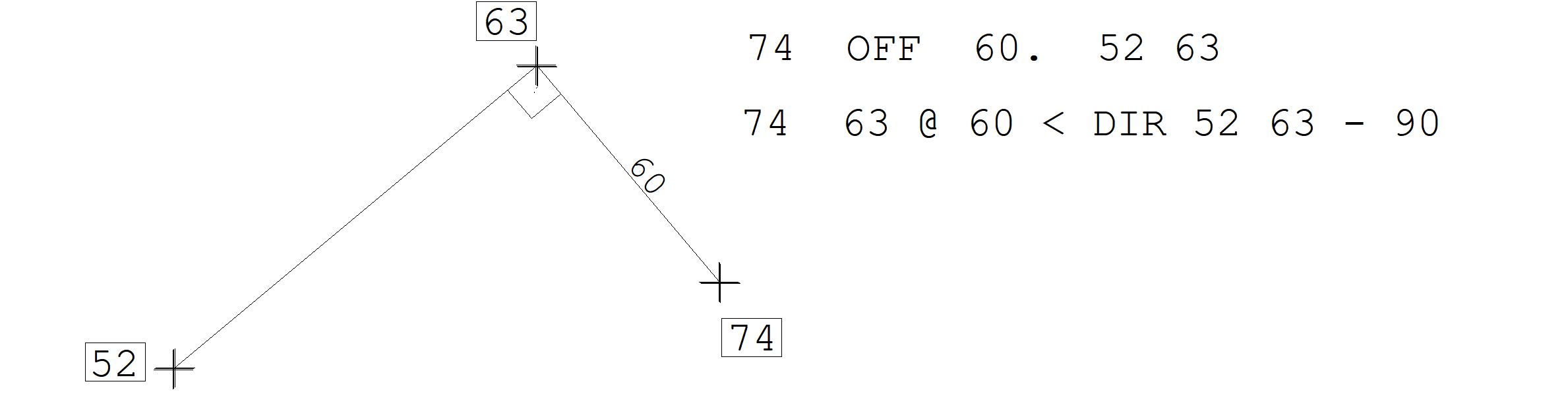
Note que o comando OFFSET pode ser substituído (com um pouco mais de trabalho) por uma definição de coordenada relativa.
INTERSECÇÃO
O comando INTERSECÇÃO determina as coordenadas de um nó resultante da intersecção de duas linhas:
nno INTERSECCAO linha1 linha2
Cada uma das linhas pode ser definida por duas coordenadas ou pelo par: coordenadas e um ângulo:
coord1 coord2
coord ANG angulo
Numa das figuras anteriores nós vimos uma intersecção realizada pelo fornecimento de 4 pontos, cada 2 definindo uma linha. Na figura abaixo uma intersecção entre faces de pilares é feita com duas linhas definidas por ponto e ângulo:

PROJEÇÃO
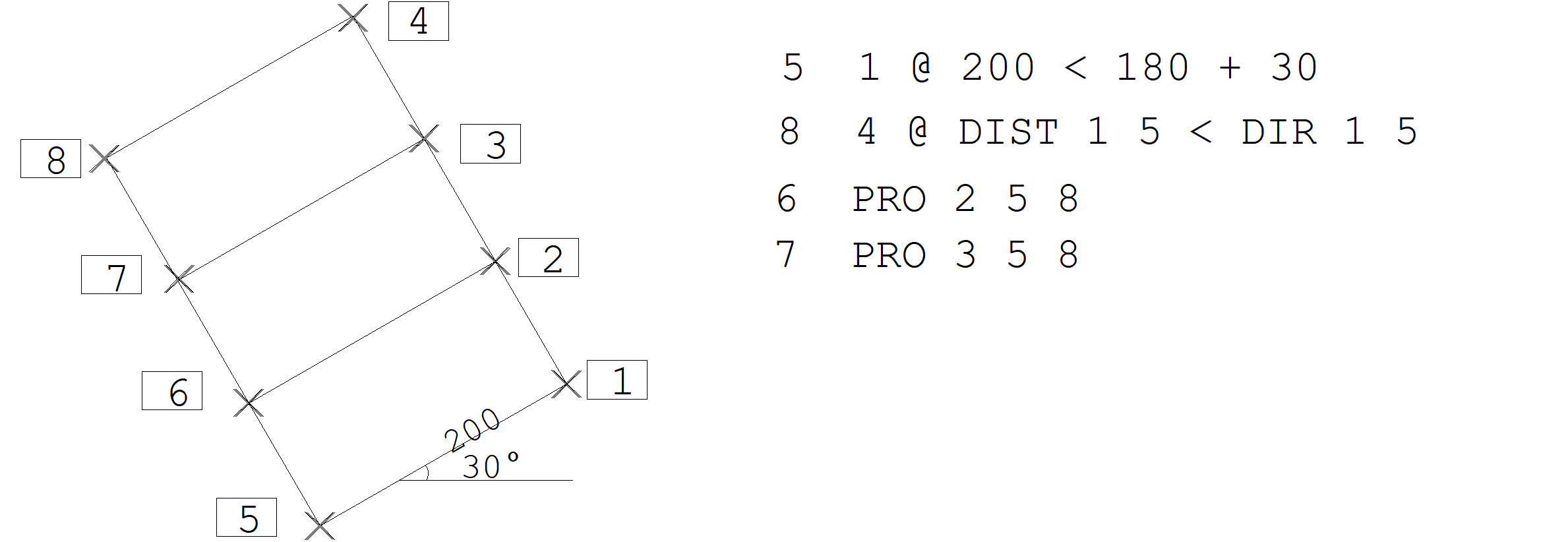
O comando PROJEÇÃO projeta ortogonalmente as coordenadas coord1 sobre uma reta formada pelas coordenadas coord2 e coord3:
nno PROJECAO coord1 coord2 coord3
No exemplo a seguir, os nós 1, 2, 3 e 4 já estão definidos; os nós 6 e 7 são obtidos por meio de projeção.
Sistema local de coordenadas
É muito comum encontrarmos desenhos onde grandes quantidades de linhas sejam paralelas a direções diferentes dos eixos X e Y do sistema global de coordenadas. A definição destas linhas seria muito trabalhosa pela entrada de distâncias e ângulos.
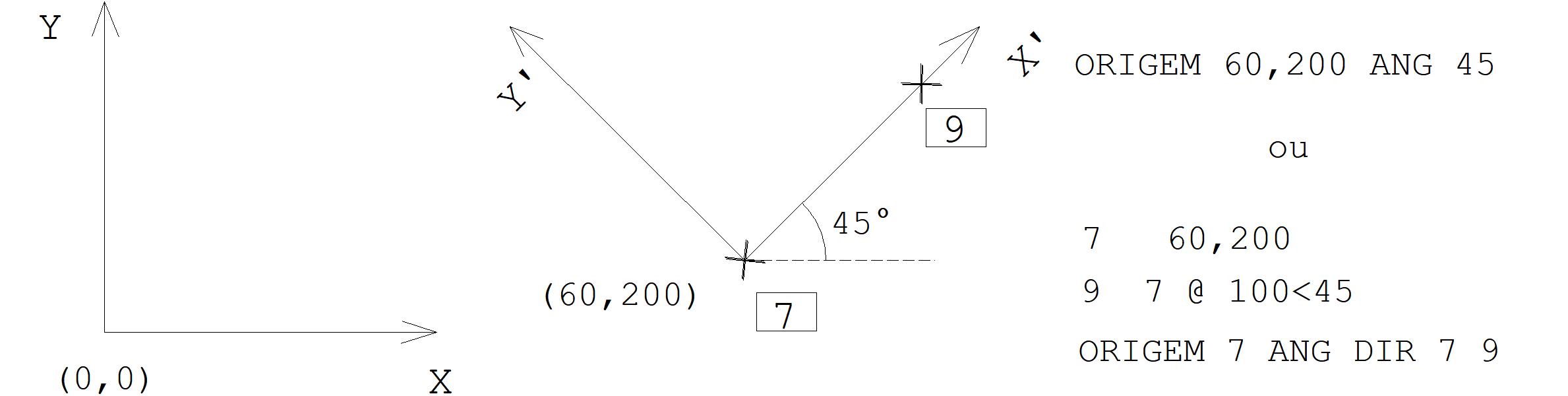
Para cobrir estes casos, o sistema permite definir a qualquer momento um sistema local de coordenadas, transladado e girado em relação ao sistema global. No início do processamento, o chamado Sistema Local Atual coincide com o sistema global, com origem (0,0) e ângulo de rotação de zero grau.
Todas as entradas de ângulos, distâncias e deltas são sempre medidas em relação ao sistema local atual de coordenadas. O comando LISTAR (pág. 102) também mostra a coordenadas de nós pelo sistema local atual.
A sintaxe é:
ORIGEM [coord] [ANGULO angulo]
coord são as coordenadas do sistema local medidas em relação ao sistema global de coordenadas. Se estas coordenadas não forem fornecidas serão assumidas (0,0).
ângulo é o ângulo de rotação do sistema em relação ao eixo X do sistema global. Se o ângulo não for fornecido, será adotado zero (e, portanto somente a palavra ORIGEM é suficiente para retornar o sistema de coordenadas para o global).
Todas as coordenadas são armazenadas internamente pelo sistema global de coordenadas. A plotagem do desenho é feita sempre com o eixo X global paralelo ao papel, e é independente da posição do desenho em relação aos eixos globais.
Geração de nós
Para a definição de nós em desenhos de geometria uniforme, existem comandos de geração em linha e em malha.
Geração de nós em linha
Nós podem ser gerados ao longo de uma linha, com espaçamento e numeração uniforme. A sintaxe para definição desta geração consiste numa extensão do comando de definição de nós. Após a definição do nó (por coordenadas ou construção geométrica) define-se opcionalmente os dados de geração, conforme mostra a figura seguinte:

10 10,50 A 35 PASSO 5 15,5
Aqui vemos o nó 10 definido nas coordenadas (10,50). Foram gerados a partir do nó 10, os nós 35, com numeração aumentando de 5 em 5 e incremento de coordenadas delta-x de e delta-y de . A sintaxe completa do comando é:
nno coord[A nno2 [PASSO num ] coord2 ]
Este comando define os nós nno até nno2, com incremento de numeração num e incremento de coordenadas coord2 a partir de coord. O passo de incremento de número de nó é opcional, e quando não fornecido é assumido 1.
A geração de nós em linha na verdade pode ser feita a partir de qualquer definição de nó, incluindo os comandos de construção geométrica, como por exemplo:
50 PRO 40 21 22 A 60 10,10
Neste comando, o nó 50 foi criado a partir da projeção do nó 40 sobre a reta 21-22. Os nós 60 foram criados então, com incrementos de coordenadas de (10,10), a partir do nó 50.
Geração de nós em malha
Na geração de nós em malha, pode-se gerar um conjunto de nós de numeração uniforme, mas de espaçamento irregular. A geração consiste em interceptar dois conjuntos de retas em duas direções diferentes, cada reta definida por um nó e uma direção.
Para poder fazer uso da geração em malha, é necessário antes planejar uma numeração uniforme dos nós da malha. A figura seguinte mostra um exemplo típico de geração de uma malha de nós:

Nesta figura foram interceptados dois conjuntos de retas: o conjunto dos nós 14 (passo 1 default), com ângulo de 90 (default) e o conjunto dos nós 50 (passo 10) com ângulo de zero graus (default). Os nós resultantes das intersecções foram numerados a partir do segundo conjunto, com o incremento de numeração do primeiro conjunto. Note que:
- Os nós 11, 12, 13 e 14 foram previamente criados, e não tem espaçamento necessariamente regular.
- Os nós 20, 30, 40 e 50 foram previamente criados, e também não tem espaçamento necessariamente regular.
- As retas passando pelos nós 14 tem um ângulo de 90.
- As retas passando pelos nós 50 tem um ângulo de zero grau.
- A numeração de cada nó gerado é feita por linha, usando-se o número do nó a esquerda, incrementado pelo passo de numeração do conjunto 1 de nós.
- A numeração dos nós 14 e 50 foi planejada para ser regular, e não criar "choques" de numeração dos nós gerados.
A sintaxe completa do comando de geração é:
MALHA conjunto-1 conjunto-2
onde conjunto refere-se a um conjunto de linhas formadas por um nó e uma direção. Cada conjunto é codificado da seguinte forma:
nno1 A nno2 [PASSO num] [ANG angulo]
O passo de numeração de nós é opcional, e se não fornecido é adotado 1. O ângulo opcional define a direção de intersecção das retas do conjunto. O default deste ângulo é de 90 para o conjunto 1 e de zero graus para o conjunto 2.
