Aspectos Teóricos
Concreto Protendido
O concreto protendido surgiu para atender a necessidade de se diminuir as tensões de tração no concreto. Através da protensão são introduzidos esforços externos que equilibram as ações externas, limitando as tensões normais de tração. Consequentemente, o problema da fissuração, existente no concreto armado, é minimizado e a deformabilidade da estrutura é diminuída sensivelmente.
Definição
A norma NBR-6118:2003 define concreto protendido como: "Aqueles nos quais parte das armaduras é previamente alongada por equipamentos especiais de protensão com a finalidade de, em condições de serviço, impedir ou limitar a fissuração e os deslocamentos da estrutura e propiciar o melhor aproveitamento de aços de alta resistência no estado limite último (ELU)." Por essa definição nota-se que o dimensionamento das peças protendidas é feito, em primeira instância, para os estados limites de serviço (ELS).
Ideias básicas
A ideia fundamental da protensão é comprimir as regiões da estrutura que serão tracionadas pela ação do carregamento externo. Portanto, o ideal é que os diagramas de esforços decorrentes da protensão sejam equilibrantes e contrários aos das ações externas.
O projeto de lajes de concreto protendido é muito similar ao projeto de lajes de concreto armado. Os cabos de protensão funcionam, resumidamente, como ações externas aplicadas a laje. Estas forças têm duas componentes básicas:
- Ação de uma força de compressão centrada;
- Forças de alívio aplicadas ao concreto devido a ação de retificação do cabo quando este é tracionado.
Devido à ação destas forças externas provenientes dos cabos, novos carregamentos devem ser introduzidos no modelo estrutural da laje (grelha ou pórtico) para a sua correta consideração.
A participação dos cabos no comportamento a flexão da laje depende basicamente do tipo de protensão. Quando o cabo é aderente, ele também participa diretamente da seção, pois não há deslizamento entre o concreto e o cabo em cada seção, o que não ocorre com o cabo engraxado, que também ajuda na resistência da seção mas com uma participação diferente pois a seção transversal do cabo deforma diferentemente da seção do concreto.
Outro aspecto importante no projeto das lajes de concreto protendido em comparação ao concreto armado é que as verificações em serviço devem ser feitas para diversos estágios de carregamento da estrutura. No concreto armado, no caso mais geral, estamos acostumados a verificar os elementos estruturais apenas para o estágio final do carregamento.
No concreto protendido, devido à introdução do carregamento adicional provocado pelos cabos numa época em que o concreto ainda é jovem, devem-se fazer verificações adicionais para diversos estágios da construção. Assim, diferentemente do CA (concreto armado), damos ênfase especial neste sistema de lajes protendidas a definição mais precisa de estágios de carregamentos na estrutura e que tipo de verificação deve ser realizada em cada caso. Aparecerão estágios como: Ato da Protensão, Combinações Quase-Permanentes, Combinações Frequentes, Estado Limite Último, etc.
Para um entendimento melhor de como estas combinações são definidas e quais verificações devem ser realizadas, reproduzimos a seguir, de forma simplificada os conceitos contidos na norma de concreto NBR6118:2003.
Vantagens da protensão
Em relação ao concreto armado convencional podem ser relacionadas as seguintes vantagens [referência bibliográfica 1]:
- Maior durabilidade da estrutura pela ausência ou redução drástica da fissuração;
- Estruturas com maiores vãos livres;
- Construções mais rápidas;
- Redução da quantidade de materiais: concreto e aço, em função da utilização de maiores resistências;
- Menor deformabilidade do que as estruturas de concreto armado, considerando-se para um mesmo vão e estruturas adequadamente dimensionadas;
- Facilidade de recuperação após um super-carregamento. Eventuais fissuras se fecham após o descarregamento;
- Maior resistência à fadiga: as variações de tensões no aço são pequenas pelo fato da protensão fazer com que toda a seção de concreto trabalhe;
- Reduz as tensões principais de tração provocadas pelas solicitações tangenciais;
- A aplicação da protensão constitui uma prova de carga para estrutura. Em geral tanto o aço como o concreto ficam submetidos na operação de protensão a tensões maiores do que as que poderão ocorrer durante a vida da estrutura.
Cuidados com a protensão
Como a integridade dos elementos estruturais depende, basicamente, de alguns cabos submetidos a uma tensão elevada e suas ancoragens, alguns cuidados devem ser tomados na execução de estruturas protendidas. Entre eles podemos citar [referência bibliográfica 1]:
- Maior controle tecnológico dos materiais;
- Atenção ao problema da corrosão, que é muito danoso em aços tensionados;
- Durante a execução da estrutura, precisão no posicionamento das armaduras protendidas;
- As operações de protensão exigem equipamentos e pessoal especializado.
Normas
A seguir são relacionadas às normas da ABNT mais importantes para o projeto e execução do concreto protendido:
- NBR 6118: Projeto de Estruturas de Concreto;
- NBR 6120: Cargas para o Cálculo Estruturas de Edificações
- NBR 7480: Aços Destinados a Armaduras de Concreto Armado;
- NBR 7482: Fios de Aços para Concreto Protendido;
- NBR 7483: Cordoalhas de Aço para Concreto Protendido;
- NBR 8681: Ações e Segurança nas Estruturas.
Estados Limites de Serviço
O dimensionamento das lajes de concreto protendido, de acordo com as recomendações das normas NBR 6118 (item 19.3) e NBR 8681, impõe a verificação à segurança das estruturas em relação aos seguintes Estados Limites de Serviço:
- Estado limite de deformação (sub-item 17.3.2 da NBR 6118): estado no qual um ou mais pontos do plano da laje alcança os máximos valores estabelecidos para a utilização normal da estrutura para a combinação de ações quase-permanente.
- Estado limite de descompressão (sub-item 17.3.3 da NBR 6118): estado no qual em um ou mais pontos da seção transversal da laje a tensão normal é nula, não havendo tração no restante da seção para as combinação de ações quase-frequentes.
- Estado limite de formação de fissuras (sub-item 17.3.4 da NBR-6118): estado em que se inicia a formação de fissuras. Admite-se que este estado limite seja atingido quando a tensão de tração máxima na seção seja igual a fct,f
- Estado limite de abertura de fissuras (sub-item 17.3.3 da NBR-6118): estado em que as fissuras se apresentam com aberturas características de valores especificados (wk ≤ ) para as combinação de ações frequentes.
Estados Limites Últimos relativos à flexão
No dimensionamento à flexão de estruturas de concreto protendido a sua segurança deve ser verificada com relação ao aparecimento dos estados limites últimos devidos a:
- Ato da Protensão: as tensões normais não devem ultrapassar determinados valores para os carregamentos especificados para o Ato da Protensão. Coeficientes ponderadores específicos são definidos neste caso.
- Tempo Infinito: as solicitações normais oriundas do carregamento último das ações, ponderadas pelos respectivos coeficientes de majoração, não devem provocar deformações excessivas na seção transversal (encurtamento do concreto e/ ou alongamento da armadura).
Referências Bibliográficas
[1] Apostila de Concreto Protendido da Escola de Engenharia Mackenzie, Luiz Cholfe, 1991;
[2] Lajes em Concreto Armado e Protendido, Vicente C. Moreira de Souza e Albino J.Pimenta da Cunha, Editora da Universidade Federal Fluminense, 1994;
[3] Concreto Protendido, Walter Pfeil, Livros Técnicos e Científicos Editora Ltda,1988;
[4] Manual Prático para a Correta Utilização dos Aços no Concreto Protendido,
A. C. Vasconcelos, L.T.C.;
[5] Notas de Aula do Curso Introdução e Prática de Projetos de Lajes Protendidas, Evandro Porto Duarte, 1995;
[6] Projeto e Cálculo de Lajes Protendidas –1995 – Engo Evandro Porto Duarte;
[7] Concrete Society – Technical Report no.43 Pos-tensioned Concrete Floors – Design Handbook;
[8] Terceira Jornada Íbero – Latina – Americana de Concreto Protendido –1994 – Concreto Protendido em Edifícios – Prof. Dr. Mário Franco.
Classificação das Ações e suas Combinações
Segue abaixo uma explicação de todas as "Ações" e suas "Combinações".
Classificação das ações
A NBR-8681: Ações e Segurança nas Estruturas classifica as ações segundo a sua variabilidade no tempo da seguinte forma:
- Ações permanentes: aquelas que ocorrem com valor constante ou com pequena variação durante praticamente toda a vida da construção (50 anos).
- Diretas: peso próprio, elementos permanentes, equipamentos fixos, empuxos etc.;
- Indiretas: protensão, deformações impostas, retrações etc.
- Ações variáveis: apresentam valores com variações significativas em torno de sua média, durante a vida da construção: vento, cargas acidentais, pressões hidrostáticas, temperatura, frenagem etc.
- Normais: probabilidade de ocorrência grande com consideração obrigatória no projeto;
- Especiais: cargas acidentais especiais, por exemplo, ações sísmicas;
- Ações excepcionais: probabilidade de ocorrência muito baixa e com duração extremamente curta (horas): choques, explosão, incêndios.
Combinações de Utilização das ações
Ainda segundo a NBR 8681: "Os estados limites de serviço decorrem de ações cujas combinações podem ter três diferentes ordens de grandeza de permanência na estrutura". Nessas combinações comparecem sempre todas as ações permanentes, incluindo deformações impostas e as ações variáveis correspondentes a cada um dos seus tipos, conforme indicado a seguir:
- Combinações quase-permanentes de utilização são aquelas que podem atuar durante grande parte do período de vida da estrutura, da ordem de metade desse período. Nessas combinações todas as ações variáveis são consideradas com os seus valores quase-permanentes :
- Combinações frequentes de utilização são aquelas que se repetem muitas vezes durante o período de vida da estrutura, da ordem de 105 vezes em 50 anos, ou que tenham duração total igual a uma parte não desprezível desse período, da ordem de 5% (2,5 anos). Nessas combinações a ação variável principal FQ1 é tomada com seu valor frequente e todas as demais ações variáveis são tomadas com seus valores quase-permanentes :
Combinação Última das ações
As combinações últimas de ações são expressas como:
Obs: Os valores de 0 , 1 e 2 correspondentes aos diversos tipos de ações podem ser encontrados na NBR 8681 e na NBR 6118.
Tipos de Protensão
Segundo a NBR protensão, relativa aos estados limites de serviço e relacionadas a exigências de durabilidade, pode ser completa, limitada ou parcial, de acordo com as seguintes definições que serão mostradas nos próximos itens.
Protensão completa – Nível 3
Existe protensão completa quando se verificam as duas seguintes condições:
- Para as combinações frequentes de ações, previstas no projeto, é respeitado o estado limite de descompressão;
- Para as combinações raras de ações, quando prevista no projeto, é respeitado o estado limite de formação de fissuras1.
Protensão limitada – Nível 2
Existe protensão limitada quando se verificam as duas seguintes condições:
- Para as combinações quase-permanentes de ações, previstas no projeto, é respeitado o estado limite de descompressão1;
- Para as combinações frequentes de ações, prevista no projeto, é respeitado o estado limite de formação de fissuras1.
Protensão parcial – Nível 1
Existe protensão parcial quando se verifica a seguinte condição:
- Para as combinações frequentes de ações, prevista no projeto, é respeitado o estado limite de abertura de fissuras, com wk .
A NBR 6118 (na tabela 13.3) estabelece que para meio ambiente não agressivo, como no interior de edifícios em que uma alta umidade relativa somente pode ocorrer durante poucos dias por ano (o que equivale a CAA I e CAA II, conforme item 6.4.2 da norma), pode-se adotar a Protensão Parcial – Nível 1.
Detalhes Normativos de Projeto
A seguir são descritas umas série de orientações para o "Lajes Protendidas". Essas orientações foram extraídas do item 13.2.4 da NBR 6118 (válidas para lajes lisas e cogumelos) e da referência bibliográfica [2] (válidas para lajes cogumelo). Entenda-se por laje cogumelo uma laje apoiada em pilares com capitéis, entenda-se por laje lisa uma laje apoiada em pilares sem capitéis.
Outra referência muito importante é a referência bibliográfica [7] que trata com bastante detalhes e para vários tipos de lajes, quais as espessuras recomendadas.
Esbeltez das lajes protendidas
Neste texto, a esbeltez da laje é definida como a relação entre o menor vão da laje l e a sua espessura h.
Para a escolha da espessura de lajes cogumelos protendidas o ACI-ASCE recomenda a adoção de valores tomados a partir da tabela abaixo:
| Valores Máximos para a Esbeltez (l / h) | |
| Lajes com sobrecarga de 3 kN/m2 | 45 |
| Lajes de cobertura | 48 |
Já a NBR 6118 (itens 13.2.4.1.e e 13.2.4.1.f) estabelece para lajes com protensão o seguinte:
- Valores mínimos para a espessura da laje:
| Valores Mínimos de Espessura (h) | |
| Lajes apoiadas em vigas | |
| Lajes lisas (com ou sem protensão) | |
| Lajes cogumelo (com ou sem protensão) |
- Valores máximos para esbeltez:
| Valores Máximos para a Esbeltez (l / h) | |
| Lajes de piso bi-apoiadas | 42 |
| Lajes de piso contínuas | 50 |
Modulação dos vãos
A referência bibliográfica [2] cita como modulação ideal do ponto de vista econômico para lajes cogumelo a seguinte:
- vãos intermediários iguais entre si;
- vãos extremos com comprimentos da ordem de 80% a 85% dos vãos internos;
- balanços da ordem de 25% a 35% do vão adjacente, dependendo se há ou não parede carregando sua extremidade.
Distribuição dos cabos em planta
Os esforços nas lajes tendem a concentrar-se nas faixas dos pilares. Desta forma o ACI-ASCE recomenda que se concentre cabos ao longo de "faixas de apoio" unindo os pilares, ao invés de uma distribuição uniforme. A seguir são apresentados motivos que justificam tal distribuição para os cabos [referência bibliográfica 2]:
- melhor aproximação dos esforços decorrentes da protensão com os da distribuição de momentos da laje;
- aumento da resistência à punção;
- aumento da resistência próximo ao pilar para transferência de momento na ligação laje-pilar.
Espaçamento mínimo e máximo entre cabos
A distribuição dos cabos em planta deve respeitar espaçamentos mínimos e máximos entre os mesmos.
O espaçamento mínimo depende do tipo de ancoragem utilizada, portanto varia de fabricante para fabricante.
A NBR 6118 (item 18.6.2.3) exige os seguintes espaçamentos mínimos, medidos entre faces das bainhas, para as armaduras de protensão, no caso de bainhas isoladas:
- espaçamento horizontal mínimo: MAX(ext , 4cm);
- espaçamento vertical mínimo: MAX (ext , 5cm)
onde: ext - diâmetro externo das bainhas.
O espaçamento máximo tem como objetivo garantir que os esforços atuantes na laje sejam bem distribuídos em toda a sua extensão. Segundo [referência bibliográfica 2] o espaçamento máximo (horizontal) não deve ultrapassar:
- s 6h nas faixas centrais
- s 4h nas faixas dos pilares
Os valores para os espaçamentos devem ser fornecidos no arquivo de critérios do sistema.
Cobrimento das armaduras de protensão
A NBR 6118 (item 7.4) estabelece os seguintes valores para cobrimento cnom das armaduras de protensão nas lajes:
- função do meio ambiente (com Δc = ):
- CAA I: cnom ;
- CAA II: cnom ;
- CAA III: cnom ;
- CAA IV: cnom ;
- função do diâmetro da bainha (ext ):
- cnom 0,5 ext.
- função do diâmetro do agregado ( agreg ):
- cnom 0,83 agreg.
Os valores para o cobrimento devem ser fornecidos no arquivo de critérios.
Comportamento Estrutural – Tipos de Lajes
Os principais efeitos da protensão na laje são a aplicação de uma compressão centrada na laje e uma carga distribuída vertical, geralmente contrária a carga gravitacional. Com isto, as tensões de tração devido ao carregamento externo diminuem sensivelmente e, dependendo do grau de protensão adotado, até se anulam. Normalmente, a protensão é dimensionada apenas para combater uma parte da totalidade das cargas verticais, por exemplo, para combater apenas o peso próprio e/ou cargas quase-permanentes. Com a aplicação da totalidade das cargas acidentais, tensões de tração surgirão e, torna-se importante o cálculo e o controle do grau de fissuração da laje. Como este cálculo de fissuração é feito automaticamente pelo programa, basta variar a intensidade da protensão e verificar seus efeitos nos diagramas de abertura de fissuras.
As estruturas protendidas que sofrem o efeito da aplicação de cargas elevadas deformam, encurtam, fletem, etc. Se a estrutura está totalmente livre para deformar (por exemplo, uma viga bi-apoiada, rotulada nos extremos e podendo se deslocar horizontalmente em um apoio), o efeito da protensão não provoca nenhuma reação dos apoios externos. Caso contrário, isto é, os apoios restringem os deslocamentos da laje submetida apenas a protensão, aparecerão reações de apoio na estrutura. Estes esforços adicionais que os apoios aplicam na estrutura devem ser considerados no projeto como se fossem efeitos secundários devido à protensão. Eles têm um tratamento especial e são, normalmente, denominados de hiperestáticos de protensão. Mais à frente, explicaremos melhor este efeito no modelo estrutural adotado para a laje.
Modelo uni ou bidirecional
Existe certa polêmica no mercado sobre o modelo estrutural a ser adotado para a análise de solicitações de uma laje plana. O modelo pode ser unidirecional ou deve ser bidirecional?
Baseado na influência americana, o modelo mais comum é o unidirecional através da montagem de um pórtico equivalente para cada linha de interesse na laje em cada direção. Entretanto, este modelo possui alguns inconvenientes como: as lajes podem não ter seus apoios dispostos regularmente, podem apresentar vigas internas e de borda, etc. Considerando as facilidades e as ferramentas computacionais hoje encontradas, adotamos para o lajes protendidas o modelo bidirecional.
No modelo unidirecional, entre dois apoios a laje é tratada como tendo um vão livre. No bidirecional, entre dois apoios, a laje é tratada como se tivesse inúmeros vínculos elásticos, representativos da presença da laje na outra direção.
A experiência tem mostrado que o modelo bidirecional acarreta um dimensionamento sensivelmente mais econômico, com reduções de cablagem e de armadura passiva que podem chegar a 20% ou mais com relação às do método simplificado [referência bibliográfica 8].
Experimentações realizadas comprovaram que a presença do cabo na laje não afeta o seu comportamento estrutural a menos da presença das forças de alívio (forças contrária a gravidade que o cabo aplica ao longo da sua extensão no concreto) e das forças de compressão nas ancoragens. Os cabos funcionam então, através destas cargas, como se fossem mecanismos para modificar o modelo estrutural. Em um exemplo simples: com a introdução de um cabo reto e com inflexão no meio da laje, conseguiremos introduzir uma força concentrada de baixo para cima no meio da laje.
Os cabos podem estar dispostos concentrados nos apoios ou distribuídos ao longo da extensão da laje. Em função desta disposição, as forças que o cabo aplica na laje variam. No exemplo abaixo, extraído da referência bibliográfica [7], modelo bidirecional, temos os diagramas de momentos fletores provenientes de diferentes concentrações de cabos nos apoios. Note que os momentos fletores negativos junto aos apoios possuem picos muitas vezes superiores que os picos dos momentos positivos. Observe também a grande variação, na direção transversal, do momento fletor negativo no apoio devido à distribuição dos cabos.
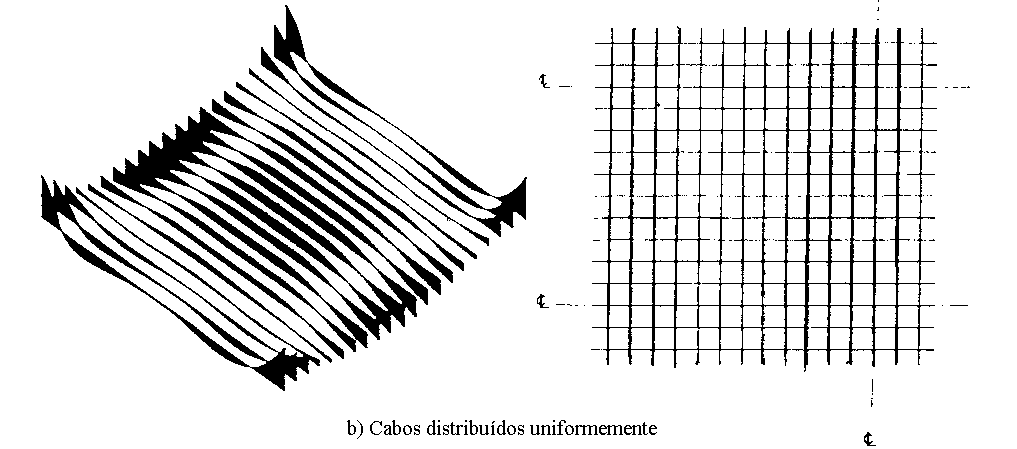
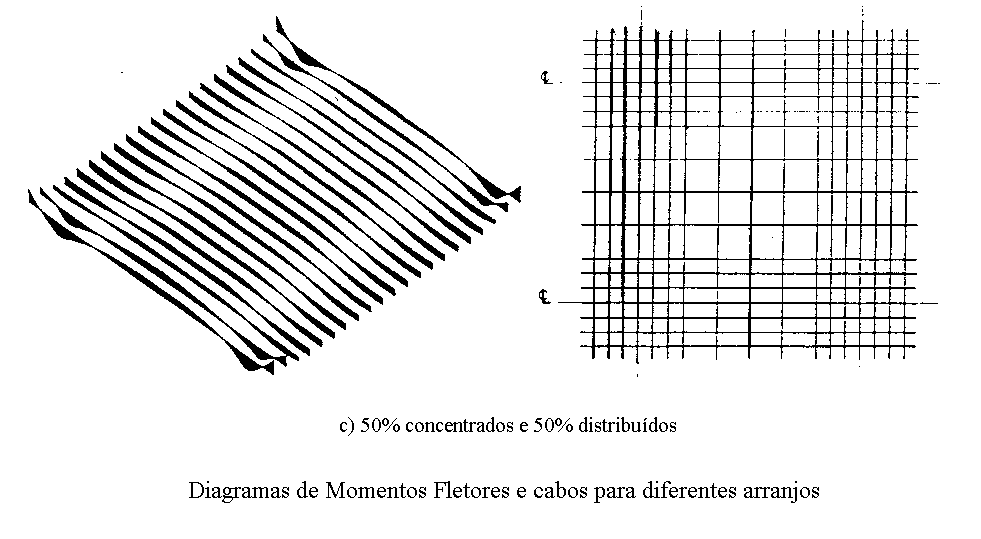
É interessante notar a grande diversidade de valores de momentos fletores, principalmente junto aos apoios, em função da disposição dos cabos. Para o efetivo dimensionamento da laje, os momentos fletores negativos numa determinada região, são adotados como sendo a média dos momentos ao longo de uma faixa, transversalmente.
O modelo unidirecional que trata cada pórtico plano isoladamente conduz, em geral, aos resultados [referência bibliográfica 7]:
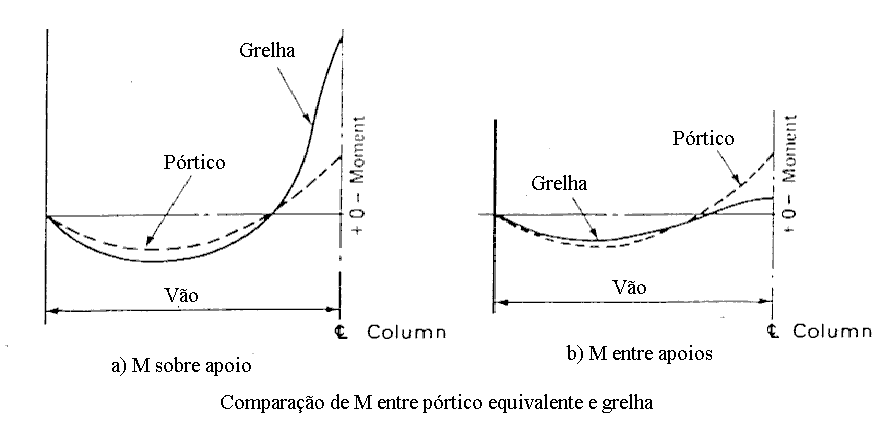
- nas faixas dos apoios, os momentos fletores (-) são muito menores.
- nas faixas dos vãos, os momentos fletores (-) são muito maiores;
- nas faixas dos apoios, os momentos fletores (+) são pouco menores;
- nas faixas dos vãos, os momentos fletores (+) são pouco maiores.
Para não ter que ficar simulando modelos simplificados, considerando a grande variação e influência que a distribuição dos cabos provocam nas solicitações finais, considerando a generalidade do modelo estrutural, etc., adotamos neste sistema de lajes protendidas dois elementos de barra possíveis: barra com 3 graus de liberdade e barra com 6 graus de liberdade. Em ambos os casos, o pavimento é representado por uma grelha de barras.
O elemento de barra com 3 graus de liberdade por extremidade trata apenas cargas normais ao seu plano e não considera o efeito da deformação axial dos elementos.
O elemento de barra com 6 graus de liberdade por extremidade trata de forma abrangente todos os carregamentos na estrutura, normais ou perpendiculares ao plano da laje, considerando também o efeito de deformação axial dos elementos.
O modelo de grelha do pavimento que é gerado para a análise estrutural pode ser analisado isoladamente ou em conjunto com os demais pavimentos do edifício.
Tipos de lajes
Como já partimos de modelos mais gerais para a análise estrutural, os tipos de lajes tratados pelo sistema de "Lajes Protendidas" podem ser:
- Lajes lisas;
- Lajes cogumelo;
- Lajes com vigas de borda e/ou intermediárias;
- Lajes nervuradas em uma ou duas direções (protensão nas nervuras);
- Lajes nervuradas com vigas faixa passando pelos apoios (protensão nas nervuras e/ou nas vigas faixa);
- Lajes lisas, cogumelos e/ou nervuradas com capitéis da altura da laje;
- Lajes lisas, cogumelos e/ou nervuradas com capitéis de altura maiores que a laje.
Para estes tipos de lajes, a geometria da laje pode ser qualquer e com disposições de pilares quaisquer, pois o modelo de grelha que será gerado traduzirá a consideração correta da geometria de todos os elementos.
A presença de furos nas lajes também poderão ser levados em conta no modelo estrutural, pois a discretização do pavimento já elimina as barras presentes nestes furos.
Forças de alívio ou cargas balanceadas
Vamos examinar uma estrutura bem simples: uma viga com dois apoios com restrição apenas na direção vertical submetida a uma carga distribuída "q". O diagrama de momentos fletores é uma parábola de 2° grau, conhecida de todos e o valor máximo deste momento é o valor conhecido M = ql2/8.
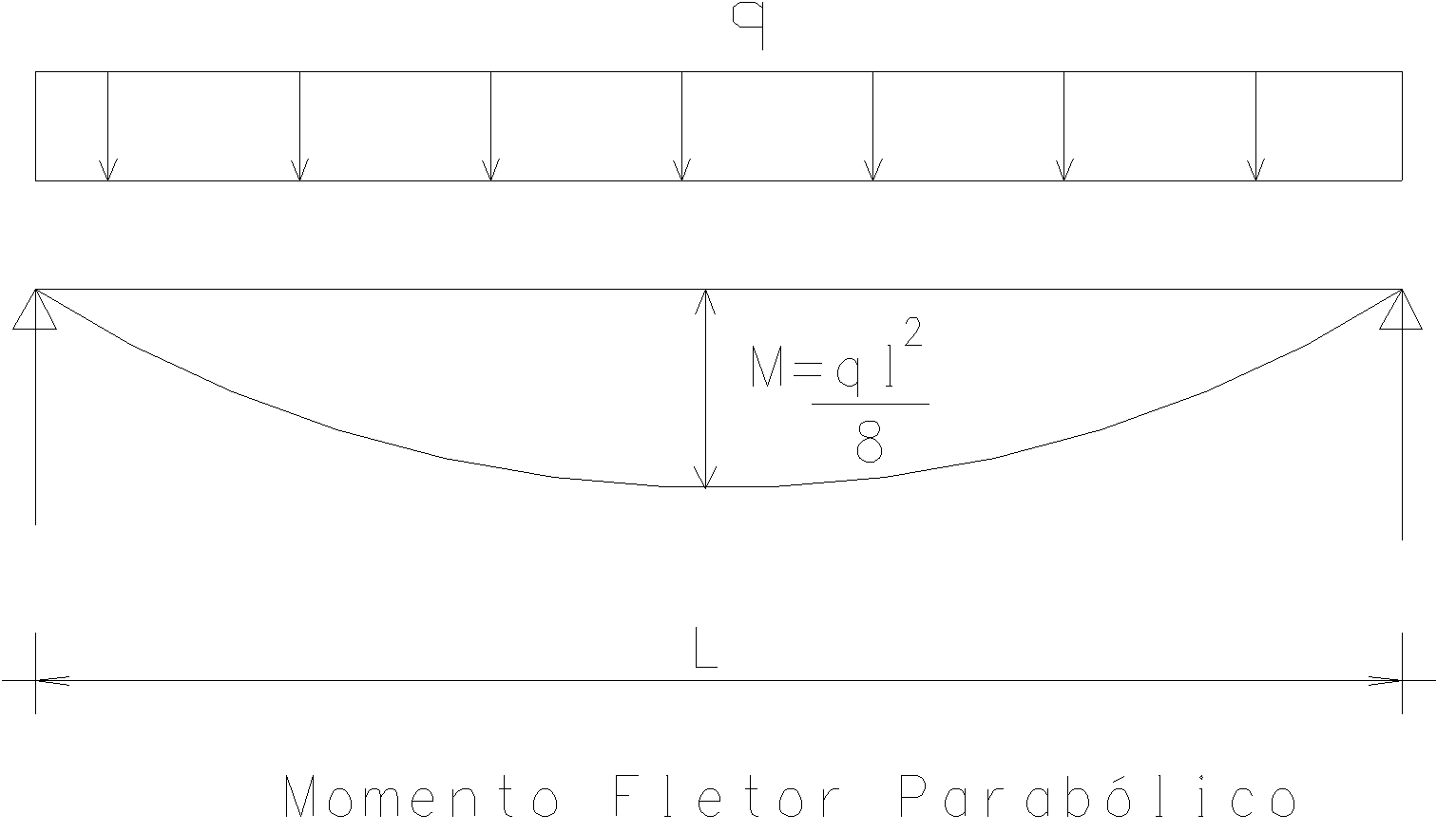
Agora, nesta mesma viga, sem nenhum carregamento, vamos inserir um cabo de protensão como na figura abaixo onde a perfil do cabo ao longo da viga é também uma parábola de 2º grau. A força de protensão é P e a excentricidade máxima no meio do vão é "f" que é um valor definido pela geometria da viga.
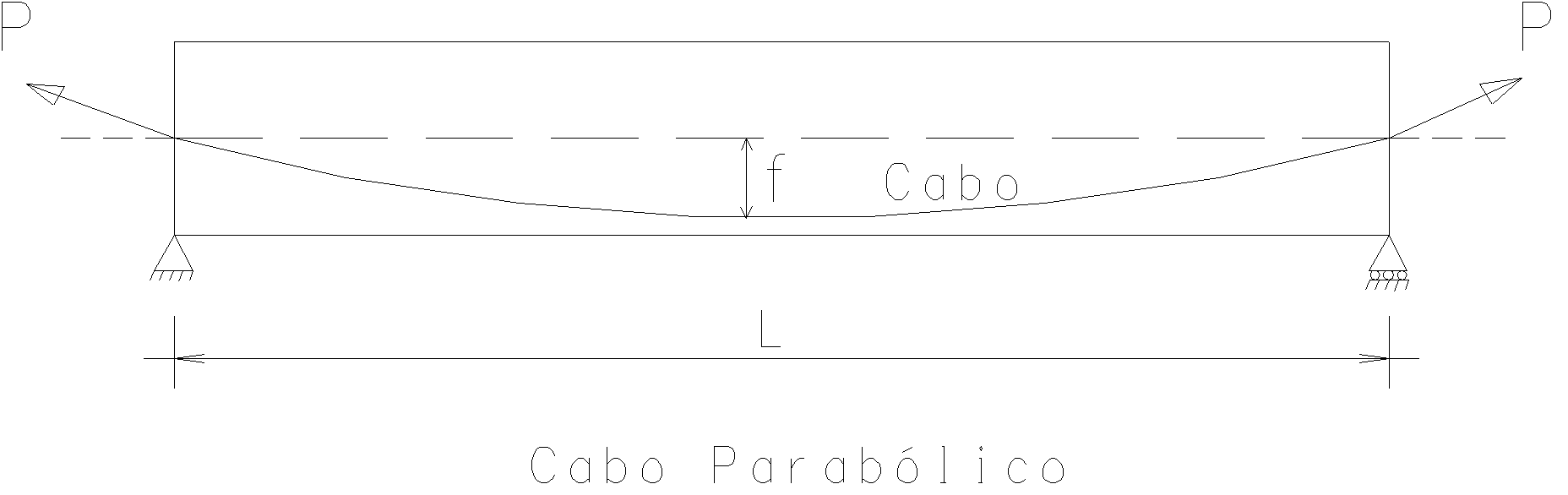
Com isto, introduzimos na viga um momento fletor no meio do vão igual a Pf. Este momento fletor irá variar de acordo com o valor f, sendo nulo nos apoios. No caso de um cabo parabólico, o diagrama de momentos fletores também será parabólico, já que valor de momento depende diretamente de f.
Destas duas figuras surge um princípio básico da protensão: utilizando um cabo parabólico, estaremos aplicando um momento parabólico na viga (ou laje). Isto equivale a dizer que o efeito de um cabo parabólico corresponde a uma carga uniformemente distribuída.
Se igualarmos os valores dos dois momentos teremos o valor da força de protensão que vai provocar na viga uma carga de mesma intensidade da carga vertical "q" e de sentido contrário:
Assim para equilibrarmos uma determinada carga distribuída uniforme correspondente ao peso próprio ou a outra carga permanente qualquer, basta aplicar a força de protensão correspondente P, proporcional a carga a ser balanceada ( "q" ), ao vão ( L ) e a inflexão da parábola.
Este raciocínio é bastante simples para uma viga unifilar, um cabo, uma carga distribuída uniforme, um vão, etc. No caso geral de lajes, temos diversos cabos com diversos perfis, cargas variáveis, tratamento bidirecional, diversos vãos, etc, o que torna a análise geral bastante trabalhosa.
Neste sistema de "Lajes Protendidas", em função das variáveis acima e também da discretização da laje em barras de dimensões finitas, não adotamos o processo analítico para o cálculo das forças de alívio. Adotamos um processo numérico que considera, ao longo de uma determinada direção, as diversas barras da grelha e, para cada extremidade destas barras, temos um momento fletor atuante devido a presença do cabo.
As forças de alívio são calculadas para os extremos destes trechos e integradas em cada nó da grelha para todos os extremos de barras que convergem para este nó. Explicação detalhada e pormenorizada deste processo está explicada na referência bibliográfica [6]. Evidentemente que, quanto maior for a discretização das barras da grelha, maior será a exatidão do processo. Na referência [6] também está explanada toda a justificação teórica deste processo.
O processo numérico é muito vantajoso para a aplicação em programas de computador. Esta é uma das razões pelas quais o sistema de "Lajes Protendidas" consegue tratar os mais diferentes tipos e formatos de lajes de forma eficiente e rápida.
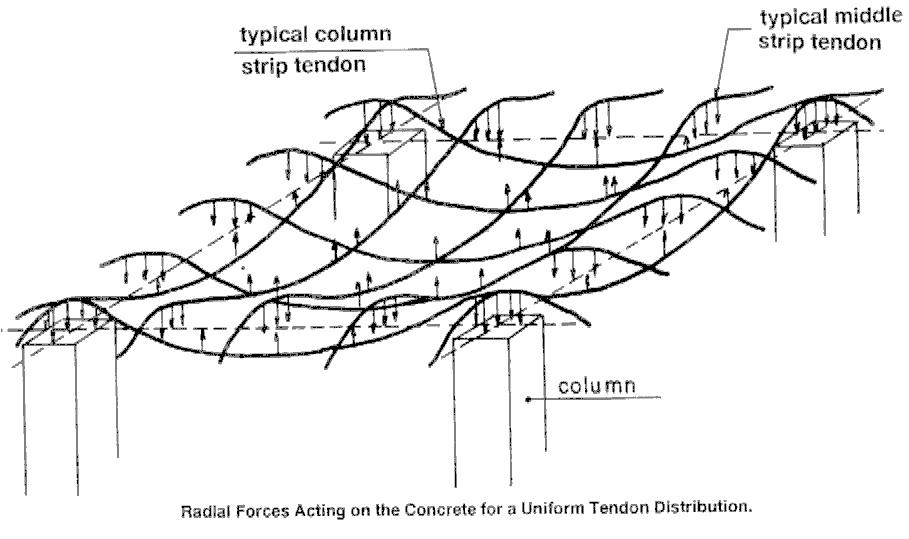
Na figura abaixo, apresentamos um diagrama dos cabos em 3 dimensões com as respectivas forças de alívio. Estas forças distribuídas é que são integradas e aplicadas aos nós do modelo.
Momentos isostáticos e hiperestáticos
O efeito do cabo na estrutura pode ser traduzido por 3 tipos de ações:
- Força axial de compressão: PH
- Momento fletor e força cortante nos extremos: PV , ME , MD
- Forças de alívio: pa
A figura abaixo ilustra estes 3 tipos de ações:

Para pavimentos tratados como pórtico espacial, os esforços normais, momentos fletores e forças cortantes nos extremos são considerados pelo sistema de "Lajes Protendidas" automaticamente. Em geral os cabos entram na laje na horizontal, com ângulo de inclinação igual a zero não introduzindo força cortante.
Vamos tratar com maior detalhe o que acontece com as forças de alívio. Adotaremos o modelo de uma viga com 3 apoios a título de exemplo. A figura abaixo ilustra, esquematicamente esta viga com o traçado do cabo poligonal. Como a viga é contínua, o cabo de protensão tem 5 parábolas internas.
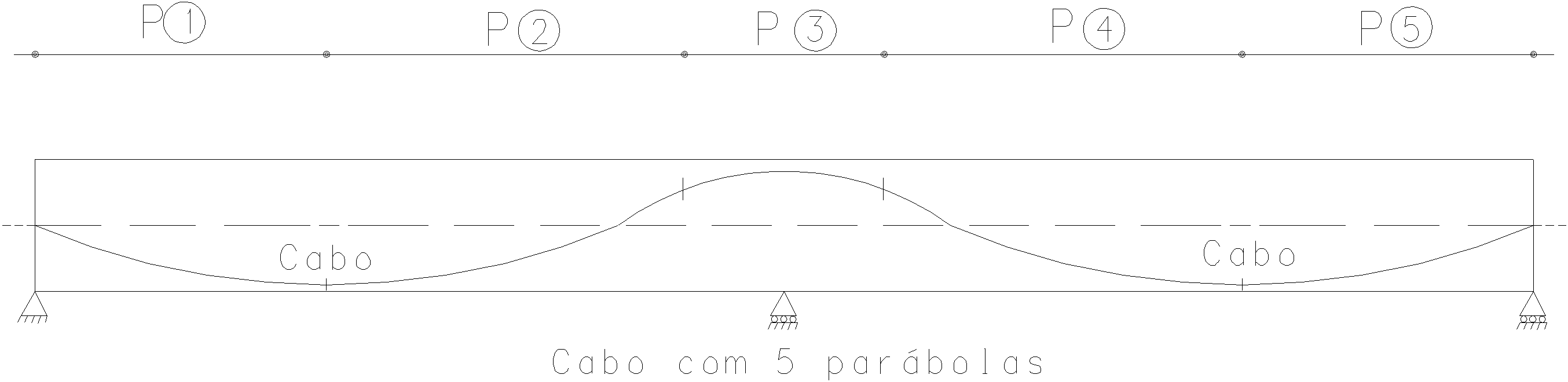
A estes cabos parabólicos tracionados com uma força P, temos as seguintes forças de alívio.
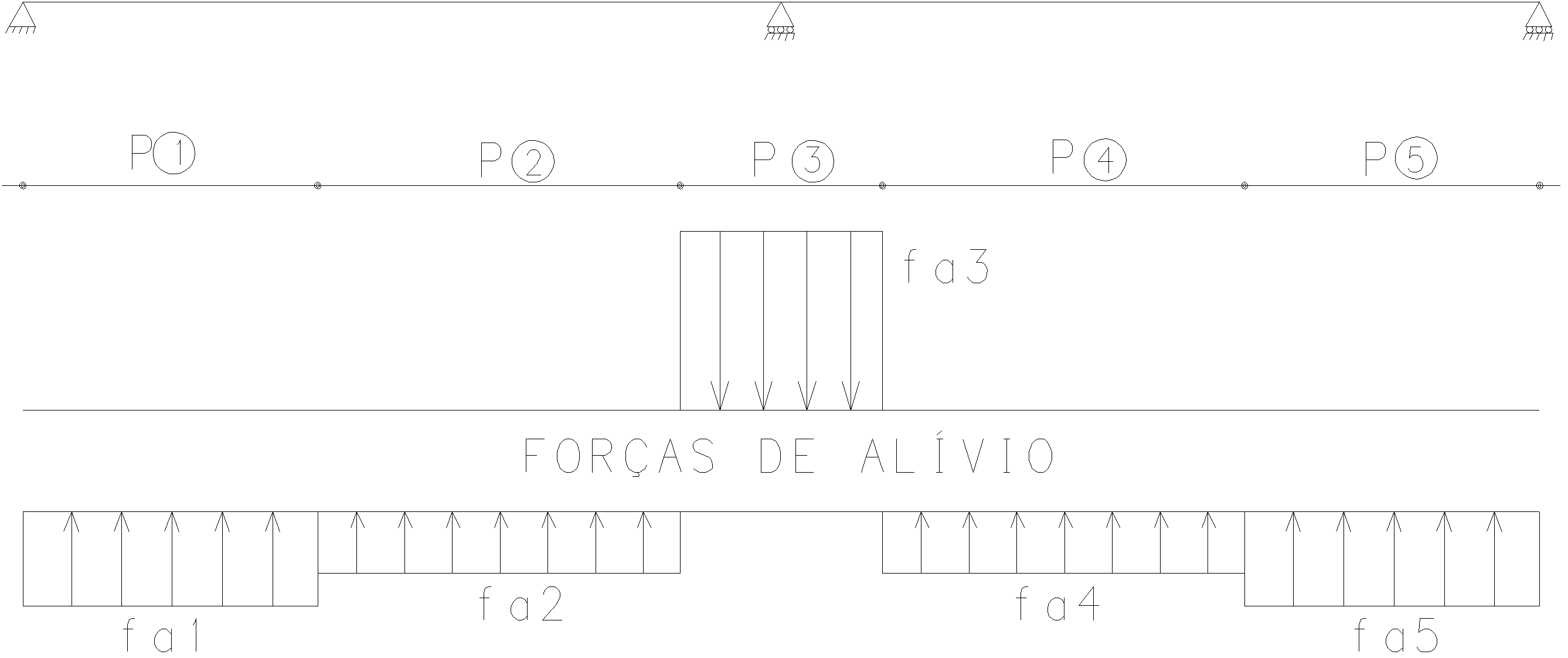
Resolvendo esta viga contínua temos os diagramas de momentos fletores:
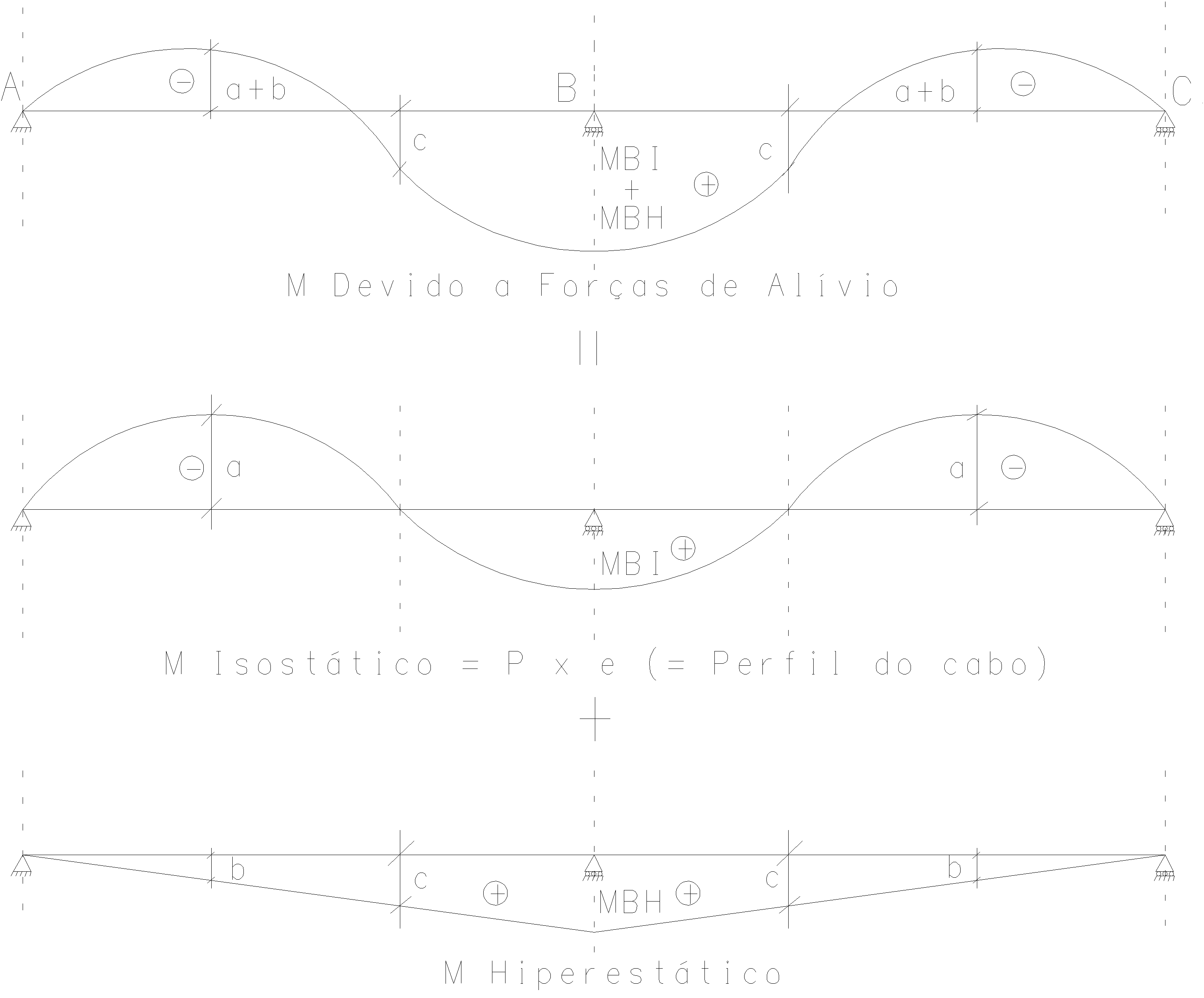
O diagrama de momentos fletores acima é o efeito das cargas verticais do cabo (forças de alívio) na viga. No apoio central da viga temos como resultado um valor Mapoio. Por definição, este Mapoio tem dois componentes básicos:
- Misostático = P x excentricidade no apoio
- Mhiperestático = Mapoio – Misostático
Esta separação é feita por que para o dimensionamento da viga (ou laje) no Estado Limite Último, o Misostático deve ser considerado sem os coeficientes de majoração e contribuindo para a capacidade resistente da seção. Já o Mhiperestático , no Estado Limite Último, é considerado como uma carga externa aplicada (devido as reações aos impedimentos de deslocamento dos apoios) e com seus respectivos coeficientes de majoração.
Em geral, para o Estado Limite de Serviço, estes dois efeitos não necessitam de nenhuma separação.
Evidentemente que os valores do Mhiperestático dependem do perfil do cabo, da intensidade da protensão, geometria da laje, etc. Certas lajes possuem Mhiperestáticos consideráveis, outras não.
O conceito de Mhiperestático é fácil de entender numa estrutura simples como uma viga contínua. Entretanto para estruturas planas (lajes) discretizadas como barras de grelha, este conceito é mais complexo. As barras numa direção, além de se apoiarem rigidamente nos apoios, também se apóiam em vínculos elásticos representados pelas barras da grelha na direção vertical. Há uma grande interação entre as barras da grelha nas duas direções. Este é também um dos fatores importantes para a análise estrutural da laje como modelo estrutural de grelha. Na referência [6] também está explicado com detalhes como ocorre esta interação entre as barras nas duas direções.
Recordando, efetuada a protensão, apenas a atuação das forças de alívio provocaram na estrutura os Misostáticos e Mhiperestáticos . Por definição, os momentos isostáticos são aqueles resultantes unicamente da ação da carga excêntrica na seção. Se a estrutura, sob o efeito das forças de alívio (e também das forças normais de compressão devido ao cabo), tentar se deformar e for impedida no seu deslocamento pelos vínculos existentes, reações de apoio adicionais aparecerão nestes pontos provocando momentos fletores secundários na estrutura que são denominados de Mhiperestáticos.
Estruturas estaticamente determinadas como, por exemplo, balanços e vigas isostáticas, não possuem momentos hiperestáticos.
Para dimensionamento das armaduras passivas, os momentos fletores devido a atuação das cargas externas (peso próprio, permanentes e acidentais) aplicadas são somados aos momentos hiperestáticos.
O sistema de "Lajes Protendidas" já calcula separadamente este Mhiperestático automaticamente e apresenta todos os seus diagramas nas barras da grelha. Também os deslocamentos da laje são devidamente calculados para as forças de alívio e Mhiperestático.
O processo utilizado pelo "Lajes Protendidas" para o Mhiperestático é simplesmente carregar as barras da grelha com as forças de alívio (integradas em cada nó) e também carregar as barras da grelha com os Misostáticos de sinal contrário. Na referência [6] está explanado com detalhes o cálculo destas forças de alívio nos nós. O resultado do processamento fornecerá os Mhiperestáticos.
Com base na experiência de acompanhamento de inúmeros clientes, este é o conceito mais difícil de ser entendido para o projeto de peças protendidas.
Extrapolando este conceito, o mesmo que explicamos aqui para as cargas verticais, também é válido para as cargas horizontais e forças cortantes. As estruturas protendidas que sofrem o efeito da aplicação de cargas elevadas também podem apresentar Nisostáticas e Nhiperestáticas.
Verificação: Estado Limite de Serviço
A verificação estrutural realizada para o Estado Limite em Serviço abrange três condições:
- Deformações ( flechas);
- Tensões;
- Fissuração.
Deformações
Para a verificação das deformações, o sistema de "Projeto de Lajes Protendidas" apresenta graficamente todos os deslocamentos verticais e rotações dos pontos discretizados da grelha. Esta apresentação é feita no plano ou em três dimensões. Os resultados podem ser visualizados ou em perspectiva ou através de curvas de isovalores.
Automaticamente, o sistema já prepara carregamentos para esta finalidade. Basicamente três carregamentos já são montados por ocasião da geração do modelo da grelha com a seguinte finalidade:
- Flechas imediatas logo após a protensão (ato da protensão);
- Flechas imediatas para os carregamentos frequentes;
- Flechas considerando a deformação lenta para os carregamentos frequentes.
Neste último caso, as flechas devido as cargas permanentes e protensão são majoradas do fator 2, de modo a considerarmos de forma aproximada a fluência. Caso se queira um fator de majoração diferente, é necessário alterar este valor na geração de carregamentos do modelo.
Tensões normais
O Sistema de "Lajes Protendidas" adota, em princípio, o dimensionamento de lajes com protensão parcial, devendo ser respeitadas as condições de descompressão para as combinações quase-permanentes e as do estado limite de abertura de fissuras, com wk 0,2mm para as combinações frequentes.
As verificações são realizadas em cada região da laje definida como uma região de protensão uniforme.
No regime elástico linear as expressões utilizadas para cálculo das tensões normais nas fibras extremas da laje (superior ou inferior) são dadas por:
;
onde:
- P – força de protensão (com as perdas imediatas e perdas ao longo do tempo);
- e – distância do ponto de passagem do cabo na seção ao baricentro da laje;
- S – área da seção transversal;
- Wi – módulo de resistência à flexão, inferior, da seção transversal;
- Ws – módulo de resistência à flexão, superior, da seção transversal;
- M – momento externo atuante;
- MH – momento hiperestático;
- HP – coeficiente de majoração do hiperestático de protensão.
Verificação da tensão em utilização
A NBR 6118 não estabelece limitações de tensão para o caso de protensão parcial no estado limite de utilização – ELS (considerando-se a protensão P, após todas as perdas e j > 28 dias). Apesar disto, o sistema de "Lajes Protendidas" permite a definição de limites de tensão, que serão verificados durante o cálculo automático:
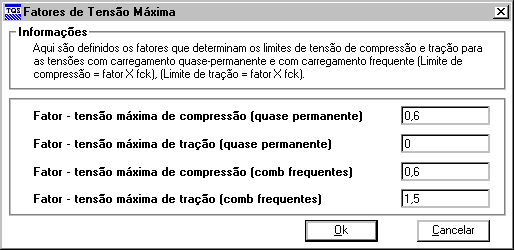
O projetista deve fornecer o valor do fck no arquivo de critérios e também o coeficiente . Além de tais valores, os fatores de multiplicação de tensão também podem ser alterado no arquivo de critérios.
Fissuração
O cálculo da fissuração é realizado para a condição de carregamento frequente. Para o cálculo da fissuração, o "Lajes Protendidas" segue os seguintes passos:
Não ocorre a abertura de fissuras
Se as tensões nas fibras superiores e inferiores da seção forem de compressão, não há a abertura de fissuras e seu valor é assumido como sendo 0.
Com tensão de tração
Neste caso é necessário o cálculo do valor da abertura de fissuras. A NBR 6118 (item 13.4.2) considera que a fissuração é nociva quando a abertura das fissuras na superfície do concreto ultrapassa o valor .
A NBR 6118, item 17.3.3.2 apresenta um método para estimativa dos valores característicos das fissuras, que leva em conta a área de envolvimento de cada uma das armadura, sendo apresentadas as seguintes expressões e adotado o menor valor entre as duas:
onde:
- i – diâmetro da armadura i, que protege a região de envolvimento Acri;
- si – tensão de tração no centro armadura i, calculada no Estádio II. Nos elementos protendidos, o valor de si é o acréscimo de tensão entre o estado limite de descompressão (antigo estado convencional de neutralização) e o estado de carregamento considerado; neste cálculo será levada em conta a totalidade da armadura de tração, inclusive os cabos que estejam em bainha;
- ri – taxa de armadura (passiva ou protendida que não esteja em bainha) em relação a respectiva área de envolvimento Acri ;
- Acri – área da região de envolvimento de concreto protegida pela armadura i e constituída por um quadrado de lados 15i ;
- Esi – módulo de elasticidade do aço da armadura i.
O equilíbrio da seção transversal no Estádio II é representada conforme a fig. abaixo [referência bibliográfica 1]:
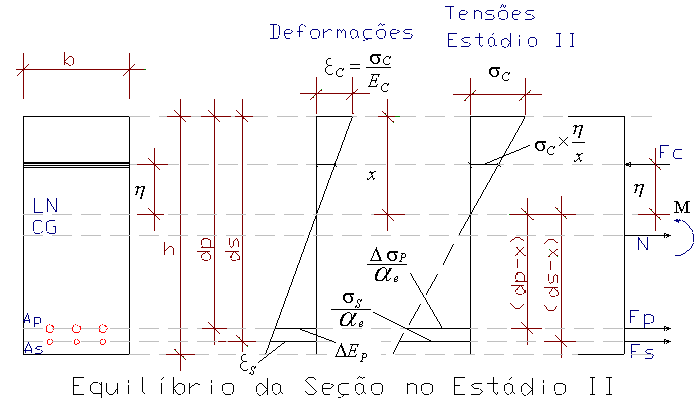
Impondo o equilíbrio das forças normais e dos momentos fletores chegamos as seguintes equações:
onde:
- N – força normal;
- M – momento fletor;
- h – altura da seção de concreto;
- Fc – força normal de compressão - concreto;
- Fs – força normal de tração - armadura passiva;
- Fp – força normal de tração - armadura protendida;
- x – profundidade da linha neutra da seção;
- dp – profundidade do baricentro da armadura protendida;
- ds – profundidade do baricentro da armadura passiva;
- – distância entre Fc e a linha neutra da seção.
Trabalhando com as duas equações acima chegamos a expressão (equação de terceiro grau) que correlaciona o valor de x (profundidade da linha neutra) e Ep (deformação do aço de protensão).
Resolvendo esta equação pelo método de Newton-Raphson, chegamos ao valor de σs (tensão do aço de protensão) desejado.
Dimensionamento ao Estado Limite Último
Os estados limites últimos devidos a solicitações normais são verificados no ato da protensão e no tempo infinito. Vamos apresentar como esta verificação é realizada em cada caso:
Solicitações Normais – Ato da Protensão
A verificação no estado limite último de ruptura no Ato da Protensão é realizado pelo cálculo das tensões normais na borda superior e borda inferior como abaixo:
;
onde:
- P – força de protensão (apenas com as perdas imediatas);
- e – distância do ponto de passagem do cabo na seção ao baricentro da laje;
- S – área da seção transversal;
- Wi – módulo de resistência à flexão, inferior, da seção transversal;
- Ws – módulo de resistência à flexão, superior, da seção transversal
- M – momento externo atuante devido ao carregamento definido como "atopro";
- MH – momento hiperestático;
- P – coeficiente de majoração da força de protensão;
- f – coeficiente de majoração das forças;
- HP – coeficiente de majoração do hiperestático de protensão.
Considerando-se a ativação da protensão P0 (sem consideração de perdas) aos j dias de idade do concreto e as ações permanentes mobilizadas (peso próprio), as tensões normais na seção mais solicitada, determinadas em regime elástico linear, devem atender as seguintes condições:
- borda comprimida: c 0,7 * fckj
- borda tracionada: t 1,2 * fctmj
O projetista deve fornecer os valores de fckj, fctmj e os coeficientes de majoração e no arquivo de critérios. Além de tais valores, os fatores 0,7 e 1,2, multiplicadores para as tensões de compressão e tração, também podem ser alterados no arquivo de critérios.
Por fim, também é calculada a armadura passiva necessária se existir tensão de tração no ato da protensão.
Solicitações Normais - Tempo Infinito
Para verificar se armaduras de protensão dispostas na faixa atendem aos critérios do ELU de ruptura ou de deformação plástica excessiva, o programa utiliza um processo numérico para o tratamento da seção transversal de forma retangular ou "T".
O momento solicitante total atuante é considerado como sendo:
As hipóteses básicas para este dimensionamento da seção são:
- As seções transversais após a flexão permanecem planas;
- A resistência do concreto a tração é desprezada;
- A deformação total da armadura de protensão é tomada considerando-se o alongamento prévio correspondente ao valor representativo da força de protensão (pré-alongamento εpi);
- O alongamento máximo da armadura mais tracionada é assumido como 0.01. Este alongamento é o correspondente além do pré-alongamento;
- O encurtamento máximo na borda extrema do concreto é:
- 0.0035 na flexão simples e composta;
- 0.002 em compressão centrada;
- Os diagramas tensão / deformação do concreto, do aço convencional e do aço de protensão são os apresentados na NBR 6118, itens 8.2, 8.3 e 8.4.
- O processo adotado pelo sistema de "Lajes Protendidas" é um processo numérico interativo. Ele é válido para seções transversais quaisquer. Os seguintes passos são adotados:
- A seção transversal de concreto é discretizada em pequenos retângulos. Atualmente esta discretização é realizada para a secção retangular e T;
- A armadura de protensão é considerada na sua posição exata;
- A posição da armadura convencional é considerada na borda da seção mais tracionada descontando-se o valor do cobrimento e/ou bitola adotada;
- Adota-se inicialmente um valor mínimo para a armadura convencional;
- Em seguida é assumida uma posição e uma inclinação da linha neutra para a seção;
- Através de um processo de convergência baseada no método de Newton-Raphson a duas variáveis, tenta-se encontrar uma linha neutra de equilíbrio entre as solicitações externas e internas conforme figura abaixo:
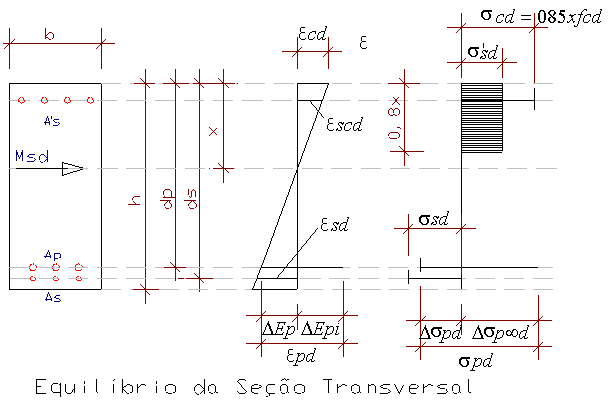
- Não encontrada solução possível, o valor da armadura convencional é incrementada até que uma solução de equilíbrio seja encontrada;
- A condição de segurança quanto ao ELU do concreto ou deformações excessivas da armadura, é considerada convencionalmente atingida quando a deformação da seção não apresentar, na representação da figura abaixo, nenhum ponto externo à região contornada pela poligonal AFBCDEA [referência bibliográfica 1].
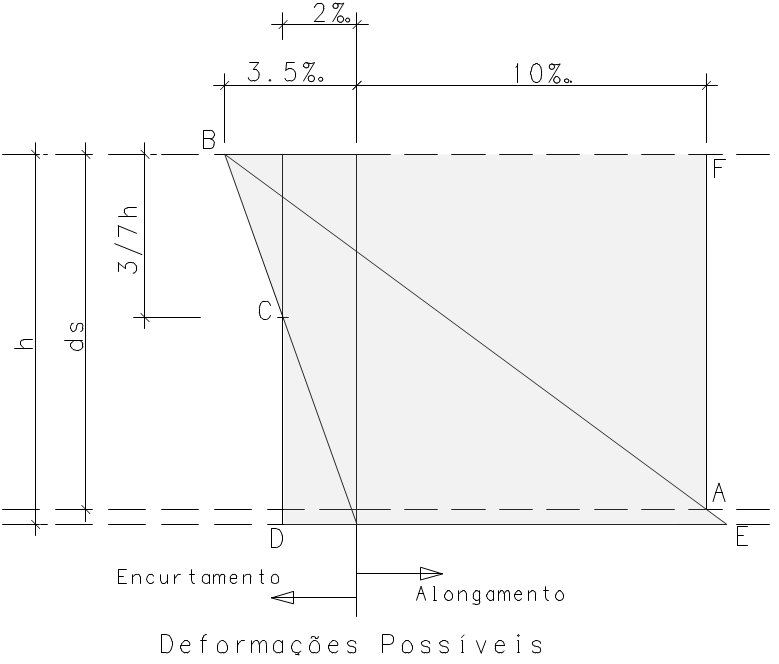
Para o dimensionamento da seção com cordoalhas aderentes, o aço de protensão é considerado como participando efetivamente da resistência da seção pois sua deformação acompanha exatamente a deformação da seção.
Para o dimensionamento da seção com cordoalhas engraxadas, o aço de protensão se deforma diferente da seção transversal de concreto porque ele não é aderente ao concreto. Podem ser utilizadas as expressões da NBR 6118, item 17.2.2.c para determinação do acréscimo de tensão de estruturas que utilizem armaduras ativas não aderentes ou definidos valores fixos no arquivo de critérios.
O valor de armadura mínima passiva também é verificada, de acordo com o item 19.3.3.2 da NBR6118:2003.
Perdas de Protensão
As perdas de protensão podem ser classificadas em dois tipos principais:
- Perdas Imediatas;
- Perdas Retardadas.
Vamos analisar cada um destes tipos de perdas e entender como o "Lajes Protendidas" os trata.
Perdas imediatas
As perdas que ocorrem imediatamente no ato da protensão dos cabos são divididas em três categorias diferentes:
Perdas devido à deformação elástica do concreto
Quando os cabos são estirados, os macacos se apoiam diretamente no concreto e o encurtamento elástico se realiza antes da ancoragem do cabo. Sendo assim, nas peças onde a protensão dos cabos é executada em uma única operação, não existem perdas por deformação imediata a serem consideradas.
Perda por atrito
Por estar alojada numa bainha de traçado normalmente curvo, a armadura de protensão ao se deslocar devido à força aplicada em suas extremidades, produz atrito entre o cabo e a bainha, que é inevitável.
Em função do coeficiente de atrito e das forças de inflexão Pi, os esforços ao longo da armadura poderão ser quantificados, considerando-se o efeito das forças de atrito atuantes. As perdas por atrito são determinadas pela expressão:
Onde:
- P(x) − perda da força de protensão no cabo na seção de abscissa x;
- Pi − força aplicada a armadura de protensão pelo equipamento de tração;
- − soma dos ângulos de desvio previstos, no trecho compreendido entre as abscissas 0 e x ;
- − coeficiente de atrito aparente entre cabo e bainha;
- k − coeficiente de perda por metro provocada por curvaturas não intencionais do cabo.
Perdas por acomodação da ancoragem
Durante o processo de cravação das cunhas dos dispositivos de ancoragem, ocorre um recuo da armadura, que introduz novas perdas da força de protensão. Na maioria dos sistemas de protensão, a cravação das cunhas se dá por atrito entre estas e a armadura. Este atrito faz com que o efeito do recuo das ancoragens só se faça sentir dentro de um trecho do cabo definido pela ancoragem e um ponto interno de repouso que deve ser determinado, onde a partir do qual deixa de existir o decréscimo de protensão. Graficamente temos:
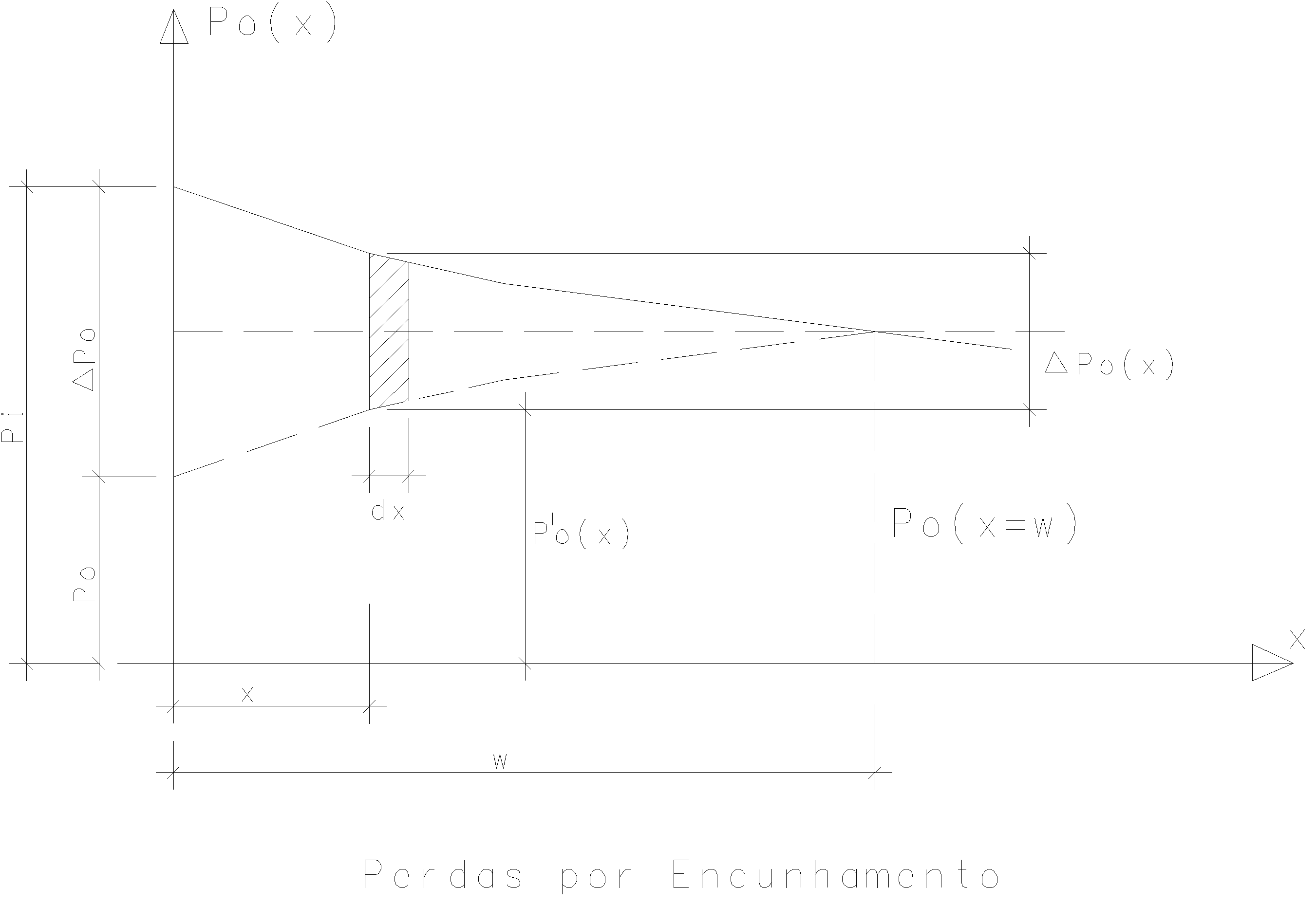
Este ponto de repouso e as correspondentes perdas são determinadas a partir da condição de compatibilidade geométrica: o encurtamento do cabo representado por perdas de tensões é equivalente ao deslocamento (escorregamento) ocorrido W.
Onde:
- = área limitada pela curva (ou reta) de P0(x) durante o estiramento e pela curva ( ou reta) simétrica de P0 (x) durante a volta;
- W = abscissa do ponto de equilíbrio, calculada caso a caso;
- W = deslocamento de encunhamento;
- Ep Ap = rigidez axial do cabo.
Perdas retardadas (lentas)
Estas perdas são representadas pelos seguintes efeitos:
- Retração;
- Deformação Lenta;
- Relaxação do Aço.
Estes três efeitos não são calculados automaticamente pelo "Lajes Protendidas". No arquivo de critérios, este valor de perda deve ser especificado como se fosse uma porcentagem. Para obtenção do valor da força de protensão no tempo infinito o "Lajes Protendida" subtrai do valor da força inicial de protensão, após o computo das perdas imediatas, este valor de perda fornecido.
O Projeto de Protensão
O TQS-Lajes analisa lajes onde é admitida a presença de rebaixos, capitéis e a existência de vigas nas mesmas. Com relação à disposição dos cabos de protensão em planta, ela pode ser paralela a um dos eixos da laje, X ou Y ou então "desviada" acompanhando uma linha poligonal.
Os cabos podem ser tracionados por uma borda apenas (direita ou esquerda), simultaneamente pelas duas bordas ou de forma de alternada.
Descreveremos as etapas envolvidas num "Projeto de Lajes Protendidas" no TQS-Lajes. Em seguida, abordaremos o modelo de cálculo e apresentaremos o conceito de região de protensão uniforme (RPU) e região de transferência de esforços (RTE) .
Etapas do projeto
São as seguintes as etapas envolvidas num "Projeto de Lajes Protendidas" desenvolvido através do TQS-Lajes:
- definição da forma, onde são definidos a distribuição, dimensões e orientação dos pilares e escolhida a espessura da laje;
- especificação dos materiais a serem empregados (aços e concreto);
- definição dos diferentes casos de carregamentos atuantes sobre a laje;
- discretização da laje através de elementos de grelha;
- cálculo dos deslocamentos e esforços solicitantes, sem a consideração da protensão;
- definição e/ou edição das variáveis contidas no arquivo de critérios de protensão;
- determinação de regiões (em planta) delimitadas por linhas poligonais que possuirão a mesma protensão;
- dimensionamento da protensão que abrange a definição do número, da bitola e do traçado dos cabos em elevação, além de sua distribuição em planta;
- cálculo dos efeitos (momentos) hiperestáticos da protensão;
- verificação do atendimento das seguintes condições: tensões admissíveis no ato da protensão; estado limite de abertura de fissuras para a combinação freqüente de ações; estado limite último à solicitações normais que corresponde ao cálculo da armadura passiva necessária à flexão;
- detalhamento da armadura passiva relativa à flexão e ao puncionamento;
- geração dos desenhos dos cabos em planta e em perfil;
- cotagem dos cabos para verificação de interferências;
- extração de lista de cabos de protensão e armadura convencional.
Modelo de cálculo
O módulo de protensão de lajes do sistema TQS-Lajes adota o modelo de grelha (barras com 3 graus de liberdade) ou de pórtico espacial (barras com 6 graus de liberdade) na análise estática das lajes protendidas. Além disso, o modelo do pavimento pode ser analisado isoladamente ou juntamente com os demais pavimentos (modelo estrutural único).
A determinação dos deslocamentos, esforços e reações, resultantes da aplicação das diversas combinações de carregamento sobre a laje, é realizada através de tal modelo, supondo-o com comportamento elástico linear. Cabe lembrar que os elementos tipo grelha não trabalham a compressão/tração, consequentemente o modelo adotado não leva em conta forças normais aplicadas no plano da laje. A utilização do modelo de pórtico espacial permite esta consideração.
Partindo-se de um espaçamento padrão fornecido pelo projetista, a discretização da laje é realizada automaticamente. Nessa discretização o sistema busca orientar os elementos de barra (de grelha ou pórtico) segundo os eixos X e Y da laje. Deste modo, quase todas as barras podem ser classificadas como horizontal, paralela ao eixo X da laje, ou como vertical, paralela ao eixo Y da laje. No processo de discretização da malha pode ser gerado um pequeno número de barras oblíquas com relação aos eixos X e Y.
O programa possui recursos que possibilitam a simulação de plastificação em barras e em regiões da laje, o que permite uma análise melhorada, em relação à análise elástico linear básica. Além desses recursos o programa também permite que, durante as fases de lançamento de cabo e de verificações, o projetista edite os diagramas de momentos resultantes da análise do modelo estrutural, corrigindo distorções decorrentes do modelo que julgue existir.
Em nossa opinião, a adoção do modelo de grelha/pórtico para a análise de lajes representa um grande avanço com relação à modelagem por faixas, utilizada por algum tempo em alguns escritórios de projetos. Nesse modelo de cálculo a laje é representada em cada sentido por uma viga apoiada sobre as linhas de apoio, que certamente é um modelo pobre, mesmo para lajes não muito complexas.
Define-se como alinhamento de barras uma sequência ordenada de barras com mesma orientação e conectadas entre si através dos seus nós.
Regiões de Protensão Uniforme (RPU) e Regiões de Transferência de Esforços (RTE)
No módulo de lajes protendidas do TQS-Lajes é utilizado o conceito de região de protensão uniforme (RPU) e região de transferência de esforços (RTE) para o lançamento da cablagem e para a verificação e o dimensionamento à flexão da laje.
Define-se como RPU uma região poligonal da laje para a qual são adotados iguais espaçamento, diâmetro, força de protensão e traçado para todos os cabos contidos na mesma.
Define-se como RTE uma região poligonal da laje, que contém uma ou diversas RPU’s e que determinam a região para a extração das solicitações (momentos fletores) para as RPU’s e as dimensões da seção transversal que serão empregadas no dimensionamento.
Basicamente, as RPU’s determinam a região para o desenho dos cabos e a RTE determina a região de influência da protensão contida nas diversas RPU’s que pertencem a esta RTE. Todas as áreas da laje a serem protendidas devem ser abrangidas por RTEs e (ou) RPUs. Os cabos de protensão são distribuídos paralelamente a um dos lados da RPU ao qual é associada.
Para cada RPU podemos ter apenas um traçado de cabo, além disto, o cabo deve iniciar no começo da RPU e terminar no fim da RPU.
Quando uma RTE possui diversas RPU’s, para cada RPU é necessário a definição da porcentagem que servirá de base para a transferência dos esforços solicitantes e da geometria para o dimensionamento de cada RPU. Com isto, podemos ter uma região da laje onde desejamos extrair solicitações comuns para diversos traçados e/ou quantidades de cabos representados por diversas RPUs. Assim, podemos reforçar com alguns cabos um vão extremo onde o momento fletor é maior que os demais vãos, "morrer" com cabos na parte interna do pavimento, etc.
Deste modo, no TQS-Lajes a definição dos cabos de protensão implica numa definição anterior, a da geometria das RTEs e RPUs. Todos os cabos têm que pertencer a alguma RPU e só podem ser lançados com orientação paralela ao traçado da RPU.
Para os propósitos de lançamento dos cabos, de verificações e de dimensionamento cada RPU e RTE é considerada como isolada das demais. Assim, para tais propósitos, as RPUs / RTEs são tratadas como se fossem elementos lineares. E o momento fletor que se supõe atuar em cada seção transversal da mesma é definido a seguir.
Cada RTE pode abranger vários alinhamentos de barras do modelo de grelha com direção idêntica à sua. Os esforços numa dada seção transversal de uma RTE são aproximados de forma discreta pelos seus respectivos valores nos eixos das barras que compõem essa seção. Dependendo da estrutura, tais valores podem apresentar uma grande variação ao longo de uma seção transversal.
No tratamento de uma seção transversal de uma RTE, o TQS-Lajes considera, para cada carregamento ou combinação, a envoltória dos esforços atuantes nos diversos alinhamentos de barras abrangidas pela mesma. Calculada essa envoltória, o valor do esforço utilizado para o lançamento do cabo e nas verificações em uma dada seção transversal da RTE poderá ser:
- a média aritmética entre o máximo e mínimo nessa seção;
- o esforço de maior módulo.
Dentro do arquivo de critérios o engenheiro deverá definir qual o tipo de valor que deverá ser utilizado para os momentos fletores positivos e para os momentos fletores negativos.
O programa também trabalha com RPUs / RTEs de altura variável ao longo do vão.
