Hiperestático de Protensão
Método de Cálculo
Existem pelo menos três formas de se representar a protensão em um elemento de concreto:
- como um conjunto de deformações iniciais;
- como um conjunto de esforços solicitantes iniciais equivalentes;
- como um conjunto de cargas externas equivalentes.
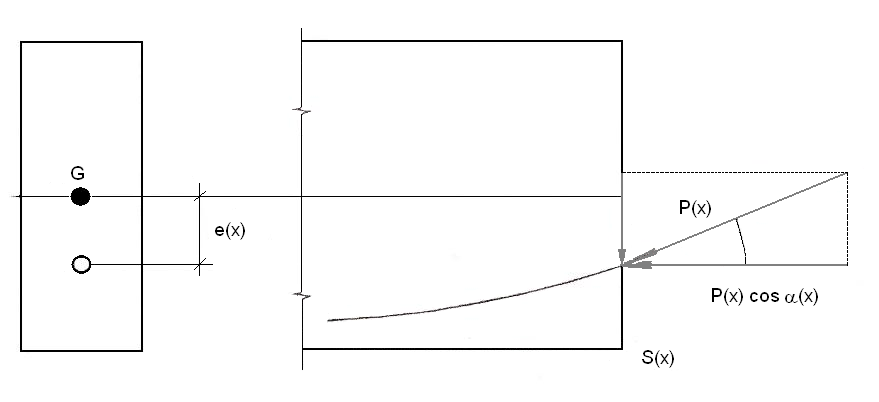
Na segunda forma, o efeito da protensão em qualquer seção S(x) da viga é representado pela força de compressão P(x) do cabo sobre a mesma. Essa força corresponde aos esforços solicitantes:
N(x) = - P(x) . cosα(x) (normal)
V(x) = P(x) . sen α(x) (cortante)
M(x) = - P(x) . e(x). cosα(x) (momento)
No caso de elementos com cabo de protensão de traçado muito abatido, i.e. |α(x)| ≈ 0 para x, tem-se:
N(x) ≈ - P(x)
V(x) ≈ 0
M(x) ≈ - P(x) . e(x)
O método implementado no TQS parte das expressões simplificadas acima para representar, de forma discreta, a protensão em lajes protendidas. Considere-se o caso de um elemento prismático de material elástico linear protendido através de um cabo com um traçado qualquer, que esteja suficientemente apoiada para que não sofra movimentos de corpos rígidos.
Assumindo-se a hipótese das seções planas de Navier-Benoulli, a ação do cabo de protensão em cada seção transversal desse elemento pode ser representada por uma força normal a seção e um momento em relação ao seu centro de gravidade.
Deste modo, teoricamente a protensão do elemento poderia ser considerada impondo-se em cada seção transversal esforços normais e fletor iguais às correspondentes ações exercidas pelo cabo. No entanto, na prática, isto não é possível devido ao fato do número de seções transversais de qualquer viga ser infinito.
O que o método propõe, então, é que se discretize a peça em elementos e considere-se que ao longo de cada elemento a ação do cabo seja constante e igual à atuante no seu ponto médio. Tal hipótese equivale a se adotar um cabo reto com excentricidade e força de protensão constantes para cada elemento da discretização.
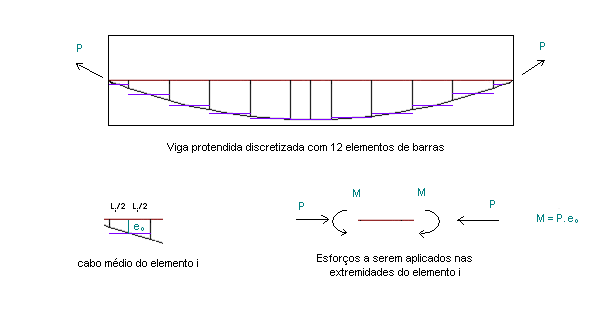
Obviamente, esse método funciona de maneira exata para o caso de elementos com cabos de protensão retos com excentricidade constante. Nos casos de cabos com traçados quaisquer, no limite, quando o número de elementos da discretização tender para o infinito, a solução do método tenderá para a resposta "exata".
Esse método é de fácil implementação computacional. Ele também é muito adequado para o caso de análise de lajes protendidas modeladas como grelha pelos seguintes motivos:
- a pequena grandeza relativa da altura das lajes impõe o lançamento de cabos de protensão com traçados abatidos;
- a geração do modelo de grelha, em geral, envolve uma discretização com grande número de elementos.
Esses dois fatos fazem com a aproximação do método, representada pela adoção de um cabo reto com excentricidade constante ao longo de cada elemento, seja suficientemente precisa no tratamento de lajes protendidas discretizadas como grelha.
Exemplos de Vigas
A seguir serão mostrados vários exemplos que ilustram o funcionamento do método Sérgio Pinheiro/TQS (SP/TQS). Os resultados obtidos através do mesmo serão comparados com resultados obtidos usando-se os métodos da carga equivalente (CE) e das forças de desviação (FD). Será mostrado que o método apresenta praticamente a mesma convergência do método das forças de desviação.
Um aspecto importante do método, que o difere dos outros 2 métodos, é que o momento fletor obtido é o momento hiperestático.
Viga bi-apoiada protendida com um cabo reto
Neste exemplo, figura 1, uma viga bi-apoiada de seção retangular protendida com um cabo reto será analisada através dos métodos da carga equivalente (CE) e do método Sérgio Pinheiro/TQS (SP/TQS).

- l = 10m
- b = 0.25m ; h=0.40m
- E = 100.000 tf/m2
- Fp = 3 tf ; e =
Esta viga foi discretizada em 12 elementos. Nos extremos e no centro a discretização da viga é mais refinada. Nessas regiões os elementos têm 0,5m de comprimento. Nas demais regiões a viga é discretizada com elementos de 1,0m. Na verdade, neste exemplo os resultados de ambos métodos independem da discretização e poderia se chegar à resposta "exata" discretizando-se a viga com apenas 1 elemento .
Os diagramas de momentos fletores da viga estão ilustrados nas figuras a seguir.

Fig.2 – diagrama de momento - método cargas equivalentes (C.E)

Fig. 3 – diagrama nulo de momento - método SP/TQS
Viga com 2 vãos iguais protendida com um cabo reto
Na viga do exemplo anterior é introduzido um terceiro apoio no meio do vão a fim de torná-la hiperestática. A discretização é mantida a mesma e novamente é irrelevante para ambos os métodos.
Os diagramas de momentos fletores da viga estão ilustrados nas figuras a seguir.
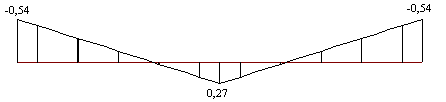
Fig. 4 – diagrama momento cargas equivalentes (CE)
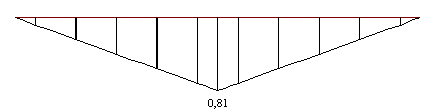
Fig. 5 – diagrama momento método SP/TQS
Note-se que o diagrama do Método da Carga Equivalente (CE) representa o momento total e o diagrama do Método Sérgio Pinheiro o momento hiperestático. A diferença entre os dois diagramas produz um diagrama de momento constante igual ao momento isostático de protensão, como pode ser observado na figura a seguir:

Fig. 6 – diagrama resultante (CE – SP/TQS)
Viga com 2 vãos iguais protendida com cabo parabólico
Na viga do exemplo anterior o cabo reto é substituído por cabo de traçado parabólico com excentricidades nulas nos apoios extremos e máxima, e = 0.18cm, em cima do apoio interno. A força de protensão continua sendo igual a 3 tf. A discretização da viga também é mantida a mesma dos exemplos anteriores.
Neste exemplo, o grau de refinamento da discretização é fundamental para o método SP/TQS e irrelevante para o método das cargas equivalentes (CE). Na verdade, a discretização utilizada nos 3 primeiros exemplos deste trabalho foi definida de tal modo que o método SP/TQS pudesse apresentar resultados precisos no exemplo corrente.
Cabe ressaltar que, obviamente, este exemplo não faz sentido na prática. A intenção em apresentá-lo é apenas de comprovar a eficiência do método proposto através de um exemplo simples, cujo resultado é facilmente calculado através do método das cargas equivalentes.
Os diagramas de momentos fletores da viga estão ilustrados nas figuras a seguir.

Fig. 7 – diagrama momento cargas equivalente (CE)
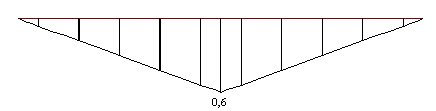
Fig. 8 – diagrama momento método SP/TQS
Note-se que o diagrama do método da carga equivalente representa o momento total e o diagrama do método SP/TQS o momento hiperestático. A diferença entre os dois diagramas produz o diagrama do momento isostático de protensão, como pode ser observado na figura a seguir:

Fig. 9 – diagrama momento resultante
Para efeito de comparação, os valores dos momentos de protensão isostáticos (Mo) nos pontos coincidentes com os nós extremos dos elementos da discretização são apresentados lado a lado a aqueles obtidos no diagrama 9 (CE – SP/TQS):
| Coord . X (m) | Mo (tf.m) | M – CE - SP/TQS (tf.m) |
| 0,0 | 0,000 | 0,000 |
| 0,5 | -0,103 | -0,102 |
| 1,5 | -0,275 | -0,275 |
| 2,5 | -0,405 | -0,404 |
| 3,5 | -0,409 | -0,409 |
| 4,5 | -0,535 | -0,533 |
| 5,0 | -0,540 | -0,538 |
Observa-se através dos valores da tabela acima que o método apresenta resultados bastante próximos dos resultados do método da carga equivalente com a discretização empregada.
Grelha com 2 vigas protendidas proposta pelo prof. Evandro Duarte
Este exemplo foi proposto pelo prof. Evandro no trabalho intitulado "Cálculo Completo de uma Viga Isostática Protendida". Naquele trabalho, o exemplo mostrado na fig. 10 foi analisado pelo Método da Forças de Desviação (FD).
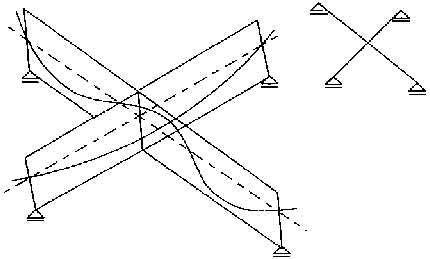
Fig. 10 – Grelha Prof. Evandro Duarte
Neste exemplo, a discretização adotada para a viga de 4m, protendida através de um cabo de traçado parabólico, é a mesma do trabalho do Prof. Evandro: 8 elementos com comprimento igual a 0,5m. Já para a viga de 12m, protendida com um cabo cujo traçado é composto por 3 arcos parabólicos, partiu-se da discretização adotada no trabalho do Prof. Evandro, discretização uniforme com elementos de 1m, e sub-dividiu-se os 2 elementos centrais em 4 elementos de 0,5m. Essa discretização da estrutura é utilizada tanto na análise pelo método SP/TQS como na análise pelo método das forças de desviação.
Os diagramas de momentos fletores da maior viga (vão de 12m), considerando-se a grelha com protensão apenas nessa viga, são apresentados na figura a seguir:
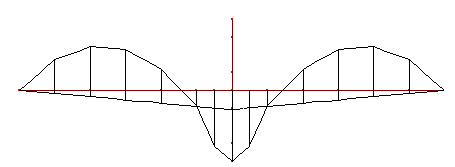
Fig. 10 – diagramas de momentos dos métodos FD e SP/TQS
Na tabela a seguir, coloca-se lado a lado os valores do momento isostático de protensão e os valores obtidos pela diferença entre os momentos do método das forças de desviação (FD) e os do método SP/TQS na primeira metade do vão da viga. Observa-se uma boa "aproximação" entre os mesmos.
| Coord . X (m) | Mo (tf.m) | FD - SP/TQS (tf.m) |
| 0,0 | 0,00 | 0,00 |
| 1,0 | -3,96 | -3,98 |
| 2,0 | -5,90 | -5,95 |
| 3,0 | -5,90 | -5,95 |
| 4,0 | -3,96 | -4,02 |
| 5,0 | 0,00 | 0,00 |
| 6,0 | 6,16 | 6,11 |
Finalmente, a tabela abaixo apresenta os deslocamentos transversais da viga maior, decorrentes novamente apenas da protensão da viga maior, calculados através dos 2 métodos. Pode-se notar a boa "aproximação" entre os mesmos.
| Coord . X (m) | M.D. (cm) | SP/TQS (cm) |
| 0,0 | 0,00 | 0,00 |
| 1,0 | 0,31 | 0,31 |
| 2,0 | 0,50 | 0,51 |
| 3,0 | 0,52 | 0,53 |
| 4,0 | 0,38 | 0,38 |
| 5,0 | 0,16 | 0,16 |
| 6,0 | 0,04 | 0,04 |
Cabe ressaltar, que a proximidade nas respostas dos dois métodos também é observada quando se trata a grelha com protensão apenas na viga menor. E, consequentemente, pelo princípio da superposição, o mesmo ocorre quando os dois cabos de protensão atuam simultaneamente.
Exemplo de Laje
O presente trabalho pretende exemplificar o cálculo da hiperestaticidade de uma laje cogumelo protendida, onde os esforços de protensão serão tratados como forças de desviação. Este exemplo foi baseado na apostila "Projeto e Cálculo de Lajes Planas Protendidas", págs. 26, de autoria do Eng. . Evandro Porto Duarte.
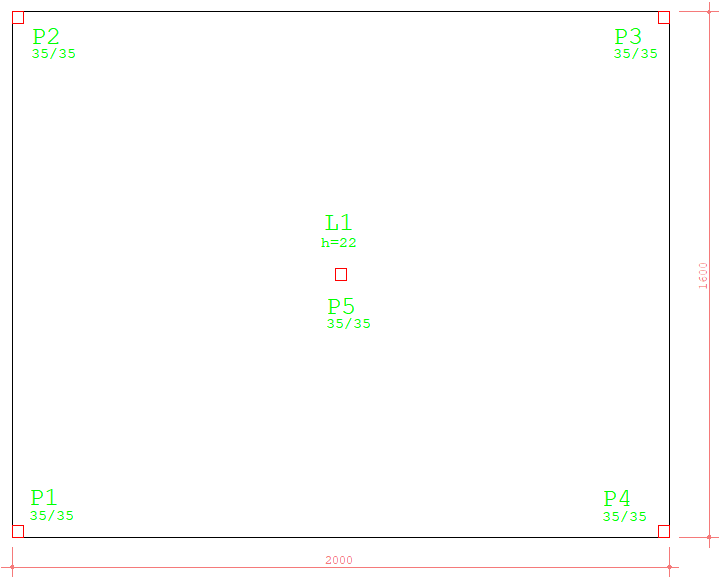
Fig 1. forma da laje cogumelo
Cargas sobre a lajes:
- permanente = 100 kg/m2
- acidental = 300kg/m2
Vamos discretizar esta laje em grelha com barras espaçadas em e com os apoios livres à rotação:
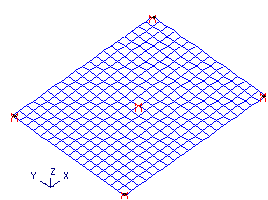
Fig 2. laje discretizada em grelha
Iremos definir na laje, as Regiões de Protensão Uniforme (RPU) nos sentidos X e Y, conforme convenção adotada na figura 2:
- Direção X:
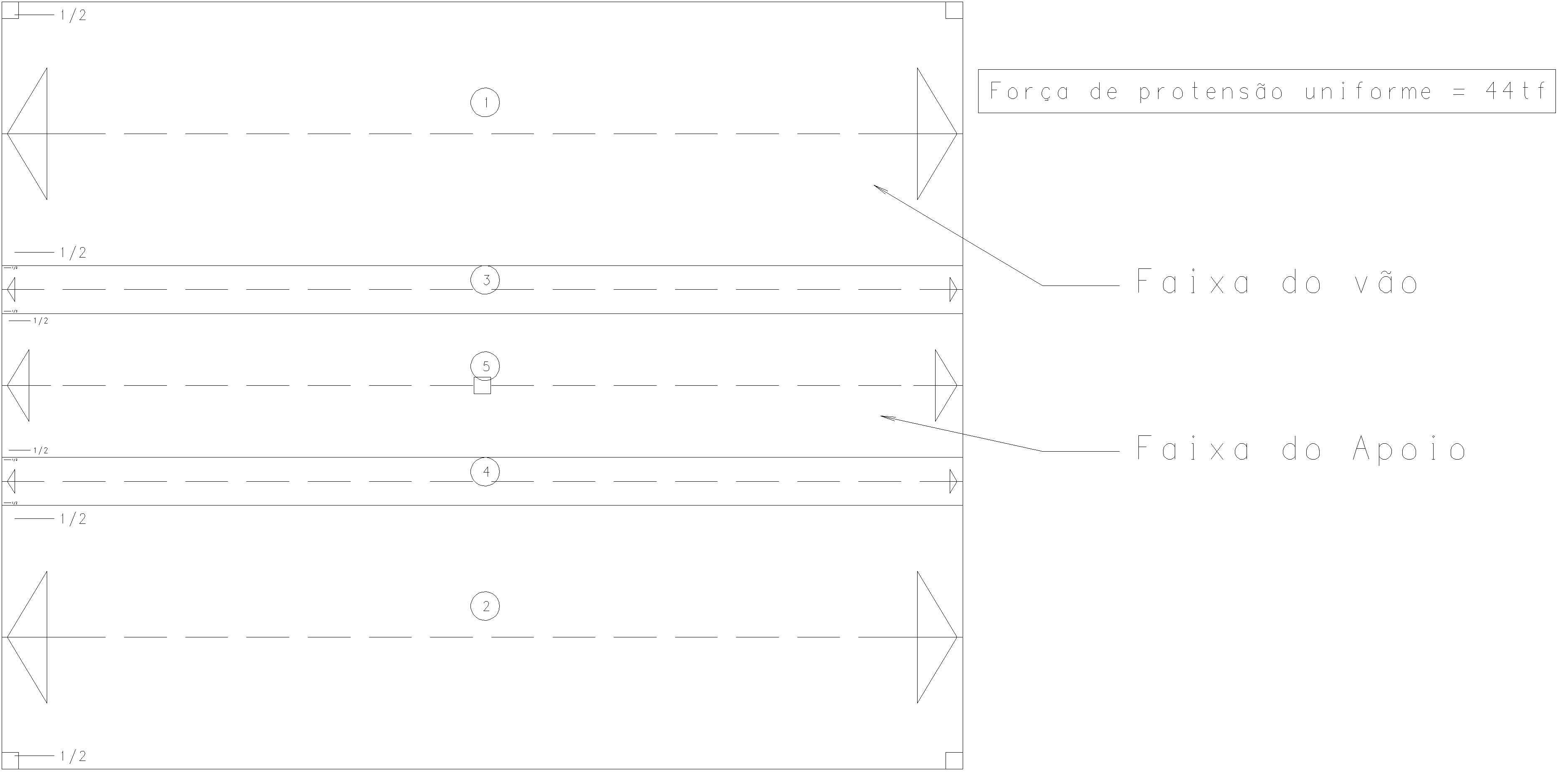
Fig 3. RPUs na direção X
- Direção Y:
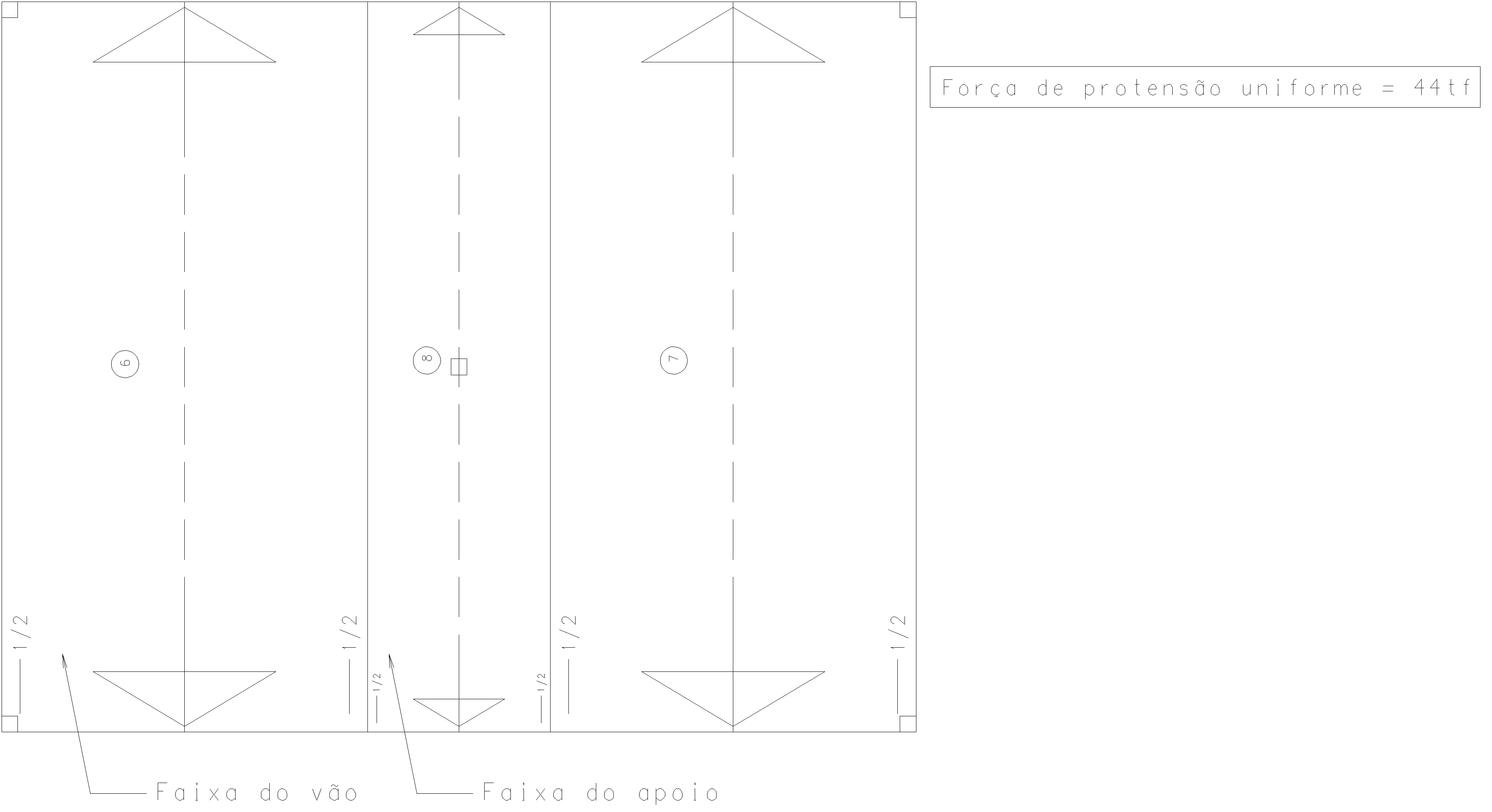
Fig 4. RPUs na direção Y
- Perfis dos cabos de protensão nas RPUs nas duas direções:
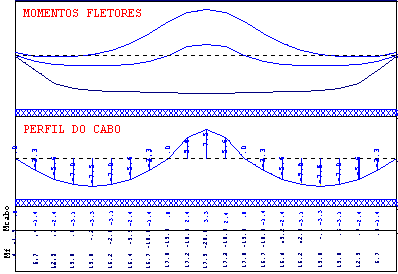
Fig 5. Perfil dos cabos de protensão na direção X - Faixa do apoio
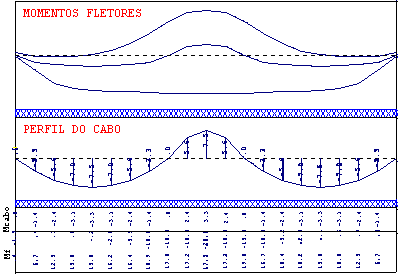
Fig 6. Perfil dos cabos de protensão na direção X - Faixa do vão
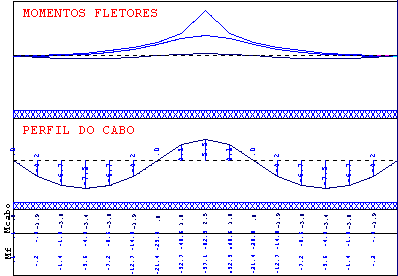
Fig 7. Perfil dos cabos de protensão na direção Y - Faixa do apoio
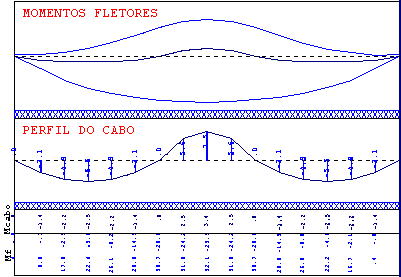
Fig 8. Perfil dos cabos de protensão na direção Y - Faixa do vão
Obtivemos os seguintes resultados devido às forças de desviação (protensão):
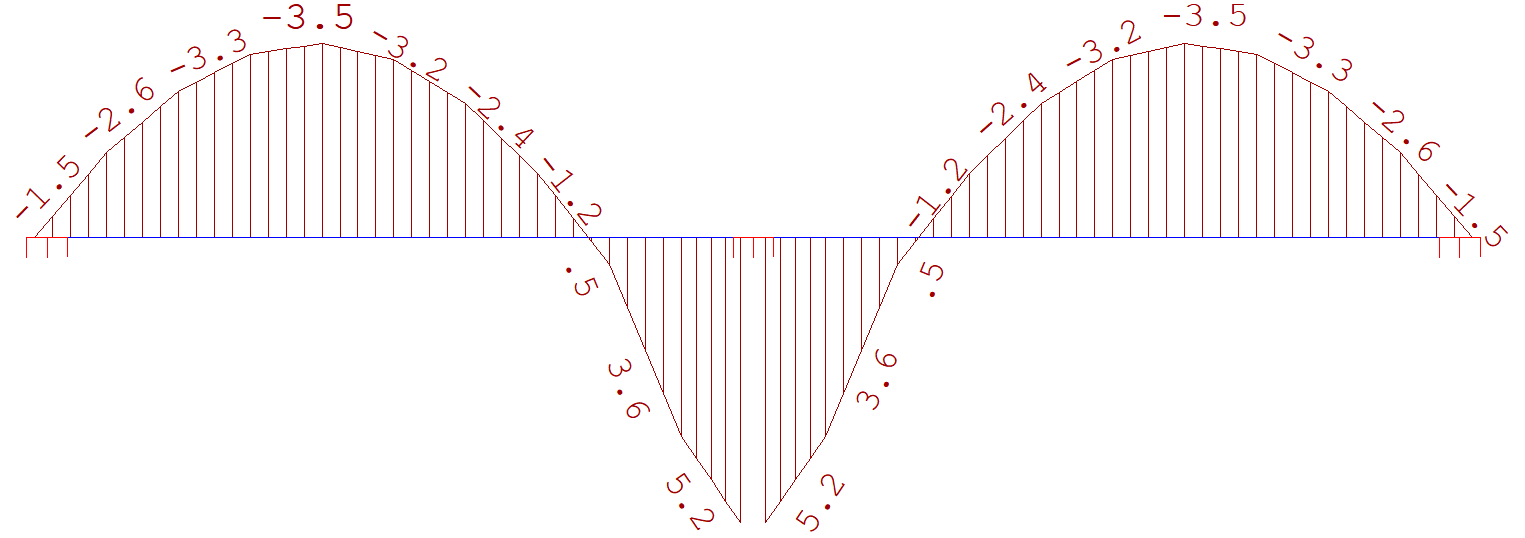
Fig 9. Momento na direção X - Faixa do apoio
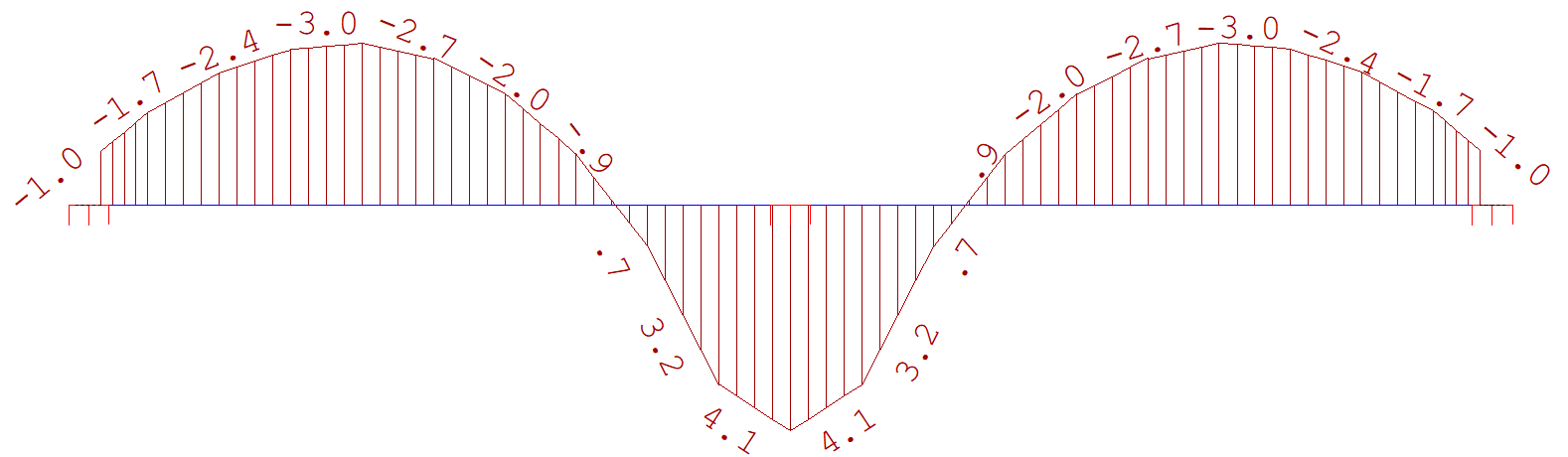
Fig 10. Momento na direção X - Faixa do vão
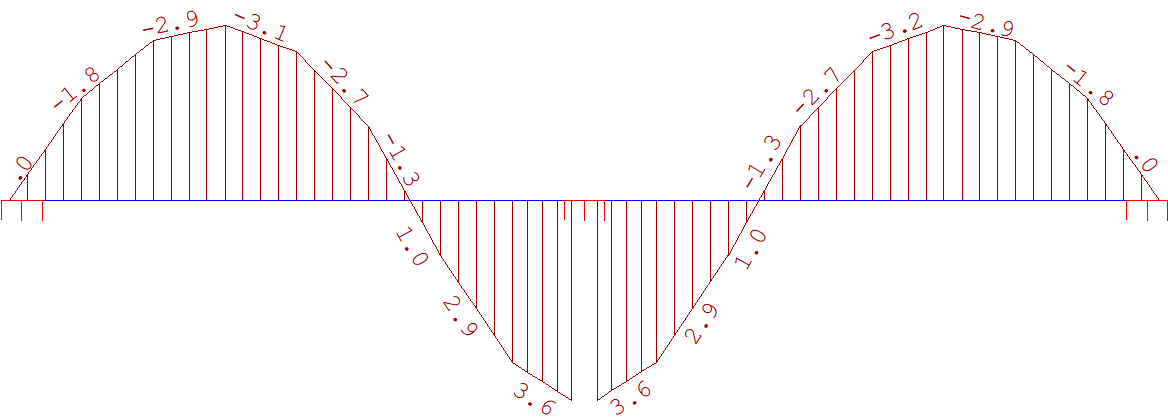
Fig 11. Momento na direção Y - Faixa do apoio
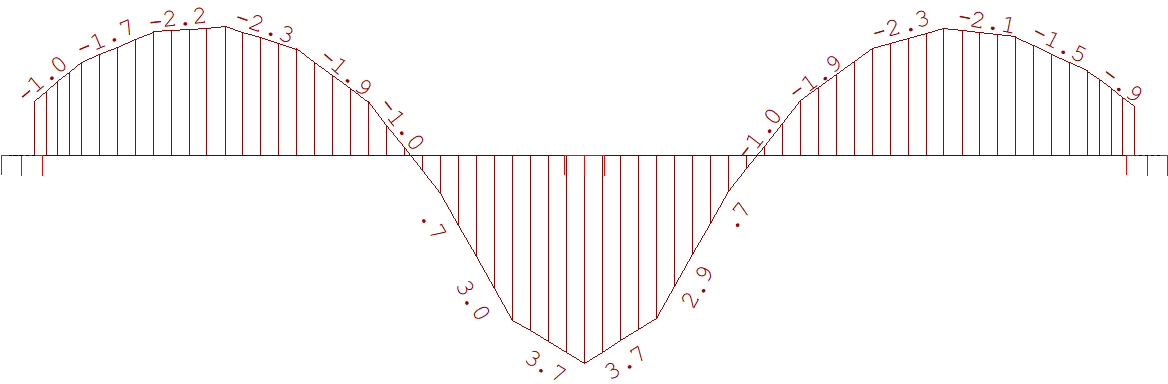
Fig 12. Momento na direção Y - Faixa do vão
Momentos devido ao hiperestático de protensão:
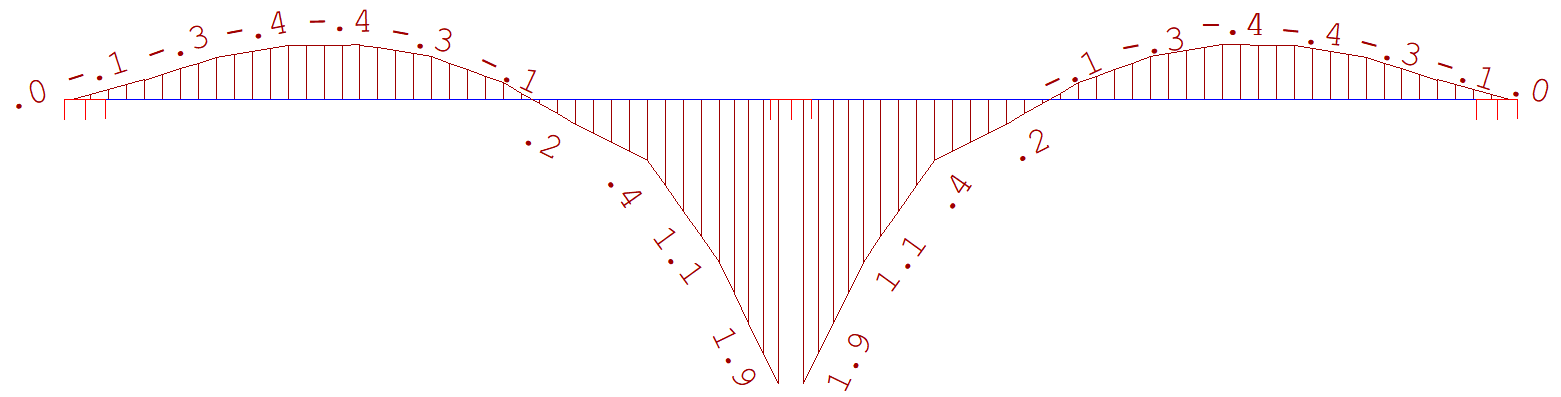
Fig 13. Momento na direção X - Faixa do apoio

Fig 14. Momento na direção X - Faixa do vão

Fig 15. Momento na direção Y - Faixa do apoio

Fig 16. Momento na direção Y - Faixa do vão
Momentos devido à ação do peso próprio + carga permanente:

Fig 17. Momento na direção X - Faixa do apoio

Fig 18. Momento na direção X - Faixa do vão
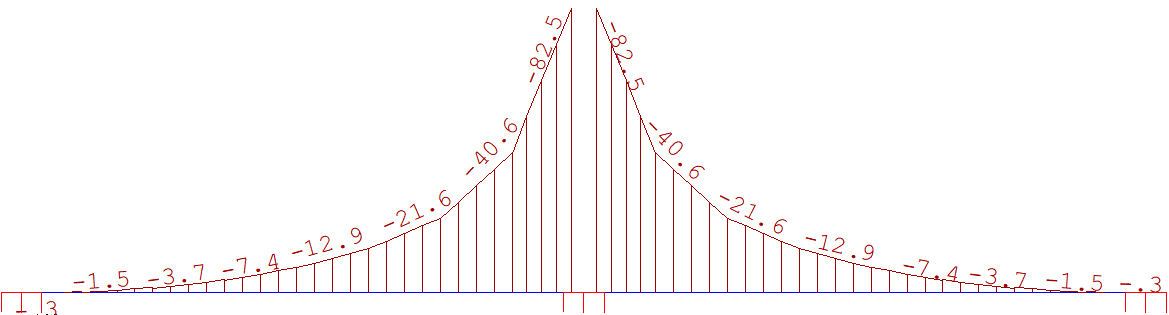
Fig 19. Momento na direção Y - Faixa do apoio

Fig 20. Momento na direção Y - Faixa do vão
Deslocamento das barras da grelha devido à ação da hiperestaticidade:
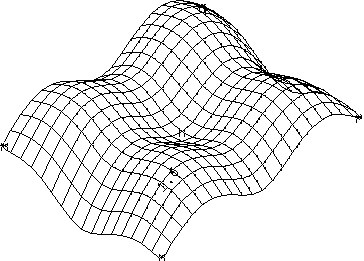
Fig 21. Deslocamento das barras da grelha
