Coeficiente de mola - Uma estaca
Mensagem extraída da Comunidade TQS
Prezado _______ e Colegas
Pela mensagem que você escreveu e tantas outras que já recebeu, quase que com certeza, você deve estar confuso na elaboração dos seus projetos. Você disse que “até começar a utilizar o TQS, não sabia da necessidade da utilização de coeficientes de molas nas fundações”.
Vamos tentar entender qual é realmente o problema.
Em primeiro lugar, é importante ressaltar que qualquer software que se utilize, este é apenas uma ferramenta de trabalho que o engenheiro dispõe. Daí a primeira duvida sua: se na escola eu não aprendi assim, como é que na utilização de um software eu tenho que aplicar as molas no meu modelo? Garanto que a sua escola deu todos os ensinamentos corretos a você, talvez pela exigüidade de tempo no curso nem todos
os casos particulares de projeto tenham sido abordados.
Uma das prioridades na elaboração de um projeto estrutural é a obtenção dos esforços solicitantes, isto é, quais os momentos fletores, forças cortantes e forças normais estão atuando na estrutura. Se soubermos onde estão as regiões tracionadas na nossa estrutura, basta quantificá-las, dimensioná-las e efetuar o detalhamento das armaduras. A dúvida principal então é: quais são os esforços? Embora esta tarefa seja, a primeira vista, simples, em determinados casos esta obtenção não é tão trivial.
Normalmente, o projeto estrutural e o projeto das fundações são elaborados separadamente. O eng. estrutural calcula as cargas nas fundações, com os apoios engastados, e o eng. de fundações dimensiona-as isoladamente. Este é procedimento que funciona na maioria dos casos mas precisa ser melhorado.
Você disse que projeta edifícios de pequeno porte, geralmente é necessário apenas uma ou duas estacas na fundação. Vamos então analisar alguns casos deste tipo no modelo estrutural global com o enfoque nos sistemas TQS.
Caso 1
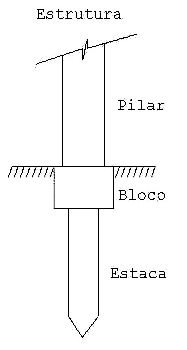
Como a estaca ainda não participa do modelo, o tipo de apoio padrão do sistema é o engastamento perfeito. O modelo estrutural ficou assim:
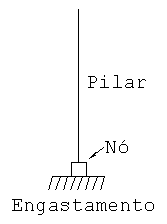
Desta forma o diagrama de momento fletor no pilar, obtidos do processamento do pórtico espacial terá a condição de engastamento no apoio. Evidentemente que a reação da estrutura no apoio terá três componentes: carga vertical, carga horizontal e
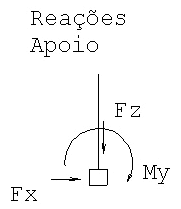
Por ocasião do dimensionamento do bloco de fundação sobre uma estaca submetido a estes três componentes ocorrerá um problema: por hipótese básica, estaca convencional única não tem capacidade para absorver momento fletor e, portanto, o bloco fica impossível de dimensionar. Por esta razão, no sistema TQS aparece uma mensagem de erro. Note que esta mensagem que apareceu no sistema TQS
ajuda ao usuário sobre eventuais problemas no dimensionamento.
Soluções possíveis para você resolver este caso:
a) Articular o apoio. Desta forma o momento fletor no apoio vai desaparecer. As reações de apoio serão apenas a força normal e a força horizontal. É uma solução não muito aconselhável para as estacas cravadas e de pouca capacidade, pois existirão excentricidades construtivas e a estaca deverá resistir a um pequeno momento fletor e, também, como a força horizontal vai ser absorvida pela fundação? Mais um ponto importante: a articulação foi feita no modelo e na realidade prática, como fica? Algum momento vai ser transmitido a estaca que não tem capacidade para tal. Esta solução não é aconselhável.
b) Projetar também a estaca para resistir às solicitações do pórtico espacial. Se você também dimensionar a fundação (e incluir o projeto de fundações juntamente com o seu estrutural), detalhar as armaduras da estaca e garantir que ela vá resistir aos esforços de momentos fletores e de forças verticais e horizontais, o projeto vai ficar perfeitamente adequado. Mas você tem que detalhar toda a estaca, geralmente as estacas de pequeno diâmetro e as pré-moldadas não atendem a este requisito. Normalmente, esta solução é boa para obras maiores, para obras de pequeno porte esta solução não é econômica. Fica apenas um problema a ser resolvido: a estaca não pode ter um deslocamento horizontal razoável e/ou uma rotação significativa pois, senão, os esforços do pórtico espacial sofrerão alterações indesejadas. Note então que o problema não é de solução trivial. Quando a estaca é projetada para um solo de baixa resistência, o efeito na superestrutura devido ao funcionamento do conjunto pilar/estaca é importante e não pode ser desprezado.
c) Colocar coeficientes de mola no seu apoio da estrutura simulando a estaca e o terreno. Não é uma solução perfeita, mas se aproxima mais da realidade. Se você calcular um vínculo elástico que simule o deslocamento horizontal da estaca e um vínculo elástico que simule a rotação da estaca, basta introduzir estes valores no pórtico espacial do TQS que você já obterá as solicitações simulando a estaca no modelo. Vou já adiantando que este cálculo de coeficiente de mola não é muito trivial, especialmente para a translação horizontal. Também neste caso, a estaca deverá ser dimensionada e detalhada para os esforços resultantes do processamento. Com os vínculos elásticos adequados, em geral, os momentos fletores que aparecem nas reações de apoios são pequenos e podem ser desprezados no cálculo do bloco. Novamente neste caso, a solução é boa para estacas sem grandes deslocamentos e/ou rotações para não inviabilizar os resultados do pórtico. Ainda assim, ficamos com o problema do cálculo dos coeficientes de molas.
d) Alterar o bloco para duas estacas em linha
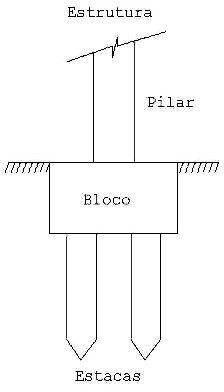 Estrutura Real Estrutura Real | 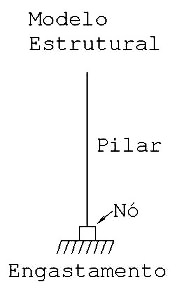 Modelo Estrutural Modelo Estrutural |
Com o bloco de duas estacas, o momento fletor vai ser absorvido por um binário de tração/compressão nas estacas. A força horizontal da reação de apoio tem que ser estudada se for significativa. Para equacionar o equilíbrio da força horizontal, basta aplicar um coeficiente de mola simulando o solo ou liberar a translação do apoio. O ideal seria calcular o coeficiente de mola adequado mas isto traz algumas dificuldades. Em geral, se o terreno for bom, e não um terreno de baixíssima capacidade, basta aplicar um coeficiente de mola de 100 tf/m que o problema fica resolvido. Note aqui que, mais uma vez, o coeficiente de mola aparece para equalizar o comportamento das estacas e da estrutura embora sem muito efeito nas solicitações.
e) Introduzir uma viga travando o bloco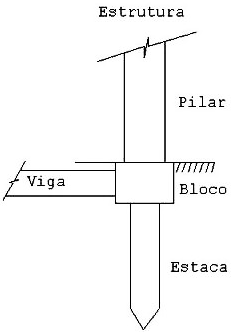 Estrutura Real Estrutura Real | 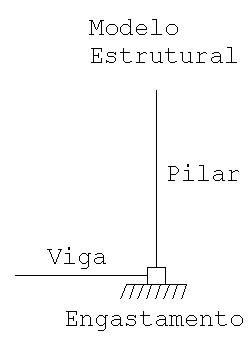 Modelo Estrutural Modelo Estrutural |
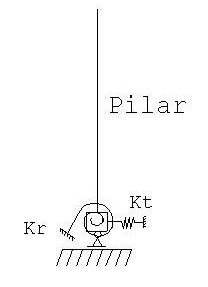
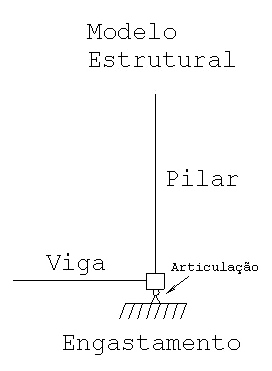
Neste caso, o momento fletor na base do pilar vai se equilibar, em parte, com o momento fletor no extremo da viga. Mesmo assim, pode aparecer algum momento fletor significativo como reação de apoio. Este momento, embora reduzido, não vai ser absorvido pela estaca e voltamos aos casos anteriores. Neste caso, ou se articula a base da estrutura ( atenção: não é articulação do pé do pilar, ver figura abaixo) ou se introduz um coeficiente de mola a rotação baixo (da ordem de 30 tfm/rad). Esta viga, geralmente, resolve o problema das forças horizontais pois ela também vai trabalhar a tração/compressão.
f) Conclusões
Este problema, aparentemente trivial, não é de solução fácil se desejarmos uma solução com maior precisão. Geralmente, para edificações de pequeno porte com vãos não muito grandes, as soluções mais indicadas são as apontadas nos itens (d) e (e), selecionando a que for mais econômica. Cuidado: todos os conceitos aplicados aqui valem para as rotações nas duas direções.
Convém recordar que o ideal seria que os momentos fletores e as forças horizontais fossem absorvidos, caso de cargas verticais, apenas pela superestrutura. Assim, a fundação iria trabalhar apenas com cargas verticais.
O suporte técnico da TQS, quando consultado sobre este assunto e sem conhecer o problema real do cliente recomenda a utilização de molas (vínculos elásticos) para resolver o problema, esta é a melhor solução técnica, a mais adequada.
Ainda na sexta-feira passada eu estive num renomado escritório de projetos de fundações. Lá tive a oportunidade de tomar contato com diversas plantas de cargas nas fundações enviadas por projetistas estruturais. A maioria delas trazia, para o carregamento de carga vertical isolado, apenas a força na direção Z (vertical), omitindo os momentos fletores e as reações horizontais correspondentes. Note então como o problema desta interface entre a estrutura e a fundação não está bem equacionado. Felizmente as demais combinações de carregamentos conforme prescrições da norma de ações e segurança estavam assinaladas.
Propositadamente, não equacionei aqui o cálculo dos coeficientes de mola para estacas (rotação e translação), pois para este porte de edificação eles não tem significado relevante.
Para tentar resolver este problema de maneira mais adequada e prática, é que estamos disponibilizando ao mercado um sistema computacional para interação soloestrutura. Mais detalhes nos jornais TQS News de números 22 e 23. Neste caso, toda a estrutura da fundação é discretizada junto com os elementos da superestrutura. O solo é considerado através dos coeficientes de mola nos elementos de fundação a partir das sondagens do terreno. Estes coeficientes de mola são, automaticamente, calculados pelo sistema. A solução final das solicitações já considera a compatibilização de toda a superestrutura e a fundação.
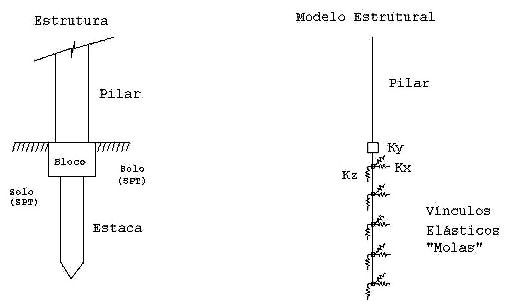
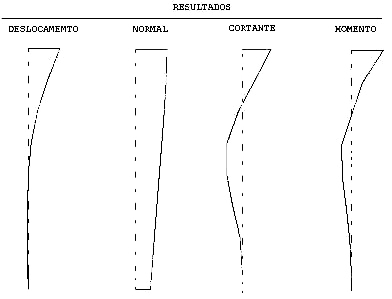
Apenas para exemplificar, vou apresentar os conceitos do SISEs para o caso de um pilar apoiando-se em uma estaca que tem a capacidade de absorver momentos fletores (apenas o cálculo de solicitações). Dados de entrada: superestrutura, tipo da estaca e suas dimensões e SPT do terreno para cada camada.
Saudações
Nelson Covas, São Paulo - SP
