Flechas - Análise não-linear versus Análise aproximada

Dúvida enviada à Comunidade TQS

O que significa a opção "Análise de flechas com resultados do cálculo com a rigidez final", presente no Visualizador de Grelha Não-Linear?

Resposta

Entendemos que as questões que foram levantadas sobre o cálculo de flechas, assim como as respectivas observações, são pertinentes e muito bem vindas. Procurar entender o que está por trás da ferramenta computacional, antes de usar a nova opção, é louvável.Inicialmente, vou procurar responder o seguinte questionamento: “se dispomos uma análise não-linear incremental e sofisticada (grelha não-linear), que gera resultados compatíveis com os medidos em obra (há relatos que indicam isso) como também com ensaios em laboratório (há artigos que indicam isso), por que foi criado um outro tipo de análise no sistema, mais aproximado, com a aplicação da carga total com a rigidez final fissurada?”.

OBS.: Essa nova opção foi criada na versão 15 e pode ser desativada/ativada por meio do critério de grelha não-linear apresentado abaixo.

 A princípio, essa nova opção, realmente, parece não ter lógica, uma vez que ela descarta toda a análise não-linear incremental, que tem se mostrado, conforme já relatado, compatível com as medições em obra.

Mas, vejamos...

Essa nova análise foi implantada no sistema de forma a oferecer ao Engenheiro mais uma opção de cálculo, que vem de encontro com a conta aproximada que muitos fazem manualmente, que tem meu apoio, e que consiste em majorar a flecha elástica resultante da aplicação do carregamento total em serviço por um coeficiente que relaciona as rigidezes integral (estádio I) e fissurada (estádio II). Certamente, trata-se de um cálculo mais conservador que a análise não-linear, na qual as rigidezes são corrigidas gradualmente, a cada incremento de carga.

Além disso, na ocasião do debate sobre flechas que tivemos há alguns meses atrás, submeti-me à chamada “revisitação teórica”, algo que recomendo sempre a todos. Reestudei o assunto que havia deixado para trás há anos. Absolutamente, não encontrei nenhuma inconsistência com relação à análise não-linear incremental proposta. Tudo estava e está plenamente de acordo com as teses e artigos que serviram de base para o sistema. O grelha não-linear não foi alterado em nada.

Contudo, depois de profícuos debates com alguns colegas, de ponto de vista estritamente teórico, percebi que a correlação entre o processo incremental adotado na análise não-linear e a resposta real da estrutura não é algo 100 % perfeito. De certa forma, isso era meio que evidente (existe algo 100 % preciso em Engenharia???). Mas, foi exatamente esse fato que mais me motivou a criar a nova opção. Por quê? Para salientar que não podemos, em hipótese alguma, nos basear apenas num único valor para dar um parecer final sobre o comportamento de uma estrutura, mesmo sendo o resultado advindo de uma análise não-linear teoricamente mais precisa. O problema em questão é muito mais complexo do que podemos imaginar. Envolve uma série de outros itens que simplesmente descartamos em nossos cálculos atuais. E o escoramento? E as falhas geométricas no posicionamento das armaduras? E a variação do módulo de elasticidade ao longo do tempo? E a fluência? Enfim, o fato é que estamos longe, mas muito longe, de saber representar o comportamento real da estrutura.

Portanto, a conclusão é: a análise não-linear incremental continua sendo uma ferramenta útil na prática de projetos. Deve continuar sendo adotada na estimativa de flechas, como muitos têm feito com sucesso. A nova opção, mais conservadora, pode ser adotada ou não como referência, a critério de cada Engenheiro. No meu modo de ver, quanto mais resultados tivermos em mãos, mais subsídios teremos para encarar o problema de frente e tomar a decisão de Engenharia correta. Dentro dessa ótica, também não podemos esquecer do resultado obtido na análise linear (com a devida consideração aproximada da fluência e fissuração), uma análise evidentemente mais simplificada, mas que não pode ser ignorada. Há também os resultados obtidos a partir de métodos simplificados (lajes isoladas + métodos elásticos ou de ruptura). Mas, esses praticamente deixaram de ser eficazes na medida que a tipologia das estruturas dos pavimentos mudou ao longo dos últimos anos. Antes, era comum termos uma viga debaixo de cada parede, resultando em lajes com vãos menores. Hoje, a situação é bem diferente. A estrutura ficou notadamente mais deformável e, conseqüentemente, mais suscetível a patologias em serviço.

Bem, com o exposto acima, espero ter contribuído na resposta para os questionamentos que foram levantados. Agora, peço a permissão para me alongar mais um pouco, apresentando algumas observações sobre determinados pontos à cerca do assunto.

I. Bibliografia

Além dos excelentes artigos elaborados pelo Profº José Milton de Araújo, darei mais uma sugestão. Trata-se de um livro que me foi apresentado pelo Profº Vasconcelos intitulado “Cálculo de Flechas en estructuras de hormingón armado”, de autoria do Dr. José Calavera Ruiz, Dr. Luis Garcia Dutari e Ing. Raúl Rodríguez Escribano. Além de apresentar as tradicionais formulações para cálculo de flechas, os autores fazem uma abordagem bastante prática e realista do problema que, repito, é muito complexo.

II. Nível de fissuração

Mais do que o valor da flecha final em si, acho que um resultado fundamental que a análise não-linear nos dá é o nível de fissuração do pavimento para o carregamento em serviço. No visualizador de grelha não-linear, por exemplo, é possível identificar claramente quando um determinado pavimento fissurou muito ou não, conforme mostra a figura abaixo.

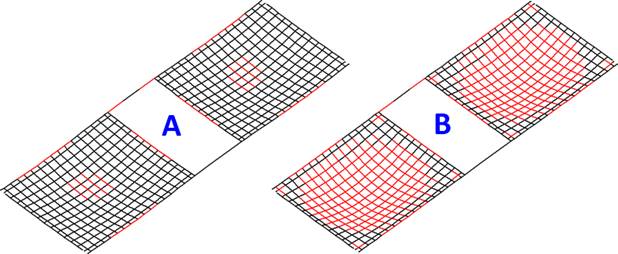
Sem entrar no mérito do valor da flecha, a situação A não é nitidamente distinta da situação B? Mesmo que a flecha esteja próxima dos limites normativos, a chance do surgimento de patologias no caso B é 100 %.

III. Critérios de grelha não-linear

Obviamente, como em todo processamento, o resultado final é totalmente dependente da configuração correta de critérios de projeto. Numa análise não-linear, essa condição é mais severa, pois o número de parâmetros é bem maior. No caso do grelha não-linear, há inúmeros parâmetros que precisam estar bem definidos. Dentre eles, destaco:

- Número total de incrementos de carga (NINC)

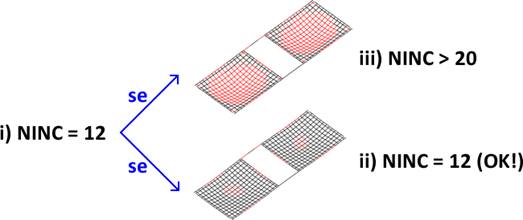
A dúvida que sempre surge é: qual o número de incrementos de carga mais adequado? Uma dica é: i) processe, inicialmente, o grelha não-linear com 10 ou 12 incrementos e entre no visualizador de grelha não-linear para verificar se o nível de fissuração está elevado; ii) se estiver, aumente o número de incrementos para no mínimo 20 e reprocesse, pois a não-linearidade provocada pelo fissuração pode ser preponderante no resultado final; iii) se não estiver, o número de incrementos inicial está de bom tamanho.

 - Parcelas de incremento para cálculo da fluência

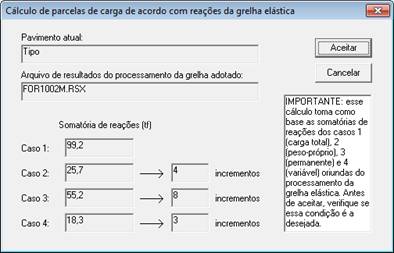
O cálculo da fluência é diretamente dependente da correta configuração das parcelas de carga (permanente imediata, permanente restante e variável). Como configurar essas parcelas? Uma dica é adotar, como referência, os resultados (reações) dos casos 1, 2, 3 e 4 da análise linear. Na versão 15, no editor de critérios de grelha não-linear, foi criado um recurso que facilita esse procedimento, conforme ilustrado a seguir.

 IV. Comentários finais

Modelar uma estrutura de concreto armado, seja para uma avaliação em ELU ou em ELS, é uma tarefa que envolve grande complexidade. A meu ver, quando se objetiva fazer uma avaliação em serviço, esse assunto se torna ainda mais crítico, pois é muito comum confrontarmos os valores teóricos obtidos em projeto (ou melhor, estimados em projeto) com os resultados reais medidos na obra em funcionamento. No ELU, esse confronto na obra é menos usual. Nesse caso, o mais comum é supormos e acreditarmos que a segurança quanto ao esgotamento da capacidade resistente dos materiais e quanto à perda de instabilidade da estrutura esteja plenamente atendida com a aplicação, em projeto, dos conhecidos ponderadores ɣf, ɣc e ɣs.

No caso do cálculo de flechas em lajes, uma verificação essencialmente em serviço, cujo objetivo é garantir conforto visual aos usuários assim como o bom funcionamento dos elementos apoiados sobre as mesmas (alvenarias), quando estamos em frente ao computador, tendemos a acreditar que os valores que estão no nosso monitor são 100 % precisos perante ao cenário real. Eu mesmo já caí nessa armadilha inúmeras vezes. O certo seria apresentarmos os resultados da seguinte forma: fobtida = 4,5 cm ± 2,0 cm, não é mesmo?

Eng. Alio E. KimuraTQS