Módulo TQS para Análise Não-Linear Geométrica de Pórticos Espaciais
Introdução
Na análise estrutural estática, nem sempre a relação forças aplicadas versus deslocamentos da estrutura pode ser considerada como linear. Tal fato pode ser decorrente das propriedades do material da estrutura e/ou da diferença existente entre as suas configurações indeformada e deformada. Deste modo, os problemas estruturais estáticos podem ser enquadrados em um das seguintes categorias:
- I. Fisicamente e geometricamente lineares;
- II. Fisicamente não-lineares e geometricamente lineares;
- III. Fisicamente lineares e geometricamente não-lineares;
- IV. Fisicamente e geometricamente não-lineares.
A maior parte dos problemas estruturais encontrados na Engenharia Civil é tratada como pertencente à primeira categoria acima. No entanto, em alguns casos práticos, como os dos edifícios altos e esbeltos sujeitos a cargas laterais devidas ao vento, os efeitos decorrentes da não-linearidade geométrica são importantes e deveriam ser considerados.
Para tratar esses casos, a TQS implementou no seu sistema um módulo para análise elástica não linear geométrica (NLG) de pórticos espaciais constituídos de barras prismáticas (eixo reto e seção constante) de material elástico linear.
O objetivo deste artigo é apresentar os principais aspectos do módulo NLG MIX-TQS, situando-o dentro do panorama geral da análise não-linear geométrica. Nas seções seguintes, será apresentado um breve resumo da teoria que fundamenta a implementação do novo módulo e que define seu domínio de aplicação. Para um maior aprofundamento nessa teoria, sugere-se, por exemplo, a leitura da bibliografia listada no final desse artigo. Serão também apresentados alguns exemplos que ilustram a importância do uso módulo em algumas casos do dia a dia da engenharia estrutural.
O problema da flexão de barras prismáticas elásticas lineares - hipótese Navier-Bernoulli
A hipótese cinemática usada no módulo NLG de pórticos espaciais para a análise do problema estrutural da flexão composta de barras prismáticas é a de Navier-Bernoulli. Em tal hipótese, admite-se que seções planas normais ao eixo da barra antes da deformação permanecem planas e normais ao eixo após a deformação. Através da adoção dessa hipótese, os deslocamentos da barra podem ser descritos a partir apenas dos deslocamentos do seu eixo.
A outra hipótese adotada no módulo, a de que o material da barra é elástico linear, implica trabalhar dentro do domínio das pequenas deformações (deformações específicas e distorções pequenas em relação a unidade). Na verdade, tal fato é que torna possível a adoção da hipótese de Navier-Bernoulli, mesmo no caso de flexão com grandes rotações como, por exemplo, a flexão com forte curvatura de uma haste de aço extremamente delgada.
No caso mais geral de flexão, o eixo da barra pode estar submetido a grandes rotações que provocam efeitos não-lineares na resposta estrutural. Conseqüentemente, o caso geral de flexão de barras com material elástico linear enquadra-se na categoria III acima descrita. Alguns autores denominam essa teoria como de 3a ordem [1].
Dependendo da ordem de grandeza das rotações, pode-se definir 2 casos particulares de flexão: a flexão com rotações moderadas (rotação da ordem de grandeza da raiz quadrada da deformação específica) e a flexão com pequenas rotações (ordem de grandeza da deformação). Obviamente, tais situações são casos particulares da flexão geral, podendo-se deduzi-las a partir da formulação geral através de simplificações compatíveis com a menor ordem de grandeza assumida para as rotações.
A restrição de que a barra está submetida a rotações moderadas não elimina a não-linearidade na resposta estrutural. Assim, esse caso de flexão de barras com material elástico linear também se enquadra na categoria III. Essa teoria também é conhecida como de 2a ordem.
No caso de flexão de barras de material elástico linear com pequenas rotações, as configurações indeformada e deformada da barra podem ser confundidas e a resposta da estrutura é linear, enquadrando-se na categoria I dos problemas estruturais. Essa teoria também é conhecida como de 1a ordem.
O tratamento do caso geral da flexão (grandes rotações) em pórticos espaciais é muito complexo. Tal complexidade deve-se principalmente ao fato de que rotações finitas no espaço 3D não podem ser tratadas como vetores. Existem 2 abordagens para esse problema. Na primeira, é necessária a redefinição dos conceitos de momento e rotação [2]. Já na segunda, aplica-se o carregamento na estrutura em pequenos incrementos, atualizando-se em seguida as coordenadas da estrutura. Os incrementos devem ser de tal forma que as rotações ocorridas entre duas configurações sucessivas sejam pequenas e possam ser tratadas como vetores [3].
No módulo NLG MIX-TQS a teoria implementada foi a das rotações moderadas. Nessa teoria, a ordem de grandeza das rotações ainda é pequena comparada à unidade, tornando-se possível tratá-las vetorialmente e considerar as flexões nos dois planos principais da seção da barra como desacopladas. Deste modo, as flexões nos planos principais xy e xz são tratadas independentemente, e seus efeitos superpostos e complementados pelo da torção.
Formulação das Equações de Equilíbrio dos Problemas NL Geométrico com Materiais Elásticos Lineares
A seguir é apresentado um resumo do procedimento descrito na referência [4] para dedução das equações de equilíbrio para estruturas sujeitas a pequenas deformações e em regime elástico linear. Nessa dedução, usam-se o princípio de minimização da energia potencial total e o método dos elementos finitos como ferramenta de discretização.
Nas expressões seguintes representa o vetor que descreve o estado de deformação e , o correspondente vetor energeticamente conjugado que descreve o estado tensional. Do mesmo modo, u representa o campo de deslocamento e F o correspondente campo de força.
Considerando-se a hipótese da linearidade do material e admitindo-se que as forças aplicadas são independentes da deformação, a energia total é expressa por:
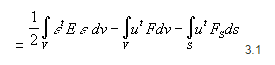
onde V e S são o volume e a superfície da estrutura na configuração indeformada, respectivamente. E Fs representa as forças de superfícies prescritas em S.
No equilíbrio estático, o funcional é estacionário, logo
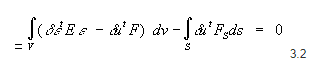
O estabelecimento da expressão 3.2 em termos dos deslocamentos nodais r requer a introdução das relações deformação-deslocamento. No método dos elementos finitos, tais relações podem ser escritas com

com
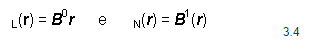
onde ![]() é função apenas das funções de forma e
é função apenas das funções de forma e ![]() é função de e r.
é função de e r.
Fazendo-se a variação do vetor deformação e executando-se algumas operações algébricas, descritas em [2], chega-se às seguintes relações não-lineares força-deslocamentos:
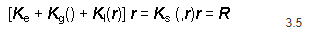
onde
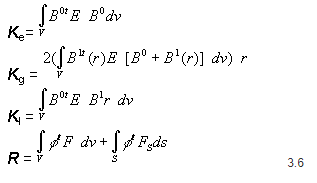
e ![]() é a matriz secante que relaciona as forças aplicadas aos deslocamentos.
é a matriz secante que relaciona as forças aplicadas aos deslocamentos.
A implementação computacional MIX-TQS para análise não linear de pórticos
As expressões 3.5 e 3.6 foram deduzidas dentro da teoria geral das estruturas com material elástico linear. As matrizes de rigidez secante utilizadas no módulo NLG MIX-TQS são determinadas particularizando-se tais expressões para o caso de uma barra de eixo reto e seção constante sujeita às condições impostas pelas hipóteses da teoria de segunda ordem de rotações moderadas, comentadas na seção 2 deste trabalho. Para o leitor interessado, as matrizes implementadas no módulo estão explicitadas na referência [5].
Através da expressão 3.5 constata-se que, nos problemas estruturais pertencentes a categoria III, a matriz de rigidez da estrutura passa a ser representada pela soma das 3 parcelas,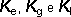 , onde
, onde ![]() é a clássica matriz de rigidez elástica linear.
é a clássica matriz de rigidez elástica linear.
No caso de estrutura formadas por barras prismáticas sujeitas a rotações moderadas ![]() é a matriz de rigidez geométrica que leva em consideração a interação entre a força axial e o momento fletor na barra.
é a matriz de rigidez geométrica que leva em consideração a interação entre a força axial e o momento fletor na barra.
Já ![]() expressa as forças axiais decorrentes dos deslocamentos nodais perpendiculares ao eixo das barra. A figura a seguir representa um caso onde esse efeito de segunda ordem é importante. Realizando-se uma análise não- linear geométrica desse exemplo, obtém-se como resultado uma força normal não nula atuando na barra. Tal força não pode ser detectada na análise linear.
expressa as forças axiais decorrentes dos deslocamentos nodais perpendiculares ao eixo das barra. A figura a seguir representa um caso onde esse efeito de segunda ordem é importante. Realizando-se uma análise não- linear geométrica desse exemplo, obtém-se como resultado uma força normal não nula atuando na barra. Tal força não pode ser detectada na análise linear.
No módulo implementado, é possível adotar-se na análise não linear:
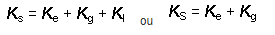
Método Empregado na solução do Sistema de Equações Não-Lineares
O sistema de equações expresso em 3.5 é não-linear. Para resolvê-lo, foi implementado no MIX o método de Newton-Raphson modificado, usando-se a matriz de rigidez elástica com matriz secante e considerando-se o vetor força em apenas um incremento.
Limitações do Módulo Não-Linear Geométrico MIX-TQS
A utilização do módulo só é possível nos casos enquadrados dentro do escopo da teoria de flexão de barras prismáticas de materiais elásticos-lineares sujeitas a rotações moderadas.
O módulo também não converge em situações de equilíbrio pós-crítico ou quando a matriz de rigidez elástica linear da estrutura for singular, por exemplo, no caso de hipostaticidade.
Existem situações onde a contribuição de Kl tende a enrijecer fortemente a estrutura. Em tais casos, embora a estrutura possa ser estável, o algoritmo de solução (solver) pode mostra-se ineficiente na determinação da resposta da estrutura.
Operação do Módulo
O módulo NLG MIX-TQS é rápido e pode ser facilmente utilizado. Com relação aos dados da análise linear, é necessário que sejam fornecidas ao programa apenas as 4 seguintes informações:
Número máximo de iterações: a análise não-linear geométrica implementada no MIX-TQS envolve um processo iterativo. É necessário que se defina o número máximo de iterações que o programa deve executar sem que se observe a convergência na análise.
Tolerância relativa: parâmetro utilizado pelo programa para verificação da convergência da análise. A convergência na análise será alcançada quando:
< tolerância relativa
onde ![]() é o vetor deslocamento da i-ésima iteração e
é o vetor deslocamento da i-ésima iteração e ![]() sua norma euclidiana.
sua norma euclidiana.
Fator para multiplicação dos resultados após a análise: fator a ser aplicado aos resultados (deslocamentos esforços e reações) obtidos na análise não-linear geométrica.
Consideração ou não da matriz ![]() na análise não linear: deve-se indica se a parcela
na análise não linear: deve-se indica se a parcela ![]() da matriz de rigidez secante deve ser ou não considerada na análise não linear geométrica.
da matriz de rigidez secante deve ser ou não considerada na análise não linear geométrica.
Todos os campos relativos às informações acima têm default que são assumidos automaticamente pelo programa se o usuário não tiver alguma objeção.
Exemplos
Com o objetivo de mostrar a aplicação do módulo e comparar os seus resultados aos do método de majoração das cargas horizontais , proposto por Vasconcelos[6], são apresentados 4 exemplos.

O primeiro exemplo é o pórtico com 16 pavimentos tipos, mostrado na figura acima, submetido simultaneamente à ação de cargas vertical e lateral. O segundo, terceiro e quarto exemplos são construídos a partir do primeiro aumentando-se o número de pavimentos tipos para 23, 30 e 40, respectivamente.
Para simplificar a análise, nesses exemplos, todos os pavimentos, inclusive o da cobertura, são iguais e as inércias dos pilares são constantes ao longo da sua altura.
A carga lateral é gerada automaticamente pelo sistema TQS e representa o vento na direção X incidindo perpendicularmente em uma das faces do edifício. Para essa direção, os valores do parâmetro de majoração gama, z, para cada um desses exemplos é igual a 1,12, 1,20, 1,30 e 1,41, respectivamente. A análise do pórtico com 40 pavimentos e gama igual a 1,41 está fora do escopo do processo de majoração z, mas é apresentada apenas para efeito de ilustração.
Na tabela abaixo, são apresentados para cada um dos casos o deslocamento lateral no topo do pórtico (ver nó indicado na figura 8.1) obtido através da análise linear (1a ordem) e da análise não-linear geométrica (NLG). Na tabela também é listado o valor do deslocamento obtido através de uma análise linear considerando-se a majoração das cargas laterais pelo parâmetro z.
| Gama z1,121,201,301,41 | desloc. linear4,811,522,034,3 | desloc. NLG5,414,129,450,2 | desloc. método z 5,319,928,648,4 |
Verifica-se, na tabela acima, que o processo de majoração produz resultados bem próximos dos da análise NLG. A concordância entre os resultados é maior para os gamas mais próximos de 1,0. Observa-se que mesmo no exemplo com z =1,41 , que é maior que o limite z =1,30 recomendado para emprego do processo, o deslocamento no topo do edifício obtido através desse processo difere menos do que 5% do obtido através da análise NLG.
Na tabela 8.2 são apresentados para cada um dos casos o momento na base de um dos pilares do pórtico (ver nó indicado na figura 8.1) obtidos através da análise linear (1a ordem), da análise não-linear geométrica (NLG) e considerando-se a majoração das cargas laterais pelo parâmetro z.
| Gama z1,121,201,301,41 | momento linear109,2174,4244,1306,6 | momento NLG120,1204,5307,7415,6 | momento método z 121,8209,3317,7432,3 |
Verifica-se na tabela acima, praticamente, o mesmo comportamento do caso do deslocamento lateral no topo dos pórticos.
Finalmente, na tabela 8.3 é apresentada para cada um dos casos a reação horizontal na base de um dos pilares do pórtico.
| Gama z1,121,201,301,41 | reação linear19,529,740,650,4 | reação NLG20,131,343,755,4 | reação método z 21,635,552,670,7 |
Observa-se, na tabela 8.3, que o processo de majoração z superestima as reações horizontais.
Deve-se salientar que, mesmo no exemplo com z =1,41, onde os valores obtidos na análise não-linear para o deslocamento horizontal no topo e o momento no apoio são cerca de 50% maiores do que os lineares, as rotações nodais não ultrapassaram em valor absoluto a 0.01 rad ou seja 0,57.
Comentários Finais
No caso da análise de edifícios altos sujeitos a cargas laterais, a flecha no topo deve ser verificada para várias combinações de carregamentos. A limitação de tais flechas no topo do edifício enrijece a estrutura de tal forma que, na prática, assegura que as suas rotações nessas análises sejam pequenas ou moderadas (relativamente a unidade).
Por exemplo, a referência [3] menciona que, nos casos práticos de edifícios altos sujeitos a cargas laterais, as rotações dificilmente ultrapassam o valor de 1,5 (0,0262 rad). Podendo-se enquadrar, portanto, a maioria de tais análises dentro do escopo da teoria das rotações moderadas. Justifica-se, deste modo, a adoção dessa teoria no módulo NLG MIX-TQS para pórticos espaciais.
Ainda na referência [3], são utilizados vários exemplos de pórticos planos e espaciais para se comparar os resultados obtidos através da análise NLG, do P- e de alguns processos de majoração das forças horizontais [6,7]. A conclusão dessa comparação é transcrita a seguir:
“De um modo geral, deve-se optar pela aplicação de modelos que permitam a análise NLG, que representam melhor o comportamento da estrutura em segunda ordem, são mais gerais e evitam as imprecisões características dos processos aproximados. Cabe lembrar que, mesmo os processos de majoração das ações horizontais, em geral mais eficientes que o processo P-, só devem ser utilizados quando os pórticos forem muito rígidos.”
Finalmente, deve-se observar que o Prof. Vasconcelos [6] alerta que o seu método não deve ser empregado na análise de estruturas com pilares que apresentem grandes variações de inércias, como, por exemplo, no caso de algumas transições e de pilares nascendo em pilar parede.
Eng. Sérgio Pinheiro Medeiros, mestre COPPE-UFRJ, doutor Poli-USP, responsável pelo Sistema MIX e colaborador da TQS Informática.
Bibliografia
[1] L.F.T Garcia, Uma Formulação Geral para Flexão Simétrica de Barras Prismáticas de Material Linearmente Elástico, RBE vol.2/n.1, 1984, pp 65-87
[2] J.H. Argyris, P.C. Dunne, D.W. Scharpf, On Large Displacement-Small Strain Analysis of Structures with Rotationl Degrees of Freedom, Comput. Meths. Appl. Mech. Engr., 14, 401-451, 1978
[3] Márcio R.S. Correa, Aperfeiçoamento de modelos usualmente empregados no projetos de sistemas estruturais de edifício, Tese de Doutorado USP São Carlos
[4] D.A. Nagy e M. König, Geometrically nonlinear finite element behaviour using buckling mode superposition, Computer methods in applied mechanics and engineering vol. 19, 1979 pp 447-484
[5] Sérgio R.P. Medeiros e Ricardo L.S. França, Um programa para análise não linear geométrica em microcomputadores, Simposio EPUSP sobre estruturas de concreto, 1989, adendo aos anais
[6] A.C. Vasconcelos, Como se pode enrijecer Edifícios muito flexíveis, La Ingenieria Estructural Sudamericana en la decada del 80; Montevideo; Anais, v.1 237-268
[7] H. Beck, G. Konig, Criteria for Judging the Stiffness of Framed Structures, IABSE Symposium, London Proceedings, 37-45
