O misterioso módulo de elasticidade
Augusto C. Vasconcelos
Salvador E. Giammusso
Resumo
Numa introdução é apresentado o histórico do aparecimento do módulo de elasticidade com Hooke e Young. Em seguida é feita uma comparação com o comportamento dos tecidos vivos. Em seguida é feita a particularização ao caso do concreto como material composto de pedra e pasta de cimento. É apresentada a variação do módulo de acôrdo com diversas normas: EC-2, DIN 1045, ACI 318-95, Revisão da NB- 1, Módulo de elasticidade dinâmico. Seguem-se alguns dados experimentais de autoria da equipe de Furnas e sua interpretação, mostrando que o módulo cresce mais lentamente do que a resistência. Segue-se um estudo detalhado do módulo em pequenas idades. Mostra-se então que o valor do módulo a ser usado nos projetos depende da finalidade, sendo possíveis variações normais de 25%. Como as fórmulas existentes só são aplicáveis para idades maiores do que 28 dias, as discrepâncias podem ser ainda maiores. É feita uma sugestão tendo em vista uma redução dos desvios: uso da maturidade ao invés da resistência como elemento de referência.
1. Introdução
Quando, em 1660, Robert Hooke [2] escreveu a lei fundamental da elasticidade sob a forma de anagrama (letras agrupadas em ordem alfabética):
Ut tensio sic vis
(tensio = extensão, deslocamento, vis = força) ele apenas afirmava que existia uma proporcionalidade entre deslocamentos e forças. Não existia, em sua época, o conceito de tensão, que somente surgiria 150 anos depois com Cauchy. Por causa da “falta de sintonia” de Hooke com Isaac Newton (1643-1727) o assunto ficou esquecido na Inglaterra por mais de 100 anos. Somente em 1802, cerca de 75 após a morte de Newton (e 100 anos depois de Hooke!) é que o físico inglês Thomas Young retomou os estudos de Hooke e avançou um pouco mais, chegando à noção de “módulo de elasticidade”. Entretanto, a conhecida falta de didática de Young tornou o assunto extremamente obscuro, a ponto de as maiores sumidades da época não conseguirem desvendar o que significava a definição:
“O módulo de elasticidade de uma substância é uma coluna (seu comprimento (l) feita dessa mesma substância, capaz de produzir uma pressão (p) em sua base, que está para o peso (?) causador de um certo encurtamento por compressão (?l), como o comprimento (l) da substância está para a diminuição (?l) desse comprimento.” ([2] pág. 4 e [3] pág. 390).
A interpretação física imediata dessa definição, com o conceito atual de tensão, é que o módulo de elasticidade corresponde à tensão que, aplicada à coluna, seria capaz de duplicar seu comprimento (no caso de tração) ou reduzir seu comprimento a zero (no caso de compressão). Young, porém, não disse isso, nem tinha condições de assim se pronunciar.
Para Young o “módulo de elasticidade era um comprimento (que provavelmente teria sido imaginado como representativo do peso da coluna feita da mesma substância e com a mesma seção transversal da coluna estudada).
O comprimento seria, na realidade, o volume para uma seção transversal de área unitária. Como era feita do mesmo material da coluna em estudo, seu peso específico multiplicado pelo comprimento e pela área unitária da seção transversal daria por resultado o peso por unidade de área causador da pressão (p) sobre a base da coluna. Portanto, o comprimento a que Young se referia era, na realidade, o produto do comprimento pelo peso específico. Esse produto é o mesmo módulo que conhecemos atualmente.
Naquela data, Cauchy ainda não havia formulado o conceito de tensão e, portanto, se Young tivesse falado em “peso”, o conceito ficaria deturpado com um módulo de elasticidade que dependeria da seção transversal. Implicitamente, Young estaria raciocinando com seções transversais unitárias, mas sua falta de didática não permitiu que ele esclarecesse esse ponto. Somente os privilegiados poderiam perceber na época o alcance de suas palavras. Tanto é assim que Love, o maior teórico da elasticidade de todos os tempos, assim se pronunciou: “A introdução de um conceito físico definido associado com o coeficiente de elasticidade, como se descesse do céu claro diretamente sobre os leitores das memórias matemáticas, marca época na história da ciência” [2].
Até hoje, os ingleses denominam o módulo de elasticidade de módulo de Young.
Tudo o que se falou sobre o módulo de elasticidade se baseava no comportamento linear dos materiais. Isso somente acontece para valores pequenos da tensões aplicadas. A realidade se mostrou muito diferente para tensões maiores do que 50 % das tensões de ruptura. Para o concreto, em particular, a falta de linearidade começa com valores muito menores de tensões. Por isso atualmente se prefere falar em “módulo de deformação” e não em “módulo de elasticidade”. O conceito de elasticidade não depende do comportamento linear, se bem que muitas vezes é assim confundido. A elasticidade pressupõe que, cessada a solicitação, a deformação desaparece em qualquer nível de carregamento. O diagrama tensão-deformação pode ser curvo (não linear) mas é descrito pela mesma curva tanto na aplicação das tensões crescentes como decrescentes. Não havendo resíduos com a supressão do carregamento, o material é denominado elástico. Se, além disso, o diagrama for retilíneo, o material é elástico linear. Somente neste caso é que se pode falar de módulo de elasticidade.
Por extensão e por comodidade, passou-se a falar de módulo de elasticidade mesmo com diagramas curvos e com diagramas diferentes no carregamento e no descarregamento.
Surgiram então os conceitos de “módulo de elasticidade secante” nos quais se substitui o diagrama real por um diagrama linear fictício da origem até o ponto de carregamento previsto e de “módulo de elasticidade tangente” no qual se substitui o diagrama real por uma reta paralela à tangente ao diagrama verdadeiro. No caso de não existir “elasticidade” fala-se de módulos de elasticidade no carregamento e de módulos de elasticidade no descarregamento. Na realidade, são expressões “forçadas” que deveriam ser substituídas para expressão mais correta “módulo de deformação”.
O estudo dos materiais dos seres vivos [4] fornece alguma luz sobre a razão de ser da não linearidade. É nos seres vivos que encontramos uma enorme diversidade de materiais com diagramas reversíveis, isto é, iguais tanto no carregamento como no descarregamento, portanto elásticos, porém não lineares. Alguns desses materiais podem ser interpretados como numeroso conjunto de fibras cada uma das quais se comportando como uma trena de aço enrolada dentro da célula. Ao ser aplicada uma tração, essas fibras se desenrolam de maneira não linear até que o desenrolamento seja total. Daí em diante as deformações se tornam muito menores pois corresponderão às deformações das próprias fibras já tornadas retas. O diagrama correspondente é uma curva bastante pronunciada terminando por um trecho reto íngreme. Ao ser suprimido o carregamento a fibra volta a se encurtar e a se enrolar, com um diagrama perfeitamente igual ao do carregamento.
Existem grandes discrepâncias em resultados de ensaios de determinação dos diagramas tensão-deformação tanto nos materiais artificiais de construção como nos materiais dos seres vivos. O motivo está nas diferentes condições dos ensaios: temperatura, velocidade de aumento das cargas, tempo de aplicação das cargas antes de cada medida, estado de umidade, material vivo ou morto, seco ou úmido.
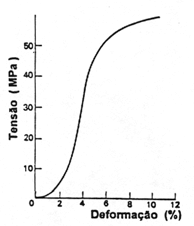
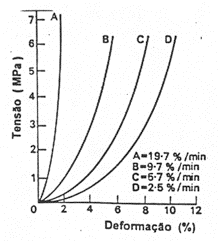
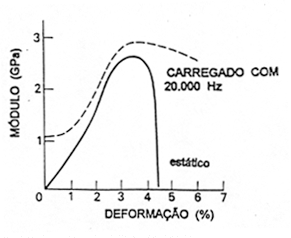
A título de exemplo é mostrado na Fig. 1 o diagrama tensão deformação do colágeno de um tendão. Até 4 % de deformação, o material é elástico não linear; cessada a solicitação, a deformação retorna pelo mesmo caminho [4]. Acima de 4 % desaparece a elasticidade (há resíduo no descarregamento) e surge ruptura com deformações entre 8 % e 10 %. O módulo de elasticidade tangente cresce gradualmente para deformações até 4 % atingindo o valor máximo de 1 000 MPa. O primeiro trecho curvo do digrama em forma de S depende bastante da velocidade de carregamento. A Fig. 2 [4] mostra essa influência em ensaios feitos por Haut e Little, em 1969, com ligamentos das pernas anteriores do cão: quanto mais rápido o carregamento, menos pronunciada a curvatura do diagrama. Para cargas aplicadas muito rapidamente, o diagrama é quase linear, o que explica o efeito favorável durante um salto. O valor do módulo de elasticidade medido em um ensaio estático é bastante diferente do módulo de elasticidade dinâmico, medido por meio de ultra-som (20 000 Hz). A Fig. 3 [4] mostra os dois módulos medidos por Mason em 1965 no tendão da cauda do
rato.
Os materiais dos seres vivos não são homogêneos. Seu comportamento varia coma a idade biológica, com intensidade e freqüência dos exercícios, com o aquecimento do organismo e com a velocidade do carregamento. Como as variáveis são mais numerosas, seu estudo ajuda a compreender o comportamento dos materiais artificiais fabricados pelo homem.
2. Aplicação ao caso do concreto
O concreto é um material não homogêneo fabricado artificialmente pelo homem. Seu caráter não homogêneo permite explicar algumas de suas propriedades que lembram certos comportamentos dos materiais vivos. A velocidade do carregamento é uma dessas influências.
Nos seres vivos, à medida que se desenvolvem as deformações, o material vai se modificando. Por exemplo, fibras enroladas vão se tornando retilíneas.
No concreto, existindo alguma solicitação, os poros cheios de ar ou água se comprimem (ou se distendem, conforme o caso) e tendem a produzir um fluxo desses fluidos. Isso demora algum tempo e, se o carregamento for lento, haverá tempo para o escoamento dos fluidos que ocupam os poros, como no caso dos seres vivos, haverá tempo para o desenrolamento das fibras (ou seu deslizamento). Se o carregamento for muito rápido, as condições em que se processam aqueles escoamentos, desenrolamentos, deslizamentos ou o que for, são diferentes e os resultados podem não ser os mesmos. Os resultados ocorrem no final do nível das cadeias moleculares, que são solicitadas diferentemente, conforme o tipo de carregamento.
Outro elemento importante é a ligação pasta-agregado. Verificou-se que, mesmo na ausência de cargas externas, existe alguma microfissuração na interface pasta-agregado Fig. 4 ([6] pág. 84).
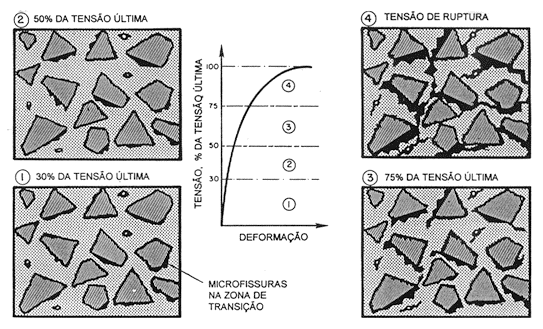
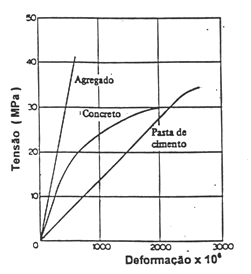
Uma maneira ilustrativa de se perceber a influência da falta de homogeneidade no comportamento do concreto em seu diagrama tensão-deformação pode ser vista no exame da Fig. 5 extraída de [5] pág. 347.
O concreto, constituído pelos mesmos materiais, apresenta um diagrama curvo desde o início do carregamento. Isto pode eventualmente explicar-se pelo fluxo de fluidos nos poros do concreto. Inicialmente é o agregado, mais rígido, que absorve quase todo o carregamento. À medida que o agregado se deforma, ele vai transferindo uma parte de seu carregamento para a pasta de cimento, que começa a se destacar do agregado. A deformação do concreto será sempre intermediária entre as deformações do agregado e da pasta. Sendo no início mais próxima da deformação do agregado, tendendo, depois, para a deformação da pasta.
Os módulos de elasticidade do concreto, que são vários em conseqüência do diagrama tensão deformação não linear, são os seguintes:
a) Módulos estáticos: determinados para uma certa velocidade de carregamento previamente estabelecida. São eles: módulo tangente na origem, módulo secante entre a origem e o ponto fixado correspondente a 40 % da resistência do concreto, módulo tangente no ponto de trabalho;
b) Módulo dinâmico: determinado com ultra-som. Equivale aproximadamente ao módulo tangente na origem.
Os maiores transtornos que ocorrem em estruturas são causados pela não consideração das deformações e dos deslocamentos corretos em idades pequenas. Desformas prematuras causam flechas excessivas em lajes. Protensões aplicadas quando a resistência é satisfatória mas os módulos de elasticidade ainda são muito pequenos acarretam contraflechas que não serão anuladas pelo carregamento futuro. Concretagens feitas em finais de tardes muito quentes e a queda de temperatura durante a noite também são fontes de distúrbios. Tudo isso mostra a necessidade de conhecer bem a relação entre o módulo e a resistência, não somente para a idade de 28 dias, mas principalmente para idades menores do concreto.
3. Variação do Módulo de Elasticidade
Deste ponto em diante, quando a expressão “módulo de elasticidade” se refere realmente ao “módulo de deformação inicial”, tangente na origem do diagrama tensão-deformação.
As diversas normas em uso nos países mais adiantados indicam expressões muito diferentes relacionando o módulo com a resistência. Para a resistência considerada aos 28 dias, distinguem-se as ora expressões que consideram resistência determinada em cubos, ora as que consideram a resistência determinada em cilindros. Recapitulam-se a seguir algumas dessas expressões, todas elas amplamente documentadas por meio de ensaios honesto, numerosos e criteriosamente executados.
Eurocódigo EC-2 [7]
O Capítulo A, referente ao concreto em [7] foi preparado pelo Prof. H. K. Hilsdorf da Universidade de Karlsruhe e fornece a seguinte expressão para o módulo de elasticidade secante para o nível de carregamento 0,4 fcm:
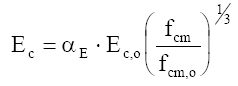
onde:
Ec = módulo de elasticidade secante para 0,4 fcm em MPa
fcm = resistência média à compressão (cilindros), MPa
fcm,o = resistência média 10 MPa aos 28 dias, referência
Ec,o = 21500 MPa módulo tangente na origem de um concreto de referência
?E = constante que depende do agregado, 1,2 para basalto e calcário denso, 1,0 para quartzito, 0,9 para calcário poroso, 0,7 para arenito;
para o caso de existirem deformações impostas irreversíveis depois da aplicação de cargas de curta duração, deve ser considerado um fator adicional igual a 0,85.
Essa expressão foi proposta pelo Código Modelo CEB-FIP MC 90 com a forma:
onde:
Ec = módulo de elasticidade secante para 0,4.fcm
fck = resistência característica do concreto
Essa expressão não corresponde exatamente a nenhum dos agregados dos indicados na expressão anterior, pois 21500/101/3 = 9979 ? 9500, o que necessitaria um fator ?E = 0,95.
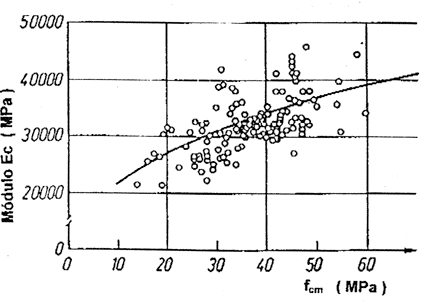
Portanto, nem mesmo o Eurocódigo estabeleceu uma expressão livre de críticas e de cálculos compatíveis. Acontece que as dispersões de valores ultrapassam a precisão que se pretenderia obter por meio de uma expressão. A Fig. 6 mostra uma comparação entre resultados experimentais e os obtidos com a aplicação dessas expressões.
DIN 1045
As expressões alemãs esclarecem que o módulo de elasticidade do concreto somente é constante para tensões pequenas aplicadas com curta duração.
O carregamento é limitado a ?p/3, sendo ?p a resistência média em cubos. Aplicando-se um carregamento com essa amplitude, com uma velocidade de 5 kg/cm²/s, obtém-se um diagrama sensivelmente linear, do qual se pode extrair um valor constante para o módulo de elasticidade Ec. Os valores que constam da norma alemã se referem exclusivamente à idade de 28 dias e são dados em função da resistência de cubos ?w do concreto, determinada em cubos com 20 cm de aresta. Aceitando uma dispersão de ± 20 %, é possível calcular Ec com a expressão:
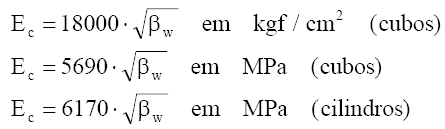
Este valor se refere ao módulo estático, havendo menção explícita de que esse é o módulo a ser usado no cálculo de concreto armado e não o módulo dinâmico, usado na avaliação do efeito de vibrações.
ACI 318 - 95
A revisão de 95 não alterou os valores anteriores de Ec. A Norma Americana é a única que fornece o valor do módulo de elasticidade em função da densidade do concreto:
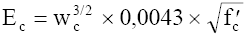
O coeficiente da raiz quadrada pode ser tomado igual a 4700 para concretos com densidades normais, qualquer que seja o tipo de agregado. Entre 1500 kg/m³ e 2500 kg/m³ ela pode ser aplicada sem grandes erros. Para 1500 kg/m³ o valor é 2500 ?fc' e para 2500 kg/m³, 5400 ?fc'. O valor médio do coeficiente seria 3950 e não 4700, o que mostra que essa expressão não deve ser aplicada com grande precisão arredondando sempre nas centenas. Para compreender a diferença entre fc’ e fck, consultar [10]. Essa fórmula foi estabelecida com grande sucesso em 1960 por Adrian Pauw e até hoje não houve contestações. Essa fórmula tende a reduzir acentuadamente o módulo dos concretos leves e a exagerar o valor para concretos muito densos.
Revisão da NBR 6118 (NB 1)
A revisão em curso da NB 1, tendo recebido numerosas críticas dos tecnologistas de concreto, afirmando que o valor de Ec calculado pela versão de 1978 é muito grande e fora da realidade brasileira, decidiu reduzir consideravelmente seu valor, tomando como base ensaios feitos na COPPE, no Rio de Janeiro e a Norma Americana ACI 318-95.
Foi proposta a expressão (valores em MPa):
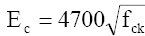
Com o coeficiente 4700 da Norma Americana substituindo o valor 4250 encontrado nos ensaios da COPPE. Julgou-se que a redução de 36 % do valor atual de 6600 para 4250 seria exagerada, aplicável somente aos agregados usuais no Rio de Janeiro. A redução menor, de 6600 para 4700 (29 %) seria mais apropriada considerando os agregados mais usuais em outros Estados.
Módulo de Elasticidade Dinâmico
Este módulo resulta de uma aplicação do carregamento, como acontece nas vibrações, sismos, choques. O concreto não tem tempo de se deformar acompanhando o carregamento. A deformação de fluência rápida, que ocorre antes do primeiro minuto de carregamento, não tem condição de ocorrer. A deformação resulta sempre menor com a velocidade estipulada de 5 kgf/cm²/s, como é prescrito pela DIN. Em conseqüência de deformações menores, é maior o módulo. Este módulo é denominado módulo dinâmico e, segundo o Código Britânico CP 110/72, pode ser relacionado com Ec pela expressão experimental seguinte (valores em MPa):
Essa expressão não é aplicável a concretos com mais do que 500 kg/m³ de cimento ou com agregados leves [5].
4. Alguns Dados Experimentais
Dispomos de informações muito valiosas contidas no trabalho recém publicado de autoria da equipe técnica de Furnas [11].
Esse livro é uma coleção de dados experimentais obtidos com diversos concretos preparados com diversos materiais. O Capítulo 6 desse livro tem o título Módulo de Elasticidade e Coeficiente de Poisson e nele se encontram respostas a muitas das perguntas que se fazem neste trabalho.
Uma análise mais detalhada, mesmo de alguns dos dados apresentados, exigiria muito espaço e, por isso, julgamos interessante algumas considerações sobre os valores apresentados no final desse capítulo, como se fosse uma conclusão dos próprios autores.
Consideramos apenas os resultados que se referem aos concretos com tamanho máximo de agregado 19 mm e 38 mm, por serem os tamanhos mais usuais na prática corrente do concreto, obtendo-se os valores que são mostrados resumidamente nas Tabelas 1 e 2.
| Resistência, fcMPa | Valor de EmínGPa | Valor de EmáxGPa |
| 20 | 23,1 | 36,9 |
| 40 | 30,7 | 45,7 |
| 60 | 33,2 | 49,7 |
| 80 | 34,4 | 50,2 |
| Resistência, fc MPa | Valor de Emín GPa | Valor de Emáx GPa |
| 10 | 16,1 | 26,0 |
| 20 | 25,3 | 36,6 |
| 30 | 31,8 | 42,4 |
| 40 | 36,4 | 46,3 |
| 50 | 39,8 | 48,9 |
| 60 | 41,0 | 49,9 |
Os valores de correlação obtidos foram os seguintes:
Sendo fc em MPa e E em GPa.
Os valores de A e B são dados nas Tabelas 3 e 4. Para verificar o efeito dos valores extremos foram suprimidos os pontos correspondentes a resistências 80 MPa, na curva a) e nas curvas b), em um caso, 60 MPa e no outro, 10 MPa e 60 MPa.
| Intervalo | Curva | A | B | r2 |
| 20 e 80 | mín | 9,91 | 0,29 | 0,948 |
| máx | 18,85 | 0,23 | 0,947 | |
| 20 a 60 | mín | 8,51 | 0,34 | 0,971 |
| máx | 16,28 | 0,28 | 0,990 |
| Intervalo | Curva | A | B | r2 |
| 10 a 60 | mín | 4,98 | 0,53 | 0,982 |
| máx | 11,70 | 0,37 | 0,972 | |
| 10 a 50 | mín | 4,52 | 0,57 | 0,993 |
| máx | 10,82 | 0,39 | 0,984 | |
| 20 a 50 | mín | 5,79 | 0,50 | 0,994 |
| máx | 12,24 | 0,32 | 0,994 |
É interessante notar que os valores mínimos se mostram aproximadamente proporcionais à potência 1/2 da resistência, ao passo que os máximos aparentemente são proporcionais à potência 1/3 da resistência. Em outras palavras, com iguais incrementos de resistência, os módulos de elasticidade de concretos com resistências maiores apresentariam incrementos menores.
Isso se ilustra derivando a expressão geral de E em função de fc e separando as varáveis:
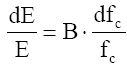
Passando para acréscimos finitos, desde que pequenos, pode-se escrever:
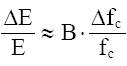
Portanto, a variação relativa do módulo de elasticidade é proporcional à variação relativa de resistência multiplicada pelo expoente B da expressão acima.
Assim, pode se esperar que, para resistências mais baixas (como pode ocorrer às primeiras idades do concreto), uma variação de, por exemplo, 10 % da resistência pode corresponder a uma variação de cerca de 5 % do valor de E, ao passo que uma igual variação, com resistências mais altas, pode corresponder a variação de cerca de 3 % do valor de E.
5. O Módulo de Elasicidade do Concreto às Primeiras Idades
Em idades bem tenras, isto é, horas, o módulo de elasticidade como que “aparece” e, em seguida, “cresce” rapidamente apresentando, em seguida um crescimento mais lento. Esse crescimento “relâmpago” já não é notado após cerca de 1 dia de idade.
Um trabalho interessante a esse respeito foi apresentado por Byfors em 1980. Desse trabalho nos chegou às mãos apenas uma página com dois gráficos que mostram o valor do módulo de elasticidade aparecendo entre cerca de 6h de idade e aumentando bruscamente até cerca de 30 GPa até entre 8h e 24h, dependendo do tipo de cimento, apresentando, depois disso, um crescimento muito pequeno.
As expressões encontradas por esse autor para a relação entre o módulo de elasticidade, em MPa, e a resistência do concreto, em MPa, são reproduzidas a seguir:

Observamos que a terceira expressão pode ser usada para valores iguais ou maiores do que 0,87 MPa, sem necessidade da expressão para valores intermediários.
Desse trabalho, pode-se concluir: como consequência do crescimento muito abrupto em relação aos valores da resistência nas primeiras idades resulta uma indeterminação muito grande do módulo de elasticidade com menos de um dia de idade e após “instalado”, o módulo de elasticidade aumenta muito pouco, o que já é um fato conhecido. Esse comportamento do concreto às primeiras idades faz supor que o módulo de elasticidade seja devido principalmente aos fenômenos localizados na interface pasta-agregado.
Neville, chama atenção para o fato de que se sabe que existe uma relação geral entre o módulo de elasticidade do concreto e a sua resistência mas não existe uma representação precisa dessa relação. Isso porque o módulo de elasticidade do concreto é influenciado tanto pelo módulo de elasticidade do agregado, como pelo teor em volume de agregado no concreto. Enquanto este último é facilmente determinado, o módulo de elasticidade do agregado poucas vezes é conhecido. Talvez seja essa a razão pela qual em certas expressões para o módulo de elasticidade como aquela do ACI 318-89 o módulo de elasticidade do agregado, comparece como um coeficiente que é função da massa específica do concreto elevada à potência 1,5 (às vezes, essa potência é tomada igual a 2). No entanto, nenhuma das expressões leva em conta a aderência entre o agregado e a pasta de cimento que o envolve. Essa aderência depende da região da interface, cuja microestrutura, segundo se sabe, é diferente da do resto da pasta de cimento hidratada e é onde se localizam as denominadas microfissuras de aderência. A microfissuração é importante para a forma da curva tensão-deformação, influenciando o comportamento do concreto e não apenas o módulo de elasticidade, que é apenas um valor ideal da relação entre tensão e deformação em determinadas condições.
Considerando-se a natureza de material composto do concreto, pode-se observar que tanto o agregado como a pasta de cimento, quando submetidos separadamente a ação de esforços axiais, apresentam curvas tensão-deformação sensivelmente lineares, apesar de terem surgido menções a não linearidade dessas relações no caso de pastas de cimento submetidas a tensões elevadas. Mas, a principal explicação para a não linearidade acentuada da curva tensão deformação do concreto está nas interfaces, nas quais se desenvolvem microfissuras mesmo sob a ação de esforços moderados. A evolução progressiva dessas microfissuras foi confirmada por radiografias de nêutrons.
A microestrutura da zona de interface é diferente da do restante da pasta de cimento devido ao “efeito de parede” que impede uma melhor disposição das partículas de cimento junto às superfícies do agregado, tanto graúdo como miúdo. Isso significa que a há menos cimento e, portanto, mais vazios, junto a essas superfícies. Em consequência, a pasta tem uma porosidade muito mais alta na região da interface do que no restante da pasta e, portanto, menor resistência.
O uso de pozolanas e de fumo de sílica, reduz o efeito de parede, devido ao tamanho menor das partículas, permitindo uma acomodação melhor junto às superfícies do agregado.
A redução do efeito de parede não só aumenta a resistência do concreto, devido ao efeito sobre a aderência pasta-agregado, mas também melhora o módulo de elasticidade, pois como a pasta tem a sua fissuração retardada, o módulo de elasticidade do agregado tem maior participação no comportamento do concreto sob ação de solicitações.
6. Qual o valor de Ec que deve ser usado?
Depois de tomar conhecimento de tanta discrepância entre os valores regulamentados pelas diversas normas, seria oportuno um comentário quanto ao valor a ser adotado nos cálculos.
Na determinação dos esforços solicitantes, o valor do módulo comparece somente quando há necessidade de avaliar as deformações impostas. Efeitos de origem térmica e de retração do concreto introduzem deformações impostas que devem ser compatibilizadas com deformações elásticas do concreto. Aí intervém o valor de Ec. Se for adotado um valor muito grande, os esforços que aparecem podem ser exagerados. Assim, por exemplo, se, em uma estrutura, sob a ação de uma acréscimo uniforme de temperatura de 20ºC, surgir uma deformação igual a ?T = ?.?T = 0,00001 × 20 = 0,02 %, surgem esforços que tendem a deformar a estrutura. Supondo-se que a estrutura seja parcialmente flexível, deformado-se sob a ação dos esforços de origem térmica e que a deformação final seja apenas a metade daquele valor, isto é, 0,01 %, para um concreto com resistência média de 25 MPa, os diversos valores calculados do módulo secante e os esforços atuantes, em consequência, sobre a estrutura, seriam os mostrados na Tabela seguinte:
Valores de tensão térmica induzida segundo diversas normas:
| Norma | Expressão de Ec | Tensão induzida |
| EC - 2 | 0,9 × 251/3 | 2,5 MPa |
| DIN 1045 | 6170 × 251/3 | 2,8 MPa |
| NBR 6118 (revisão) | 4700 × 251/2 | 2,1 MPa |
| ACI 318-95 | 4700 × 251/2 | 2,1 MPa |
As diferenças de até 25 % podem, em certos casos ultrapassar determinados limites, exigindo uma reformulação do projeto.
Como uma última evidência da indefinição, ou incerteza, da correlação entre resistência e o módulo de elasticidade do concreto, reunimos no gráfico da Figura 7 todos os pares de resultados de resistência e módulo de elasticidade a diversas idades, que constam na Tab. 6.8.a, pág. 6.54 da Ref. [11]. Nessa Figura aparecem também as envoltórias dos valores compreendidos entre 0,75 e 1,25 vezes o valor da curva de tendência os parâmetros dessa curva e o coeficiente de correlação.
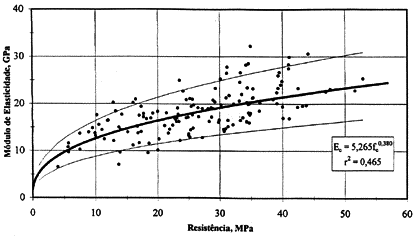
A pergunta do título ainda não foi respondida. O valor a ser usado nos cálculos depende da finalidade. No caso de avaliação de esforços devidos a deformações impostas, o valor de norma pode ser usado, não obstante a discrepância entre os diversos regulamentos. Isso significa que não tem sentido o exagero matemático com muitas casas decimais, como acontece sempre que se usa o computador. Ao se calcularem tensões no concreto em MPa, já é duvidosa a primeira casa depois da vírgula! Quando se procura avaliar o efeito, as discrepâncias são geralmente muito maiores, pois raramente a protensão é aplicada depois de 28 dias. As fórmulas apresentadas, em geral, só valem para concretos com, no mínimo, 28 dias de idade!
Como a protensão é geralmente aplicada aos 7 dias, às vezes antes, as deformações esperadas são sempre maiores. Isso se verifica freqüentemente no caso de peças pré-moldadas fabricadas em pistas de protensão. Neste caso é comum o uso de cura a vapor. A idade do concreto não é mais a idade de calendário e sim a idade fictícia determinada em função da maturidade. Entretanto, mesmo que a idade fictícia seja igual a 28 dias, as fórmulas dos diversos regulamentos não são aplicáveis, pois todas elas pressupõem uma cura normal a 20ºC. Não existe ainda uma fórmula milagrosa para contemplar os casos de cura térmica. As variabilidades são maiores ainda, pois os componentes químicos que resultam da hidratação do cimento são produzidos em ordem e em proporções diferentes conforme o diagrama de variações de temperatura durante a cura e também conforme o tipo de cimento utilizado.
Até agora não se falou no tipo de cimento. Qualquer que seja o cimento, a cura térmica altera, em geral para menos, a resistência aos 28 dias de calendário. Com esse tipo de cura, são obtidas resistências maiores às primeiras idades, porém, aos 28 dias, a resistência será sempre menor do que a obtida com cura normal. Em idade alguma seria alcançada resistência igual à obtida sem o uso de calor. Quanto mais elevada a temperatura durante a cura (não se devendo nunca ultrapassar 80ºC) e quanto mais rapidamente for aplicado o calor, maior será a redução da resistência final. O módulo depende da resistência, porém não da mesma maneira que para cura normal. Entretanto a sua determinação deve ser feita experimentalmente em cada caso.
A influência da distribuição do calor dentro do concreto é tão importante para o módulo que, em uma pista de protensão, ocorrem grandes diferenças de contraflechas em peças fabricadas em uma mesma pista, com os mesmo cabos. Isso se deve a diferenças de distribuição de temperaturas durante a cura e, provavelmente, também, em decorrência de alguma diferença de adensamento do concreto. É comum constatar contraflechas em telhas trapezoidais de 20 m variando de 7 cm a 14 cm, em peças idênticas, fabricadas simultaneamente. Isso só pode resultar de diferenças localizadas durante que tenham ocorrido durante a cura.
É curioso lembrar que as peças retiradas da pista recebem, no ato da liberação, as maiores tensões de compressão em toda sua vida útil. A resistência do concreto nesse momento deve obrigatoriamente obedecer ao valor especificado mínimo, sob pena de esmagamentos localizados ou de escorregamento dos fios, ancorados por simples aderência. A resistência pode ser satisfatória, porém o módulo de elasticidade pode estar com valor muito menor do que se poderia esperar por aplicação de fórmulas ou de experiência executiva. Esse é o grande problema que aflige todos os produtores de estruturas pré-moldadas.
Para o cálculo de deslocamentos (flechas, contraflechas, alongamentos térmicos contidos e outras) é fundamental um estudo criterioso do módulo de elasticidade, quando necessário, às primeiras idades e em condições diferentes de cura.
7. Conclusão
Depois de todas essas considerações, pode-se concluir que os fatores que determinam o valor do módulo de elasticidade do concreto são muito diversos e a influência não é muito bem definida.
Embora se saiba que o módulo de elasticidade aumenta com a resistência, sabe-se também que essa relação não é facilmente determinável, pelo menos não se consegue chegar a uma expressão genérica que represente essa relação, a não ser com uma dispersão de valores da ordem de até 25%. Essa indefinição não permite avaliar as deformações com um grau de certeza satisfatório.
A melhor forma de se conseguir uma correlação entre valores dessas duas características seria através de estudos prévios feitos com o próprio concreto com que se vai trabalhar. Isso significa, os mesmos materiais, nas mesmas proporções e nas mesmas condições.
O assunto ainda permanece em aberto...
Bibliografia:
[1] VASCONCELOS, A.C. - Da invenção do conceito de tensão aos cabos de protensão com fibras artificiais, in 36ª REIBRAC, Porto Alegre, Set. 1994 (Conferencia Inaugural do IBRACON)
[2] LOVE, A.E.H. - A treatise on the mathematical theory of elasticity, Dover Publications, New York, 1944.
[3] SZABÓ, I. - Geschichte der mechanischen Prinzipien, Birkhäuser Verlag, Basel und Stuttgart, 1977.
[4]WAINWRIGHT, S. A.-BIGGS, W. D. -CURREY, J. D. -GOSLINE, J. M. - Mechanical Design in Organisms - Princeton University Press, New Jersey 1982.
[5] NEVILLE, A. M. - Propriedades do concreto (tradução de Salvador E. Giammusso), Ed. PINI 1ª edição, São Paulo, 1981
[6] MEHTA, P. K. e MONTEIRO, P. J. M. - Concreto: estrutura, propriedades e materiais, Ed. PINI, São Paulo, 1994.
[7] HILSDORF, H. K. et al. -Concrete Structures Euro-Design Handbook, Ernst & Sohn Verlag, Berlin 1995, pág. 38.
[8] ACI 318-95 : Building Code Requirements for Structural Concrete (+Comment)
[9] LEONHARDT, F. - Vorlesungen über Massivbau - 1º vol. - Springer Verlag , 2ª ed. 1973
[10] GIAMMUSSO, S. E. e VASCONCELOS, A. C. - Qual a diferença entre a fck e a fc' do ACI? in revista ENGENHARIA no 498 , São Paulo Set/Out. 1993, pág.40-3.
[11] PACELLI DE ANDRADE, W. e equipe de Furnas, Laboratório de Concreto e Departamento de Apoio e Controle Técnico - Concretos: Massa, Estrutural, Projetado e Compactado com rolo (Ensaios e Propriedades), Vol. I, Editora PINI , 1997.
