Verificação de uma estaca (pilar) submersa de seção variável.

A seguir, apresenta-se um exemplo de verificação de uma estaca (pilar) de seção variável submersa no mar que sustenta uma parte de uma superestrutura de uma ponte por meio do pórtico não-linear físico e geométrico (NLFG) do TQS. Foram consideradas vinculações elásticas na parte inferior do elemento para simular o solo, bem como também no topo para adequar a rigidez de uma ponte. A análise possibilitou estimar a carga crítica no topo da estaca.

Inicialmente, foi criado um edifício com pisos intermediários onde serão definidas as molas do solo e a variação de seção da estaca.

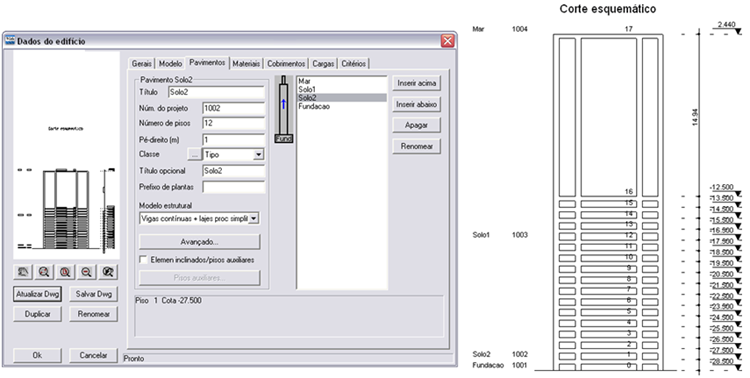
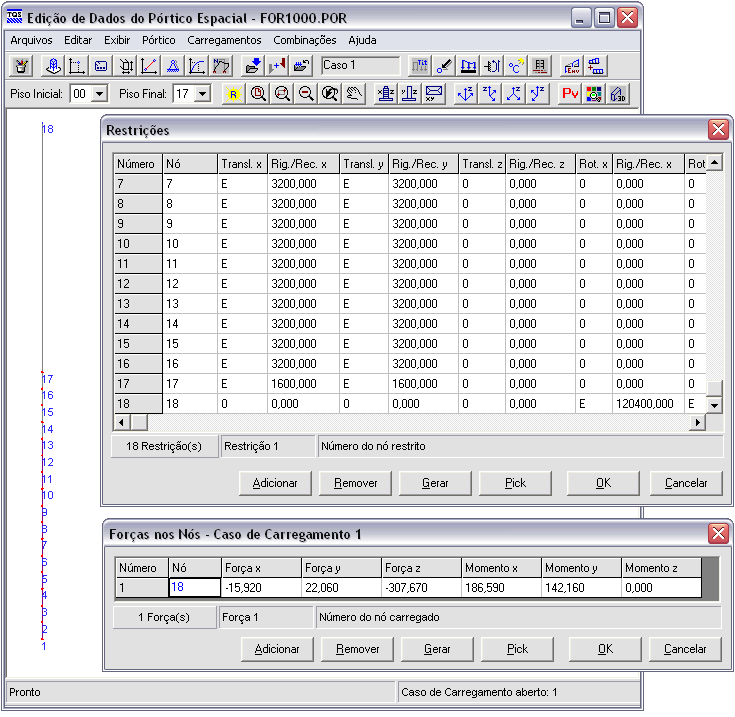
A estaca foi modelada por um único elemento com variação de seção. Foi executado o processamento global para montagem de um modelo inicial. Depois, foram impostas as condições de contorno (molas) e os carregamentos no programa de edição de dados de pórtico.

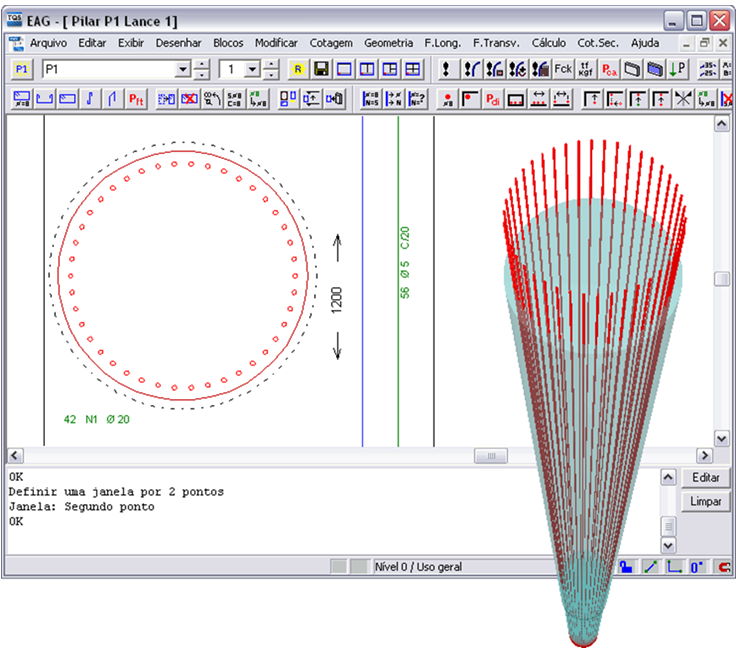
No editor de pilares, foram adicionadas as armaduras previamente conhecidas.

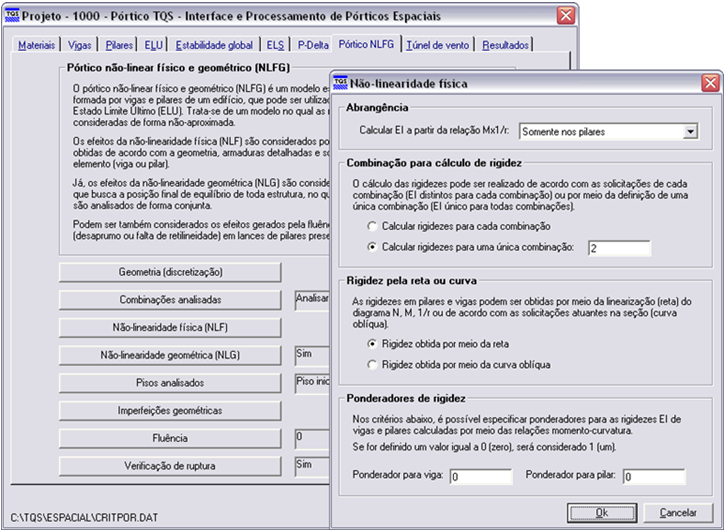
Foram configurados os critérios do pórtico não-linear físico e geométrico. O cálculo da rigidez EI foi habilitado somente para pilares (estaca). A favor da segurança, foi determinada a análise pela reta, muito embora fosse possível também utilizar a superfície N, M, 1/r (curva oblíqua) para cada seção.

A imperfeição geométrica foi simulada por uma inclinação global, resultando uma excentricidade no topo de 4,2 m em ambas as direções.

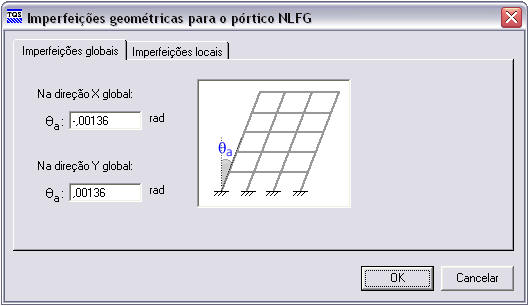
Executando o processamento do pórtico NLFG, chegou-se numa rigidez média igual a 0,24*.EIc.

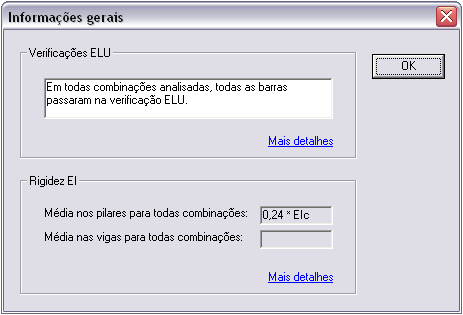
Lembrando que foi adotado um GamaC = 1,9, conforme definido nos dados da estaca.

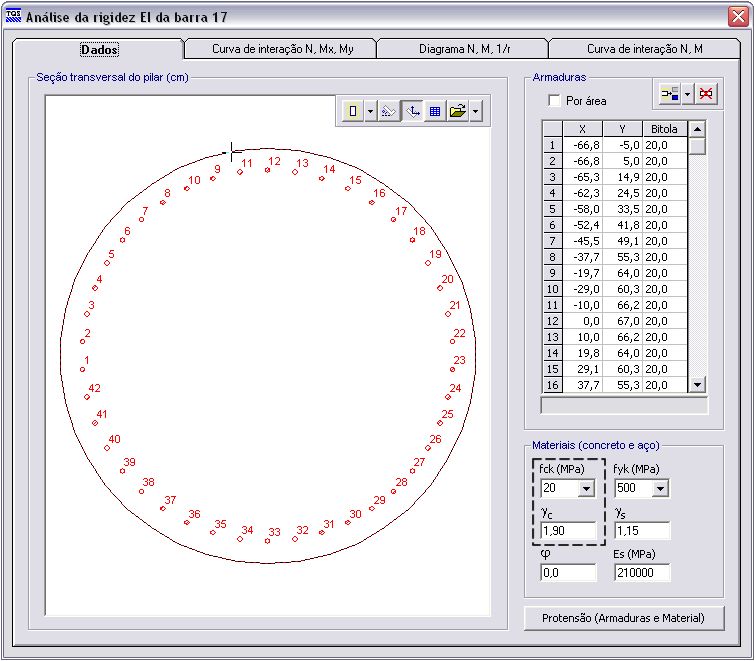
A rigidez secante obtida pelo diagrama N, M, 1/r é apresentada a seguir.

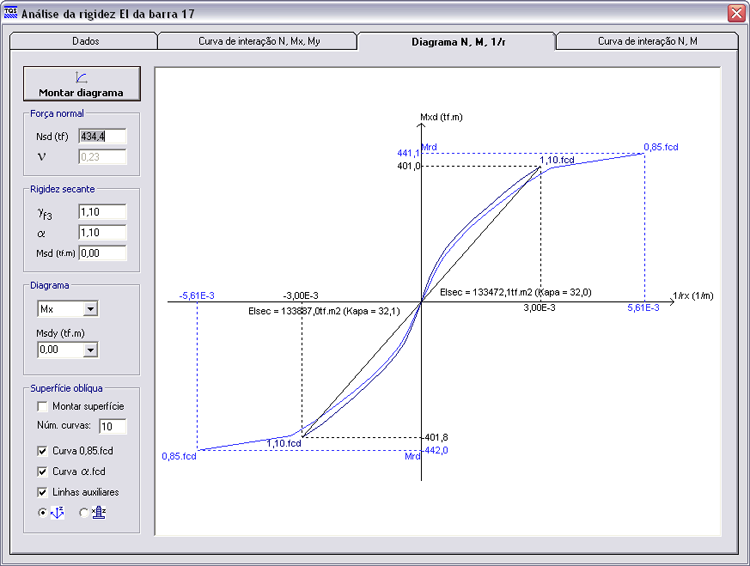
Seria possível fazer a análise também utilizando a rigidez obtida pela superfície N, M, 1/r para cada seção.

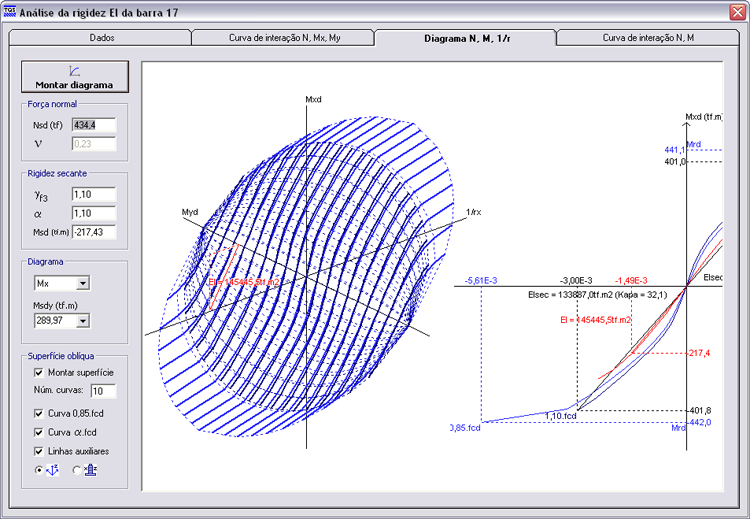
Dessa forma, rigidez média atingiria 0,58*.EIc.

No visualizador de pórtico NLFG, é possível visualizar os diagramas de deslocamentos (1ª e 2ª ordem) e força normal (NSd = 430,7 tf no topo e NSd = 539,8 tf na base).

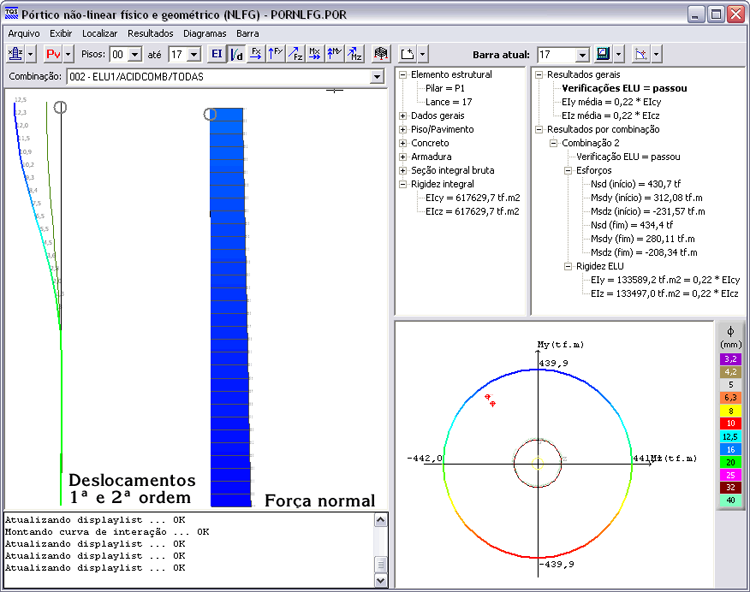
Força cortante (VSd = -23,0 no topo) e momento fletor numa direção (MSd = -231,6 tf.m no topo e MSd = 156,4 tf.m junto ao topo do solo submerso).

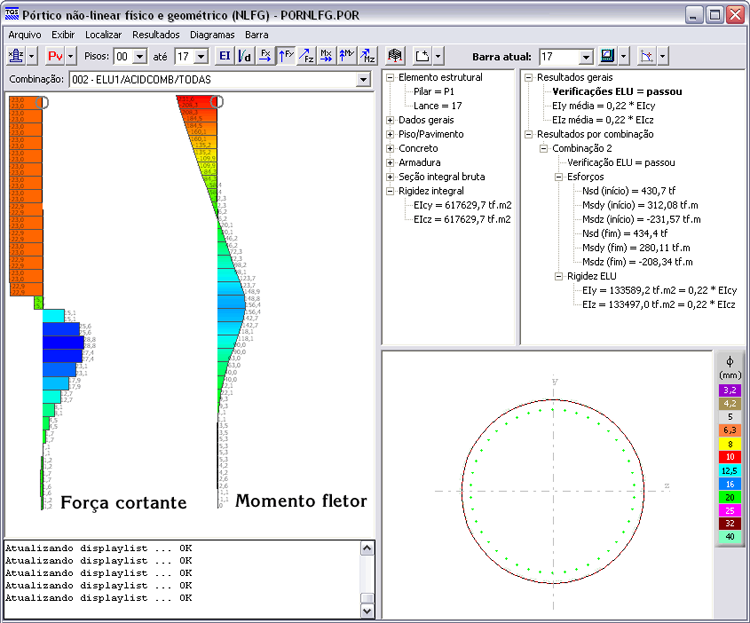
Força cortante (VSd = -31,4 no topo) e momento fletor na outra direção (MSd = 312,1 tf.m no topo e MSd = -220,8 tf.m junto ao topo do solo submerso).

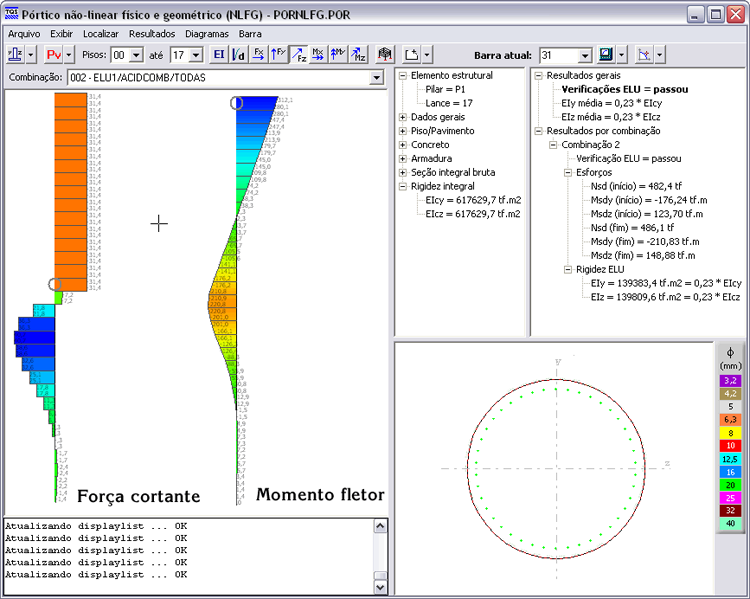
A seção crítica é a do topo, cuja curva de interação é apresentada a seguir.

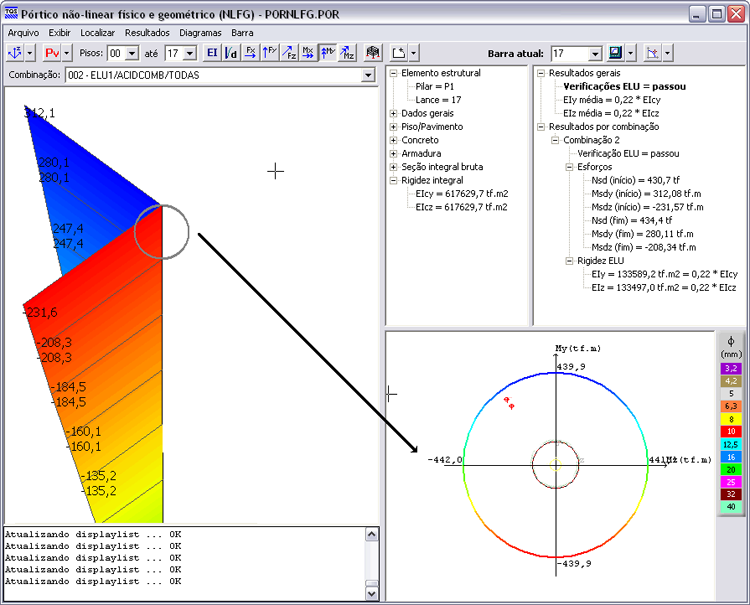
Fazendo alguns processamentos iterativos, a carga normal crítica que gera a ruptura no topo (e não a perda de instabilidade) fica em torno de NSd = 900 tf, mantendo-se todas as demais condições (vinculações, forças horizontais e momentos fletores no topo).

IMPORTANTE: os valores apresentados anteriormente neste artigo devem ser devidamente verificados, pois não foi feita nenhuma validação cuidadosa dos dados inseridos no sistema. O exemplo anterior foi feito apenas para ilustrar o funcionamento e a abrangência do pórtico não-linear físico e geométrico (NLFG).