GamaZ - FAVT

Mensagem enviada à Comunidade TQS

Aos usuários do TQS,

Gostaria de saber como funciona o cálculo do coeficiente GamaZ e do multiplicador de esforços nos casos em que se tem esforços horizontais importantes além do vento, como excentricidades de carga vertical e empuxos.

Resposta

Já tive a oportunidade de comentar nesta Comunidade, por inúmeras vezes, que o GamaZ é um coeficiente genial para estimar os efeitos de segunda ordem em uma estrutura de concreto armado. É importante lembrar que o GamaZ é fruto da tecnologia nacional e foi criado pelos nossos brilhantes engenheiros estruturais Augusto Carlos Vasconcelos e Mário Franco. Embora genial, com um enorme poder de síntese para medir a sensibilidade da edificação aos efeitos de segunda ordem, ele não é um coeficiente tão fácil de ser compreendido.

Há muito tempo, temos debatido o tema GamaZ, aqui internamente na empresa, principalmente quando ocorrem deslocamentos horizontais no edifício que não são originários da carga horizontal devido ao vento. Estes casos ainda não são contemplados pela NBR 6118:2003.

Para tentar responder à sua pergunta, vamos recordar alguns aspectos importantes do GamaZ e os efeitos de segunda ordem.

A) Originalmente, o GamaZ foi definido para medir o grau de sensibilidade da edificação com relação aos efeitos de segunda ordem. Simultâneamente a esta aferição, o GamaZ também deveria ser utilizado para majorar os efeitos de primeira ordem devido a cargas horizontais para se chegar aos efeitos de segunda ordem finais.

Veremos adiante que esta afirmação acima é válida apenas para determinadas condições.

B) Tenho conhecimento de três métodos básicos para a determinação dos efeitos de segunda ordem (mais comuns):

B.1) Utilizando o método do GamaZ.

B.2) Empregando o método de resolução do pórtico espacial com dois modelos distintos (um vinculado ficticiamente na direção horizontal e o outro liberado, com a aplicação das cargas horizontais devido à vinculação fictícia). Este método está explicado com maiores detalhes na norma brasileira de estruturas metálicas. Neste caso, temos que montar dois pórticos espaciais distintos e ir armazenando os seus resultados. Após a resolução dos dois pórticos para todos os carregamentos, uma correção similar ao Gamaz é aplicada aos esforços do pórtico sujeito apenas às cargas horizontais fictícias. É um método muito interessante que leva a ótimos resultados. Processo muito defensável, embora trabalhoso.

B.3) Utilizando o método do P-Delta. Este é o mais adequado para esse tipo de análise. Mas o P-Delta também tem seus inconvenientes. Em estruturas de concreto armado, é necessário desprezar as deformações axiais devido às cargas verticais, etc. Na versão 13 dos sistemas TQS, melhoramos o método P-Delta já existente com um razoável grau de refinamento com relação a estas estruturas. Acho muito oportuno, com as técnicas atualmente disponíveis, considerar o P-Delta o método mais refinado e confiável para se fazer uma comparação com os resultados do GamaZ. Entretanto, o P-Delta tem outro problema: como medir, em um coeficiente apenas, se a edificação possui um grau elevado de efeitos de segunda ordem? Para resolver isto, criamos nos sistemas TQS uma variável denominada RM2M1, que é equivalente ao GamaZ neste processo P-Delta. Vamos, pois, comparar o resultado médio dos efeitos de segunda ordem pelo processo P-Delta, através deste coeficiente RM2M1, com o método do GamaZ.

C) As edificações ideais para a aplicação do GamaZ praticamente inexistem na prática. Já publiquei aqui, recentemente, um artigo do prof. Vasconcelos sobre casos onde o GamaZ não deve ser aplicado. São quase todos os nossos casos do dia-a-dia.

No mundo real de projetos, as edificações não são simétricas, vigas de transição existem, cargas excêntricas estão sempre presentes, empuxos desequilibrados sempre aparecem, torções do edifício, em planta, também são comuns, etc. Em suma, o edifício se desloca horizontalmente por inúmeros outros efeitos e não apenas pelo efeito de vento.

Como então considerar o GamaZ no mundo real? Para explicar como resolver estes casos, vou apresentar duas alternativas para a consideração do GamaZ, uma que denomino de “teórica” e outra que chamo de “Fator de Amplificação de Esforços (FAE)”.

C.1) Primeira alternativa - GamaZ teórico.

O GamaZ teórico depende apenas da rigidez da estrutura e da carga vertical total para cada carregamento. Portanto, ela independe dos outros efeitos que também deslocam horizontalmente a edificação devido a cargas verticais e empuxos, por exemplo. O GamaZ teórico também é um fator amplificador de esforços para a obtenção dos esforços finais de segunda ordem.

Neste caso, para se chegar aos esforços finais de segunda ordem, devemos multiplicar este valor obtido, que eu denomino de “teórico”, que é também um fator de amplificação de esforços (FAE), por todos os esforços de primeira ordem que provocam os deslocamentos horizontais na estrutura (vento, desaprumo, empuxo, deslocamento horizontal de carga vertical, etc.). Existe uma certa dificuldade na determinação desses esforços de primeira ordem que devem ser considerados.

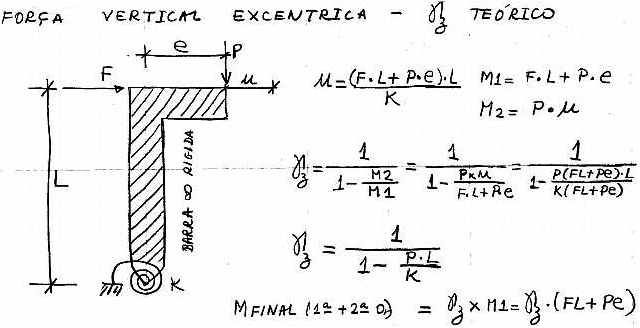
O eng. Francisco Graziano, de maneira genial e muito didática, elaborou um exemplo onde esta dedução do GamaZ teórico pode ser claramente compreendida. O eng. Graziano aplicou a teoria do GamaZ a uma estrutura com uma ou duas barras apenas, barras rígidas, com um coeficiente de mola na base. Peço aqui a permissão ao eng. Graziano para reproduzir a figura educativa conforme abaixo:

GamaZ teórico - Força centrada

“u” é a variável que mede o deslocamento horizontal no ponto de aplicação da carga vertical.

GamaZ teórico - Força excêntrica

C.2) Segunda alternativa - FAE

O Fator Amplificador de Esforços (FAE), simulando o GamaZ, é empregado para a obtenção dos esforços finais de segunda ordem ponderando “apenas as cargas horizontais de vento” atuantes. Este é o método adotado pelos sistemas TQS.

Essa grandeza (FAE) depende, ao contrário do GamaZ, além da rigidez da estrutura e da carga vertical total, dos deslocamentos reais da estrutura devido a estes efeitos de desaprumo, empuxos, excentricidades, etc.

Quando o edifício é perfeitamente simétrico, o GamaZ e o FAE são idênticos. Caso contrário, estes valores não são iguais.

A formulação para este caso é a seguinte (baseado na figura do item acima do eng. Francisco Graziano):

FAE (GamaZ) - Carga excêntrica

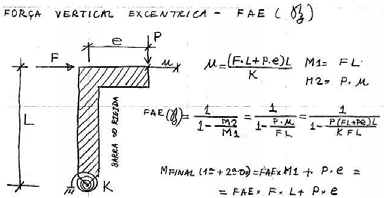
Note que o valor do M1 acima não leva em conta o fator P*e.

C.3) Exemplo

Para melhor entender a diferença entre os dois casos acima citados, vamos calcular algumas grandezas numéricas com este exemplo extremamente simples:

GamaZ teórico - Carga excêntrica

“u” é a variável que mede o deslocamento horizontal no ponto de aplicação da carga vertical.

FAE - Carga excêntrica

Note que o M1 somente considera o momento devido ao vento (carga de 2 tf).

Com o processamento realizado pelo método do PDelta, encontramos um valor para o coeficiente RM2M1 como sendo de 1.324. Este valor é similar ao FAE (1.356) e não ao GamaZ teórico. O momento final na base da barra, considerando a primeira ordem e a segunda ordem pelo P-Delta, foi de 43.256 tf*m. (Prof. Vasconcelos desculpe-me pelas casas decimais).

D) Comparação dos resultados.

Observando o exemplo acima, podemos chegar a algumas conclusões:

D.1) Os valores dos momentos fletores na base da barra para o FAE e o GamaZ teórico não são idênticos mas são próximos. A diferença entre estes momentos calculados pelo FAE e pelo GamaZ teórico foi de 2,2%.

D.2) O valor do FAE (1.356) foi o que mais se aproximou do RM2M1 (1.324).

D.3) O momento final na base do pilar pelo FAE (42.10 tf*m) mais se aproximou do momento final na base do P-Delta (43.256 tf*m). O valor deste momento para o GamaZ teórico foi de 41.16 tf*m. Importante lembrar que os três valores ficaram com valores muito próximos.

D.4) Embora o valor do RM2M1 tenha sido inferior ao encontrado para o FAE, o momento fletor na base do pilar foi maior no P-Delta do que no FAE. Podemos considerar que os valores encontrados no P-Delta são os mais precisos. Devemos lembrar também que o coeficiente RM2M1 é um valor médio para toda a estrutura.

D.5) O deslocamento no topo do pilar foi de: RM2M1: 4.342 cm; FAE: 4.212 cm; GamaZ teórico: 4.116 cm.

E) Justificativa para o emprego do FAE - Fator de Amplificação de Esforços e não o GamaZ teórico.

Para os casos de cargas excêntricas, desaprumo, vigas de transição etc, julgamos que o emprego do FAE é o mais aconselhável por três motivos:

E.1) Geralmente, como no exemplo acima, o FAE, ao contrário do GamaZ teórico, mais se aproxima do RM2M1 obtido pelo P-Delta. Portanto, o FAE é mais confiável para a obtenção dos esforços finais na estrutura.

E.2) Em muitas estruturas reais, o GamaZ teórico fornece valores abaixo de 1.10. Portanto, nestas estruturas, classificadas como de nós fixos segundo a Norma, podemos desprezar os esforços de segunda ordem. Entretanto o FAE (ou RM2M1) chega a valores da ordem de 1.30 (majorando os esforços devido apenas a ação do vento). Será que esta majoração de 30% dos esforços devido a carga horizontal (vento) pode também ser desprezada?

E.3) Limitamos a aplicabilidade do FAE (indiretamente o GamaZ) às estruturas, ao valor de 1.3. Não fazemos esta limitação pelo GamaZ teórico, pois julgamos que em alguns casos ela está contra a segurança. Para valores de FAE acima de 1.3, é melhor utilizar o P-Delta.

F) Comentários finais.

Nos sistemas TQS, totalmente parametrizável, temos um critério para a não consideração dos deslocamentos devido a carga vertical no cálculo do FAE.

O GamaZ que denomino aqui de teórico pode ser encontrado na listagem dos sistemas TQS (Visualização dos parâmetros de estabilidade global) para os carregamentos de vento isolados.

Como o método empregado pelos sistemas TQS é o majorador das cargas horizontais devido ao vento, este deve sempre estar presente no modelo (mesmo que seja uma leve brisa).

Faço aqui uma boa sugestão para os revisores da NBR 6118:2003: incluir o equacionamento do GamaZ para estas estruturas reais que se deslocam horizontalmente por diversos efeitos além do vento.

Espero não ter criado mais dúvidas para os colegas - a mensagem ficou mais longa do que imaginava.

Saudações

Nelson Covas, TQS, São Paulo, SP