Modelos de Cálculo

Conforme estudado nas referências bibliográficas sobre o projeto de reservatórios, onde se citam o livro de Araújo (2010) e as dissertações de Kuehn (2002) e Vasconcelos (1998), existem algumas formas de se modelar e analisar os esforços desse tipo de estrutura. De modo geral, notou-se que procedimento mais empregado é o que foi denominado nesse sistema como "modelo simplificado", que analisa as paredes e lajes de forma independente, mas equilibra, seguindo uma regra, os esforços de interface.

Ainda assim, foi implementado mais dois modelos que levam em conta a ligação monolítica entre as lajes para simular a estrutura com um conjunto único.

Desse modo, é possível definir no editor de critérios o modelo de análise, podendo ser um dos três seguintes descritos a seguir:

df8596edf62b562c5cc74a5b4efa0537.png

Modelo Estrutural

Em todos os casos, é utilizado um modelo de pórtico espacial (nós e barras) para a obtenção dos esforços solicitantes nas paredes e lajes. Este modelo estrutural é montado de modo a simular as características dos três modelos apresentados anteriormente.

Principalmente as restrições de apoio e articulações/restrições das extremidades de barras é que tem variação entre os modelos. Posteriormente serão apresentadas mais pontualmente as diferenças entre os modelos e como o pórtico espacial trata estas diferenças.

Características dos Modelos

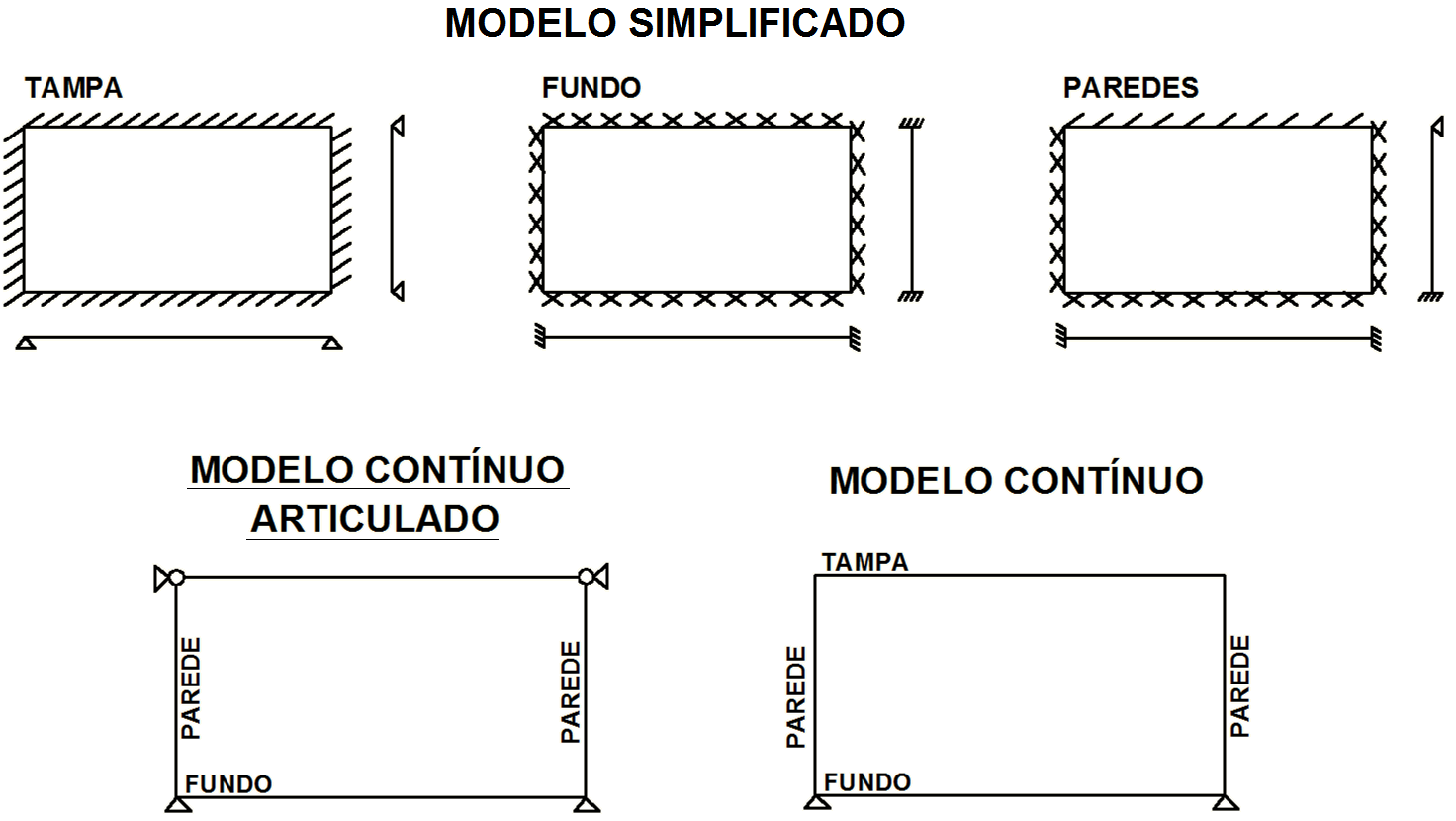
Modelo simplificado

Realizado pelos projetistas em geral, engasta todos os lados das lajes de fundo, engasta os três lados adjacentes entre o fundo e as paredes e o lado entre a parede e tampa é articulada, ou seja, torna-se um apoio fixo. A tampa é definida como totalmente articulada e apoiada nos seus lados.

Nesse modelo, a obtenção dos esforços é obtida de forma desacoplada entre os membros. No presente sistema não é realizado o equilíbrio de momento fletor entre as lajes adjacentes.

Para o cálculo desses momentos, sem o uso desse sistema, é empregado as tabelas de lajes de Bares (1972) ou de Czerny (1976). Mas, no presente sistema, após a geração automática das barras de pórticos espaciais, restringem-se os lados adjacentes.

É sabido que esse modelo simplificado não calcula os esforços normais nas paredes devidos às cargas de empuxo atuantes nas paredes adjacentes, entretanto, esses são computados no sistema conforme descrito em itens a seguir.

Pórtico espacial

O modelo utilizado para a análise estrutural será montado considerando diversas restrições de apoios ao longo da ligação entre as paredes e lajes. Deste modo, a influência do carregamento de um elemento não afeta o dimensionamento dos demais.

Como exemplo, podemos observar abaixo o modo como um modelo de reservatório de uma célula é criado:

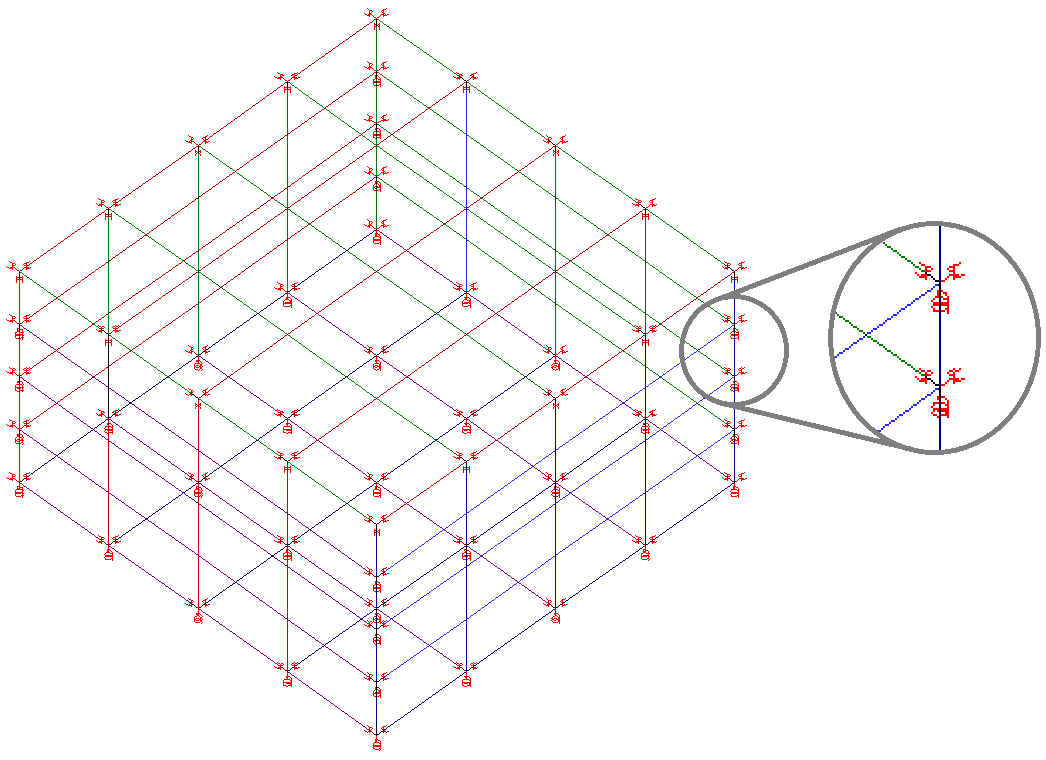
5ce336864b95f85bcba37eb2634dbf5b.png

Neste caso, as restrições de apoio restringem a translação e rotação nas três direções.

Neste modelo, os nós que recebem as restrições de apoio não recebem cargas. Deste modo, as cargas são distribuídas pelos demais nós.

Modelo contínuo

Simula a completa monoliticidade do concreto entre as paredes, tampas e fundos. Os esforços são naturalmente equilibrados, tanto os momento fletores como os normais.

Pórtico espacial

O modelo utilizado para a análise estrutural será montado aplicando restrições de apoio apenas na base (solo, para reservatórios enterrados, ou vértices do reservatório, para reservatórios elevados).

As ligações entre parades/paredes e paredes/lajes são tratadas como contínuas, ou seja, as barras do modelo são ligadas a um mesmo nó.

Como exemplo, podemos observar abaixo o modo como um modelo de reservatório de uma célula é criado:

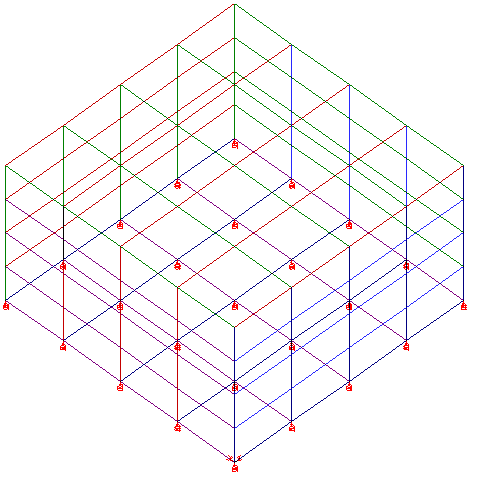
0b9b701b0c9d4034257b930f86cd6655.png

Neste caso, as restrições de apoio restringem apenas a translação vertical dos apoios.

Modelo continuo-articulado

É um modelo intermediário entre o simplificado e o contínuo, definido com continuidade entre as paredes e fundo, mas considerando apoio articulado entre as paredes e a tampa.

Pórtico espacial

O modelo utilizado para a análise estrutural será montado aplicando restrições de apoio apenas na base (solo, para reservatórios enterrados, ou vértices do reservatório, para reservatórios elevados).

As ligações entre parades/paredes e paredes/lajes são tratadas como contínuas, ou seja, as barras do modelo são ligadas a um mesmo nó.

No caso das barras de paredes que se conectam às barras de lajes da tampa, a extremidade é rotulada, de modo que não haja transferência de momentos fletores e torsores entre estes elementos. Os demais esforços (normais e cortantes) são transferidos.

Como exemplo, podemos observar abaixo o modo como um modelo de reservatório de uma célula é criado:

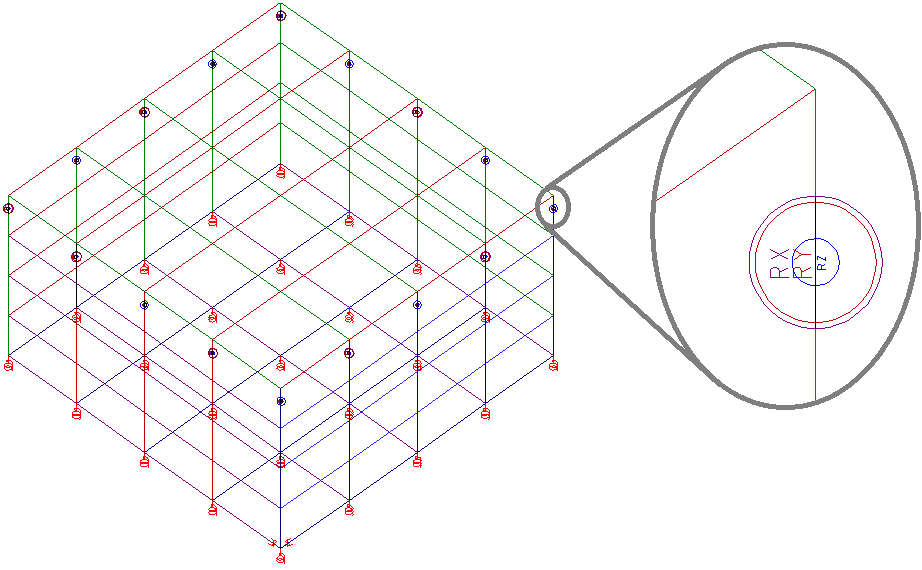
0ce42b35053c49c1251a5b91e63a8952.png

Neste caso, as restrições de apoio restringem apenas a translação vertical dos apoios.

Malha de discretização

O reservatório é modelado automaticamente com o uso de elementos de pórticos espaciais, onde são criadas as malhas das paredes, tampa e fundo de modo que a discretização segue o grau de refinamento conforme definido do editor de critérios nos parâmetros denominados de: “Discretização – Número de divisão em X” e “Discretização – Número de divisão em Y”. Esse número é usado para definir o tamanho do elemento, dividindo o comprimento, largura e /ou altura da célula por esse fator. Limitando o tamanho do elemento em 10 cm.

Dentro desse módulo de edição, define-se a sua geometria, sobrecargas de tampa e fundo, e demais parâmetros que serão descrito a seguir.

Combinações de Carregamento

Reservatórios elevados

Para todos os modelos de reservatórios elevados, têm-se os seguintes os caos considerados:

  • Célula 1 cheia de agua, célula 2 vazia, e com as cargas de peso próprio e sobrecargas;
  • Célula 2 cheia de agua, célula 1 vazia, e com as cargas de peso próprio e sobrecargas;
  • Ambas células cheias de água, não adicionado carga de empuxo na parede 4. Considera todo o peso próprio e sobrecargas;
  • Ambas células vazias, mas com peso próprio e sobrecargas.

Reservatórios enterrados e piscinas

Nesse caso, têm-se nove ou quinze casos considerados para, respectivamente, uma ou duas células.

Uma célula e piscinas

Possui 9 casos:

  • Caso 1: Todas permanentes e célula cheia de água;
  • Caso 2: Todas permanentes e célula vazia de água;
  • Caso 3: Todas permanentes, considera empuxo do solo e célula vazia de água;
  • Caso 4: Todas permanentes, considera empuxo do solo e célula cheia de água;
  • Caso 5: Todas permanentes, considera empuxo do solo e célula cheia de água;
  • Caso 6: Todas permanentes, considera empuxo do solo e do nível de água do lençol freático e célula cheia de água;
  • Caso 7: Todas permanentes, considera empuxo do solo, pressão horizontal (sobrecarga de superfície) e célula vazia de água;
  • Caso 8: Todas permanentes, considera empuxo do solo, pressão horizontal (sobrecarga de superfície) e célula cheia de água;
  • Caso 9: Todas permanentes, considera empuxo do solo e do nível de água do lençol freático, pressão horizontal (sobrecarga de superfície) e célula cheia de água.

Duas células

Possui 15 casos:

  • Caso 1: Todas permanentes e célula 1 cheia de água;
  • Caso 2: Todas permanentes e célula 2 cheia de água;
  • Caso 3: Todas permanentes e ambas as células cheias de água;
  • Caso 4: Todas permanentes e ambas as células vazias de água;
  • Caso 5: Todas permanentes, considera empuxo do solo e células vazias de água;
  • Caso 6: Todas permanentes, considera empuxo do solo e célula 1 cheia de água;
  • Caso 7: Todas permanentes, considera empuxo do solo e célula 2 cheia de água;
  • Caso 8: Todas permanentes, considera empuxo do solo e células cheias de água;
  • Caso 9: Todas permanentes, considera empuxo do solo, pressão horizontal (sobrecarga de superfície) e células vazias de água;
  • Caso 10: Todas permanentes, considera empuxo do solo, pressão horizontal (sobrecarga de superfície) e célula 1 cheia de água;
  • Caso 11: Todas permanentes, considera empuxo do solo, pressão horizontal (sobrecarga de superfície) e célula 2 cheia de água;
  • Caso 12: Todas permanentes, considera empuxo do solo, pressão horizontal (sobrecarga de superfície) e célula 2 cheia de água;
  • Caso 13: Todas permanentes, considera empuxo do solo e do nível de água do lençol freático, pressão horizontal (sobrecarga de superfície) e célula 1 cheia de água;
  • Caso 14: Todas permanentes, considera empuxo do solo e do nível de água do lençol freático, pressão horizontal (sobrecarga de superfície) e célula 2 cheia de água;
  • Caso 15: Todas permanentes, considera empuxo do solo e do nível de água do lençol freático, pressão horizontal (sobrecarga de superfície) e células cheias de água.

Nos casos onde não há empuxo, os casos não serão criados.

Esforços

Momento fletor em cada laje/parede

Com a definição do modelo, para cada caso de carregamento, são obtidos os valores de esforços dos elementos mais desfavoráveis, em cada bordo e direção. Para a avaliação dos momentos fletores, é necessário obter os seus valores por unidade de comprimento, dessa forma, conforme esquema a seguir, esses momentos característicos de cada caso, são obtidos dividindo-se cada momento, advindo do pórtico, pela largura da seção transversal da respectiva laje.


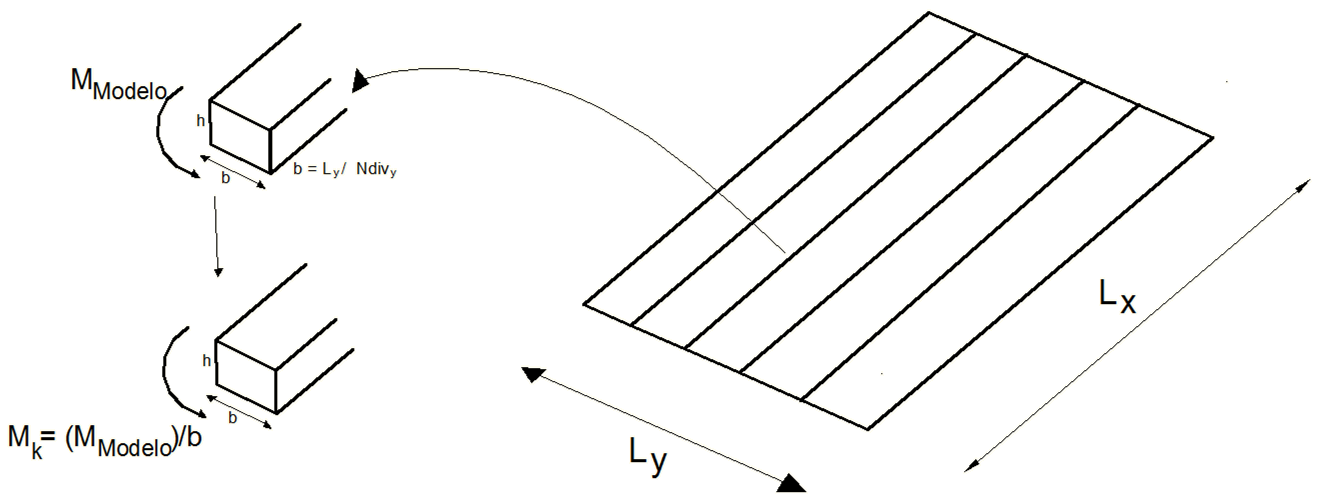
203eeaa492094d1e5705d48ef4df49c6.png

Esforços normais em cada laje/parede

Para o computo dos esforços normais, gerados pelas ações das forcas de empuxo nas paredes, os procedimentos são realizados para cada caso, sendo empregado o caso mais desfavorável.

Modelo simplificado

Os esforços normais são obtidos das reações nos bordos de cada laje, em ambas as direções. Estes são somadas, para obter uma resultante e divididos pela largura do bordo de sua atuação, levando a unidade de força/distância (F/L).

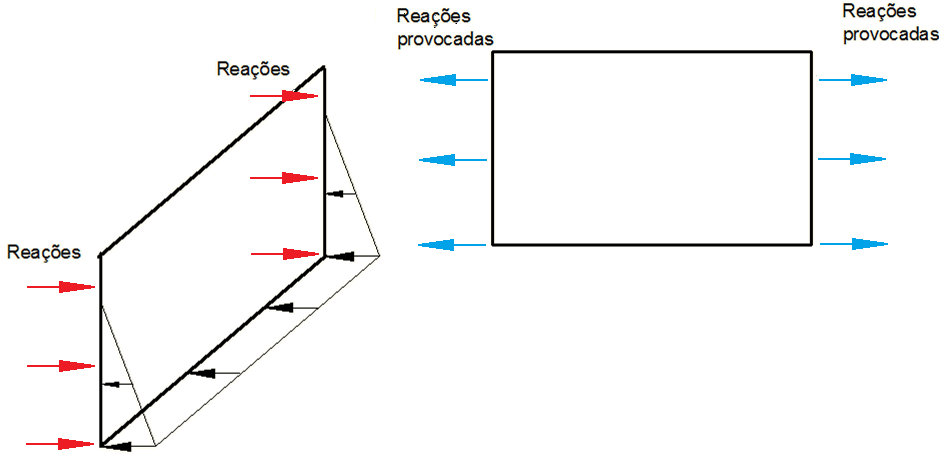
c461a05a175a97887cd93f6d914805f3.png

Modelo continuo e continuo-articulado

Obtêm-se os esforços dos elementos mais desfavoráveis, em cada bordo e direção. Para cada elemento critico é calculado seus esforços dividindo seus valores pela sua largura. Como os elementos tem continuidade entre si, os esforços normais aparecem naturalmente.

Esforços de dimensionamento

Para cada uma das seis 6 posições de cada laje/parede, apresentadas na figura a seguir, procuram-se as barras que tenham os maiores momentos fletores positivo e negativo. Três valores para cada direção, onde paralelo ao lado x, tem-se os esforços a esquerda, meio e direita. E para a direção y, os esforços no bordo inferior, superior e meio.

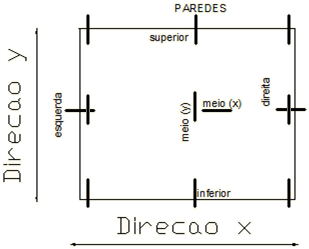
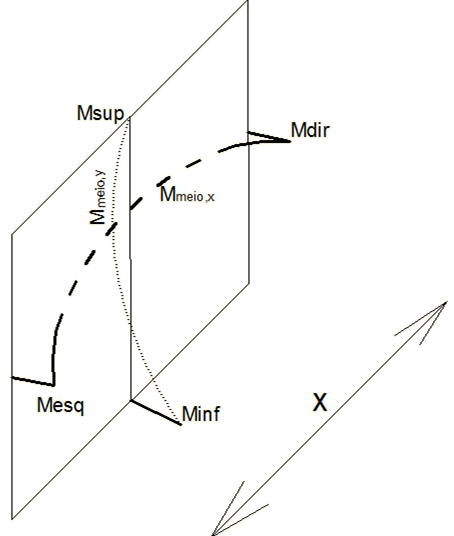
08822a457bcc7f2309a5454db25fc670.png6f438d9ef27dd5f4c5184b989e735caa.png

Adiciona-se o esforço normal médio, para o caso do modelo simplificado, ou toma-se o esforço normal do elemento, no caso dos outros dois modelos, de modo a se obter o maior valor de armadura necessária.

Esse procedimento é feito para cada combinação de carga.

Definição de restrições de apoio quaisquer

Para impor restrições de apoio quaisquer nos reservatórios de forma fácil e rápida:

  • 1. No Gerenciador TQS, selecione a aba "Sistemas"
  • 2. Clique no botão "Elementos Especiais"
  • 3. Na aba "Elementos Especiais ", clique no botão "Editar - Reservatórios "

No programa chamado de Gerenciador de reservatórios:

  • 1. Execute o comando "Apoios";
  • 2. Selecione o tipo de restrição desejado e clique no nó a aplicar tal restrição;

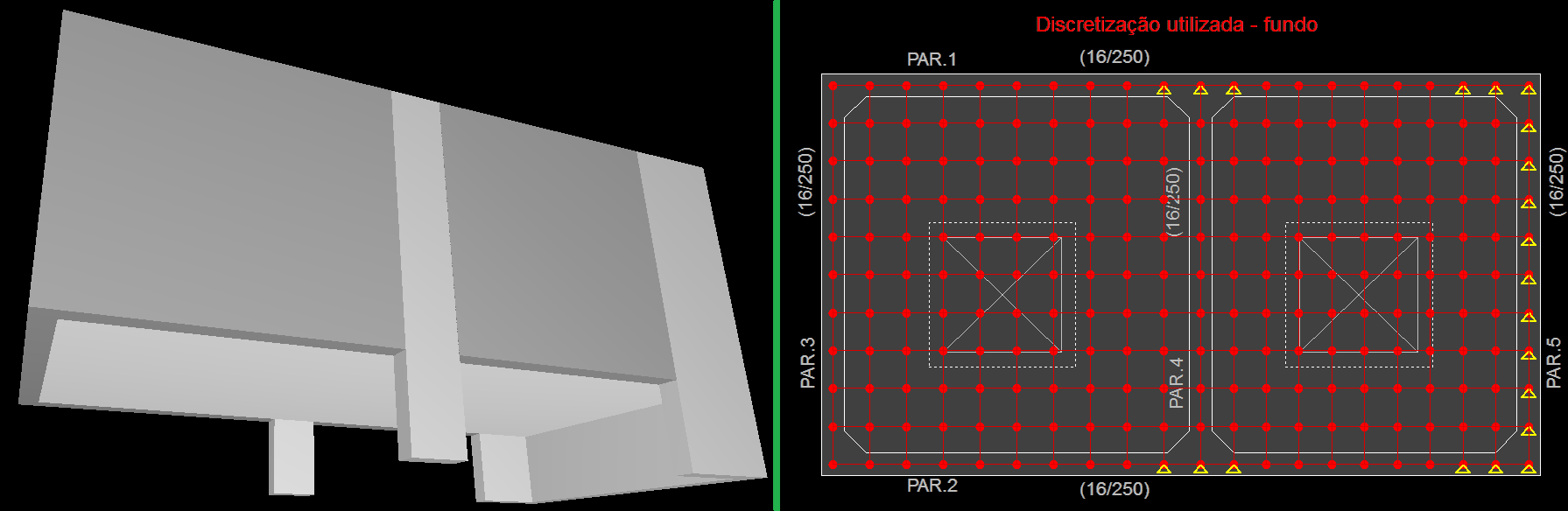
1ddff7e4583af98dd0124be8f3199301.png

Visualização do pórtico

Para visualizar como ficaram os esforços resultantes da discretização selecionada, acione o comando b02e65609c121b597ec8c799b5efc50a.png “Visualizador de esforços” no gerenciador de dados do reservatório.



Dados
Dimensionamento