Capacidade de Carga - Estacas
Modelo de Ruptura Estaca – Solo
Um grupo de estacas forma um complexo sistema por ser formado pelo conjunto de estacas próximas entre si interagindo com o solo, altamente hiperestático pelas condições de contorno, além de ser ligado no topo pelo bloco rígido que normalmente está em contato com o solo. A transferência de cargas ocorre através das interações entre a estrutura (estacas + blocos de coroamento + superestruturas) e os solos adjacentes.
Os mecanismos envolvidos na transferência de carga dependem do modo como a estaca for carregada, ou seja, por esforço axial, lateral, de torção ou pela combinação destes. Estes serão mais complexos quanto mais complicado for o sistema de carregamento.
No SISEs serão consideradas apenas as estacas verticais carregadas axialmente e submetidas a esforços de compressão. Para estacas lançadas com pequenas inclinadas também será feita essa consideração.
A transferência da carga de compressão Ni recebida pela estaca i para o solo, se dá basicamente em duas parcelas:
- ao longo do fuste, devido ao pequeno movimento relativo entre a estaca e o solo, em função do carregamento aplicado, o qual provoca o surgimento de tensões de cisalhamento que dão origem a reação (força) Pl;
- na base da estaca, devido à pressão de contato com o solo, que também depende do movimento vertical da estaca, o qual provoca o surgimento de tensões que dão origem à reação (força) Pp.
A determinação do diagrama de transferência de carga ao longo da estaca-solo depende intimamente de como o sistema comporta no estado de ruptura. Existem vários métodos para a estimativa de ruptura do sistema estaca-solo. Escolheram-se para o SISEs os métodos Aoki-Velloso (1975) e Decóurt-Quaresma (1978), que atualmente são os utilizados e estudados no Brasil.
A seguir são descritos os métodos de cálculo de capacidade de carga lateral e de ponta que estão implementados no SISEs. Na tabela 9.1, indica-se os métodos que são recomendados para cada tipo de estaca, conforme indicado na literatura.
Tabela 9.1 - Métodos indicados para cada tipo de estaca

Método Aoki-Velloso
Este método, com base nos resultados semi-empíricos, estima o diagrama de ruptura do sistema estaca – solo. Inicialmente foi concebido com base nos ensaios de penetração estática CPT, mas através da correlação podem ser utilizados os dados do índice à penetração dinâmica SPT, o mais empregado na atualidade.
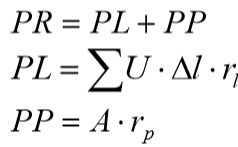
PR: Carga de ruptura do sistema estaca-solo;
PL: Carga de ruptura lateral do fuste da estaca;
PP: Carga de ruptura na base da estaca.
Para:
U: perímetro da seção transversal do fuste da estaca
rl: atrito lateral específico;
A: área da ponta da estaca;
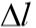 : trecho onde se admite rl constante, sugere-se adotar para cada 1 metro
: trecho onde se admite rl constante, sugere-se adotar para cada 1 metro
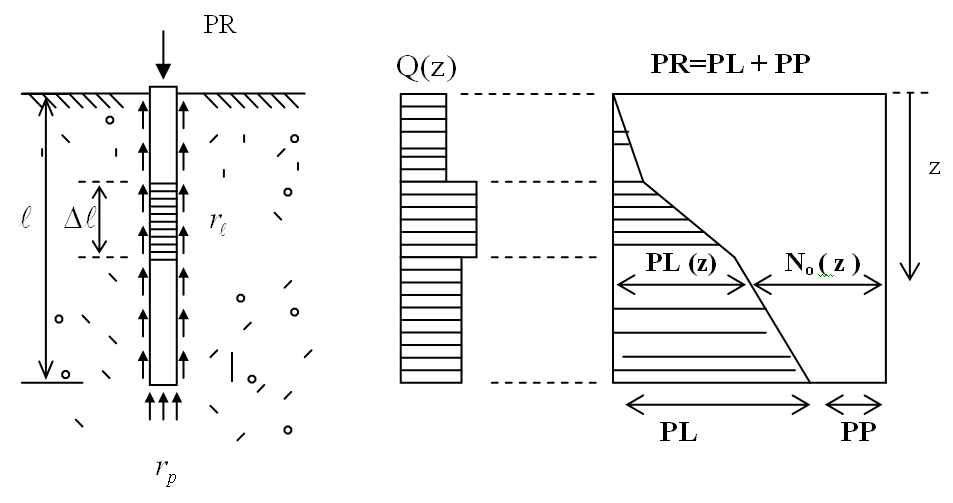
Figura 9.1 – Carga de ruptura do contato estaca – solo.

![]() é o número de SPT obtido nas sondagens à percussão ao longo da profundidade onde será instalado a estaca. O é o atrito lateral específico de um trecho do comprimento da estaca e depende do solo e tipo da estaca empregada. Os valores de e K mais prováveis para os solos da cidade de São Paulo são apresentados na tabela abaixo:
é o número de SPT obtido nas sondagens à percussão ao longo da profundidade onde será instalado a estaca. O é o atrito lateral específico de um trecho do comprimento da estaca e depende do solo e tipo da estaca empregada. Os valores de e K mais prováveis para os solos da cidade de São Paulo são apresentados na tabela abaixo:
| Tipo de Terreno | K ( MPa) | 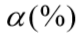 | ||||
| Areia | 1,00 | 1,4 | Tipo de estaca | F1 | F2 | |
| Areia siltosa | 0,80 | 2,0 | Franki | 2,50 | 5,00 | |
| Areia silto argilosa | 0,70 | 2,4 | Pré-moldadas | 1,75 | 3,50 | |
| Areia argilosa | 0,60 | 3,0 | Escavadas | 3,00 | 6,00 | |
| Areia argilo siltosa | 0,50 | 2,8 | ||||
| Silte | 0,40 | 3,0 | ||||
| Silte arenoso | 0,55 | 2,2 | ||||
| Silte areno argiloso | 0,45 | 2,8 | ||||
| Silte argiloso | 0,23 | 3,4 | ||||
| Silte argilo arenoso | 0,25 | 3,0 | ||||
| Argila | 0,20 | 6,0 | ||||
| Argila arenosa | 0,35 | 2,4 | ||||
| Argila areno siltosa | 0,30 | 2,8 | ||||
| Argila siltosa | 0,22 | 4,0 | ||||
| Argila silto arenosa | 0,33 | 3,0 |
Tabela 9.1 – Valores dos coeficientes do Método Aoki-Velloso, ALONSO (1983).
Para estacas pré-moldadas de pequeno diâmetro, o valor F1=1,75 mostrou-se muito conservador. Por isso, Aoki (1985) faz nova proposição para o coeficiente empírico:
![]() , onde D = diâmetro do fuste da estaca em metros.
, onde D = diâmetro do fuste da estaca em metros.
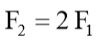
Aoki (1996) comenta que o coeficiente 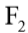 pode variar entre uma a duas vezes o valor de
pode variar entre uma a duas vezes o valor de ![]() e que, portanto,
e que, portanto, ![]() é a hipótese mais conservadora. Para estacas escavadas, segundo Aoki (1976) dependendo do maior ou menor grau de perturbação introduzido no terreno pelo processo empregado,
é a hipótese mais conservadora. Para estacas escavadas, segundo Aoki (1976) dependendo do maior ou menor grau de perturbação introduzido no terreno pelo processo empregado, 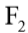 varia entre 4,5 e 10,5 (com
varia entre 4,5 e 10,5 (com ![]() ). Segundo Velloso (1978) apud ABMS (2000) podem ser adotados valores
). Segundo Velloso (1978) apud ABMS (2000) podem ser adotados valores 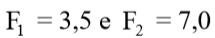 para estacas escavadas com lama bentonítica.
para estacas escavadas com lama bentonítica.
É necessário frisar que os métodos semi-empíricos para o cálculo da capacidade de carga só podem ser aplicados aos tipos de estacas e regiões geotécnicas para os quais foram estabelecidos. Nas outras regiões onde falta caracterização científica, o importante é o levantamento do perfil do solo através da sondagem e determinação do tipo de solo pelo método tato-visual por profissionais experientes e com rigor técnico.
Para o cálculo da carga admissível deverá ser usado um coeficiente de segurança de no mínimo 2:
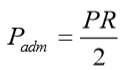
Método Décourt-Quaresma
Este método, ao contrário do método Aoki-Velloso (1975), parte diretamente dos ensaios SPT. Ele foi inicialmente estabelecido em 1978 para estacas pré-moldadas de cravação, mas os autores afirmam que também podem ser aplicados para outras estacas como escavadas, Strauss, Franki, etc. Este método foi revisto em 1982, 1987 e 1996 apud ABMS (2000).
O atrito lateral específico rl é obtida pela fórmula empírica:
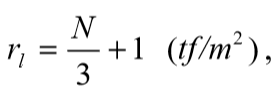
onde 3 ≤ N≤50 em função do número de SPT;
Ou em sistema internacional:
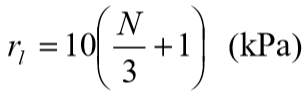
O atrito lateral específico deverá ser multiplicado pela área de contato do fuste da estaca-solo para cada metro de profundidade. O somatório das capacidades laterais ao longo do fuste fornecerá a capacidade lateral acumulada PL.
Inicialmente os valores de número de SPT foram estabelecidos como sendo 3 o mínimo e 15 o máximo. Mas em 1982, o limite superior foi estendido para 50 para estacas de deslocamentos (cravação), embora seja difícil cravar estacas com solos granulares e número de SPT maior que 20. O interessante nesse método, é que para a estimativa de atrito lateral de ruptura, não se distingue o tipo de solo como ocorre em Aoki-Velloso (1975). Mais adiante, veremos que com a introdução de coeficientes ![]() no cálculo de carga admissível é que diferencia entre solos argilosos, siltosos, arenosos e tipo de estaca utilizada.
no cálculo de carga admissível é que diferencia entre solos argilosos, siltosos, arenosos e tipo de estaca utilizada.
Já na resistência da ponta da estaca é estimado segundo tipo de solo:
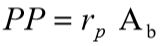
onde: Ab é a área da base da estaca;
rp = C Np (tensão de ruptura da base);
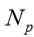 é a média entre os valores de número de SPT na profundidade da ponta da estaca em estudo, o imediatamente acima e o imediatamente abaixo;
é a média entre os valores de número de SPT na profundidade da ponta da estaca em estudo, o imediatamente acima e o imediatamente abaixo;
C é um fator característico do solo, ajustado através de 41 provas de carga realizadas em estacas pré-moldadas de concreto. Nas provas de carga que não atingiram a ruptura, utilizou-se a carga de ruptura convencional correspondente ao recalque de 10% do diâmetro da estaca). Seus valores básicos são:
C= 12 tf/m² para as argilas;
C= 20 tf/m² para os siltes argilosos;
C= 25 tf/m² para os siltes arenosos;
C= 40 tf/m² para as areias.
Décourt (1996) introduziu os coeficientes α e β segundo o tipo de solo e estaca:
| Tipo de solo | Escavada a seco | Escavada (bentonita) | Hélice contínua | Injetadas (raiz) | Injetadas(sob pressão) |
| Argilas | 0,85 | 0,85 | 0,30* | 0,85* | 1,00* |
| Siltes** | 0,60 | 0,60 | 0,30* | 0,60* | 1,00* |
| Areias | 0,50 | 0,50 | 0,30* | 0,50* | 1,00* |
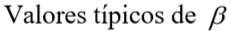 | |||||
| Argilas | 0,80* | 0,90* | 1,00* | 1,50* | 3,00* |
| Siltes** | 0,65* | 0,75* | 1,00* | 1,50* | 3,00* |
| Areias | 0,50* | 0,60* | 1,00* | 1,50* | 3,00* |
* Valores sugeridos diante do reduzido número de dados disponíveis;
** Pode ser considerado também como solos intermediários.
Tabela 9.2 – Coeficientes do Método Décourt-Quaresma, ALONSO (1983).
Décourt (1982) propõe a utilização de quatro coeficientes parciais de segurança referentes às seguintes incertezas: Fp (de parâmetros do solo), Ff (da formulação adotada), Fd (das deformações excessivas) e Fc (das cargas). Para o atrito lateral sugere os valores Fp =1,10 ; Ff =1,00 ; Fd =1,00 ; Fc =1,20 , cuja multiplicação resulta γl =1,10 x 1,00 x 1,00 x 1,20 =1,32, adota-se γl =1,30 e para resistência da ponta Fp=1,35 ; Ff =1,00 ; Fd =2,50 ; Fc =1,20 , cuja multiplicação resulta γp =1,35 x 1,00 x 2,50 x 1,20 =4,05, adota-se γp =4,00.
Então, os coeficientes de segurança “globais” referentes às parcelas de atrito lateral será 1,3 e para a parcela de ponta fica igual a 4,0. Assim a carga admissível deve atender simultaneamente a:
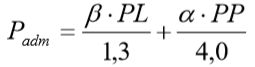
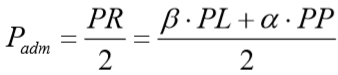
Dentre os dois resultados, deverá escolher a menor dos dois, por exemplo:
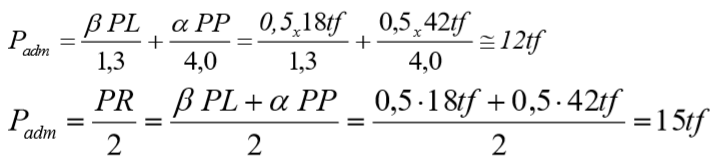
Dado uma estaca escavada a seco num solo arenoso , com PL=18 tf e PP=42 tf, tem-se:
Então, 12tf (a menor) será adotada como carga admissível para as condições do solo e tipo de estaca deste exemplo.
Vale lembrar que estas expressões de cargas admissíveis são de uso exclusivo quando a ruptura lateral (PL) e ruptura na ponta (PP) são estimadas pelo método Decóurt-Quaresma, não fazendo sentido aplicar no método Aoki-Velloso ou nos outros métodos.
Método Antunes e Cabral SEFE III
Tipos de Estacas indicadas: hélice
Método para estimativa de capacidade de carga de estacas, conforme proposto por Antunes e Cabral no SEFE III em 1996 (Seminário de Engenharia e Fundações Especiais e Geotecnia). Este método é bastante empregado para estacas do tipo hélice.
Define-se então o atrito lateral específico ao longo do fuste por:
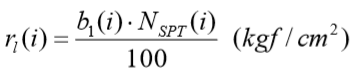
Onde a carga de ruptura lateral ao longo do fuste da estaca é dada por:
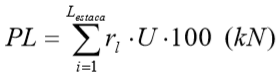
Com:

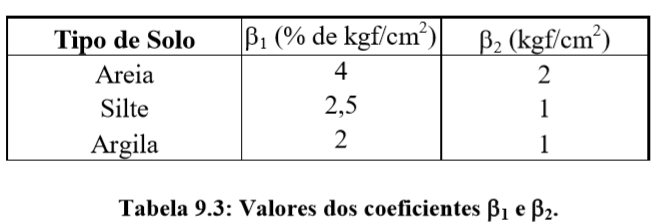
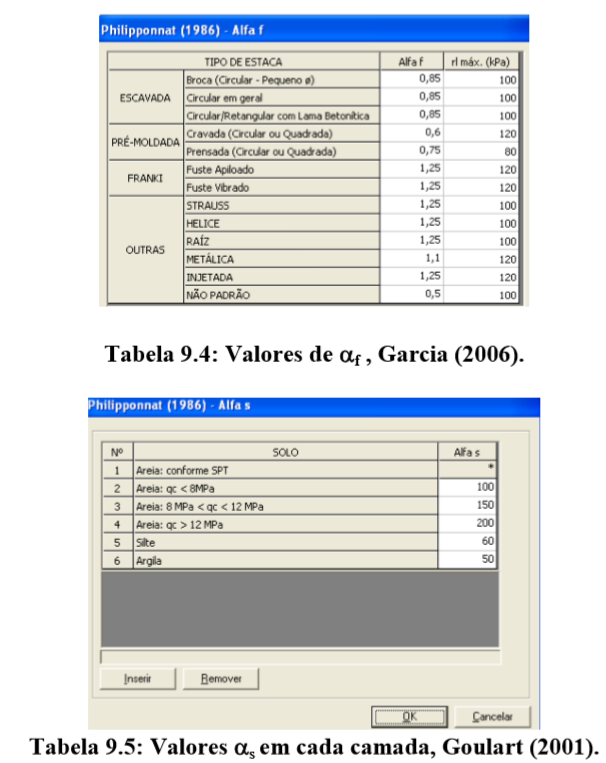
Método Philipponnat
Método semi-empírico. Correlacionado com CPT. O atrito lateral específico ao longo do fuste é dado pela relação:
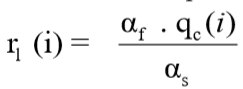
A carga de ruptura lateral ao longo do fuste da estaca é dada por:
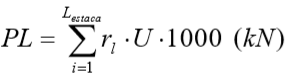
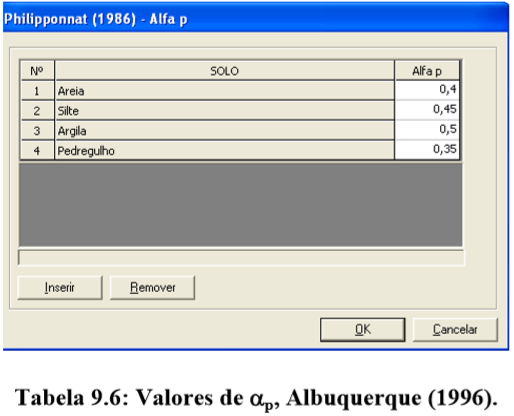
A parcela de tensão de ruptura da ponta é dada por:
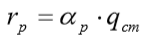
E a carga de ruptura na base da estaca fica:
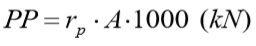
Com qc sendo calculado conforme indicado no método Aoki-Velloso:
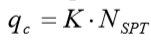
Onde

Método Pedro Paulo Velloso
Método semi-empírico. Correlacionado com CPT.
O atrito lateral específico ao longo do fuste é indicado por:
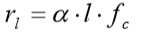
A carga de ruptura lateral ao longo do fuste da estaca fica expressa por:
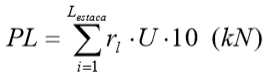
Onde
α: coeficiente indicado na tabela 9.7;
λ: coeficiente indicado na tabela 9.8;
fc é o atrito lateral medido no ensaio de cone, relacionado com o SPT por: 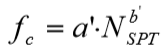 , com Nspt obtido em cda camada do fuste;
, com Nspt obtido em cda camada do fuste;
a' e b' : tabela 9.10;
U: perímetro da estaca.
| Tipo de estaca | α |
| Cravada | 1 |
| Escavada | 0,5 |
Tabela 9.7: Valores de α, Moura (1997).
| Tipo de estaca | α |
| Compressão | 1 |
| Tração (não definido no Sises) | 0,7 |
Tabela 9.8: Valores de λ, Moura (1997).
A parcela de tensão de ruptura da ponta é expressa por:
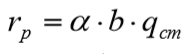
A carga de ruptura na base é indicada por:
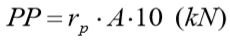
Onde
α: coeficiente indicado na tabela 9.7;
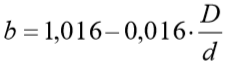 (estacas comprimidas, com D em metros)
(estacas comprimidas, com D em metros)
β=0 (estacas tracionadas);
Se 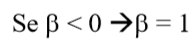 (estacas comprimidas, isto acontece se
(estacas comprimidas, isto acontece se 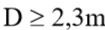 ;
;
D: diâmetro do fuste da estaca;
A: área da ponta da estaca;
d = 0,0356 m = diâmetro da ponta do cone do CPT;
qc é a resistência de ponta é dada por: 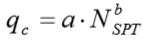
a, b: tabela 9.10;
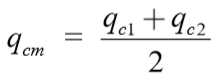
De modo que qc1 é a média de qc de NSUP*D acima da ponta e qc2 é a média de qc de NINF*D abaixo da ponta. Default: Nsup = 8, Ninf = 8, ver tabela 9.9.

Tabela 9.9 Valores de bulbo definidos em arquivos de critérios.
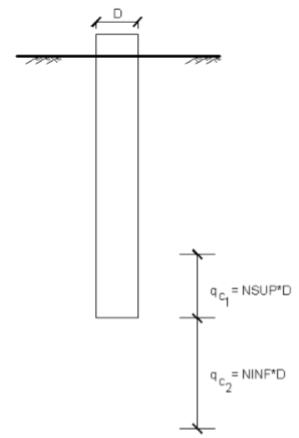
Figura 9.2 - Critério de cálculo de carga de ponta
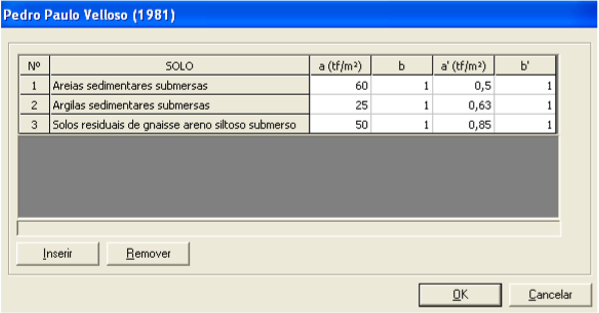
Tabela 9.10: Parâmetros de correlação entre o CPT e SPT de Moura (1997).
Método Alonso
Este método é baseado em medidas de ensaios de SPT-T (sondagem à percussão com medida de torque). Os valores de resistência empregados no método são de torque: Tmáx e Tmín (Tres). Detalhes sobre o ensaio de SPT-T, ver Peixoto (2001).
Conforme Magalhães (2005):
Se entrada de dados for por SPT, correlacionam-se estes com valores de torque (kgf.m) por:
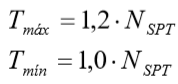
Se entrada de dados for por adesão – atrito lateral (fs) em kPa, converte-se adesão para torque (kgf.m) da seguinte forma:
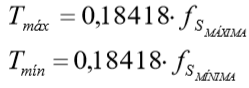
Se entrada de dados for por torque em (kgf.m), então:
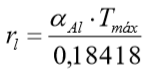
Se 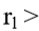 (limites tabela 6.1) →
(limites tabela 6.1) → 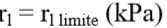
A carga de ruptura lateral ao longo do fuste da estaca é dada por:
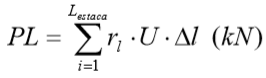
Com
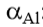 : coeficiente de correção do atrito lateral, ver tabela 9.11;
: coeficiente de correção do atrito lateral, ver tabela 9.11;
U: perímetro da estaca;
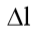 = 1m (considerando que a cada metro da camada rl seja constante);
= 1m (considerando que a cada metro da camada rl seja constante);
| Limite máximo de Torque (kgf.m) | 40 |
| Limite inferior de bulbo | 8 |
| Limite superior de bulbo | 8 |
| R limite (kPa) | 250 |
| Alfa Al | 0,6 |
| Beta Al -> Areia = 250 Argila = 150 Outros= 200 | |
Tabela 9.11: Valores de limites de rl e do coeficiente de correção ![]() por Alonso (1996) para estaca hélice contínua. (fonte Almeida Neto, 2002).
por Alonso (1996) para estaca hélice contínua. (fonte Almeida Neto, 2002).
A parcela de tensão de ruptura da ponta é relacionada com o Tmín (Tres) por:
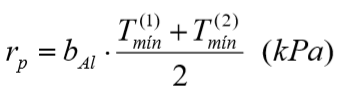
E a carga de ruptura na base é expressa por:
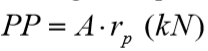
Com 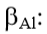 fator de correção, tabela 9.12;
fator de correção, tabela 9.12;
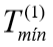 : média aritmética dos valores de torque mínimo (kgf.m) no trecho Nsup*D, acima da ponta, adotando valores nulos caso comprimento da estaca < NsupD;
: média aritmética dos valores de torque mínimo (kgf.m) no trecho Nsup*D, acima da ponta, adotando valores nulos caso comprimento da estaca < NsupD;
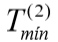 : média aritmética dos valores de torque mínimo (kgf.m) no trecho Ninf*D, abaixo da ponta.
: média aritmética dos valores de torque mínimo (kgf.m) no trecho Ninf*D, abaixo da ponta.
Se 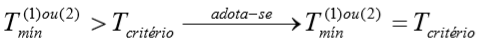
As camadas abaixo da profundidade final da estaca recebem valores iguais da última camada, repetir valores para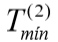 .
.
Como default: Nsup = 8 Ninf = 8
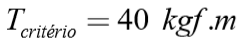
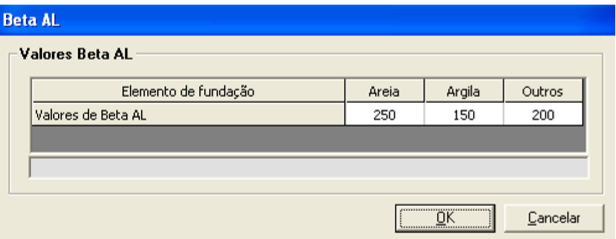
Tabela 9.12: Valores de 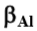 (kPa/kgf.m), Magalhães (2005).
(kPa/kgf.m), Magalhães (2005).
Alonso (1996) enfatiza que estas correlações dependem do local, devendo realizar ensaios de SPT-T e correlacioná-los com SPT de forma estatisticamente adequada.
Método David Cabral
Método semi-empírico específico para estaca raiz. Deve-se conhecer e considerar a pressão de injeção (p) de aplicação de golpes de ar na resistência lateral da estaca. O atrito lateral específico ao longo do fuste é expresso por:
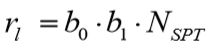
Com 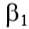 : índice que depende do tipo de solo, ver tabela 9.13;
: índice que depende do tipo de solo, ver tabela 9.13;
D: diâmetro do fuste da estaca em metros;
p: pressão de ar comprimido em kgf/cm²; (entre 0 e 4 kgf/cm²).
![]() sendo dado por: Se estaca raiz, conforme Paschoalin Filho (2008):
sendo dado por: Se estaca raiz, conforme Paschoalin Filho (2008):
Se estaca raiz, conforme Paschoalin Filho (2008):
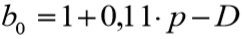
Se 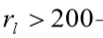
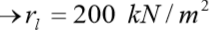
A carga de ruptura lateral ao longo do fuste da estaca é dada por:
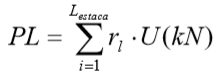
A parcela de tensão de ruptura da ponta é indicada por:
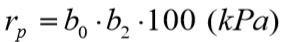
E a carga de ruptura na base é expressa por:
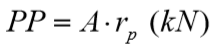
com 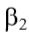 : índice que depende do tipo de solo, ver tabela 9.13;
: índice que depende do tipo de solo, ver tabela 9.13;
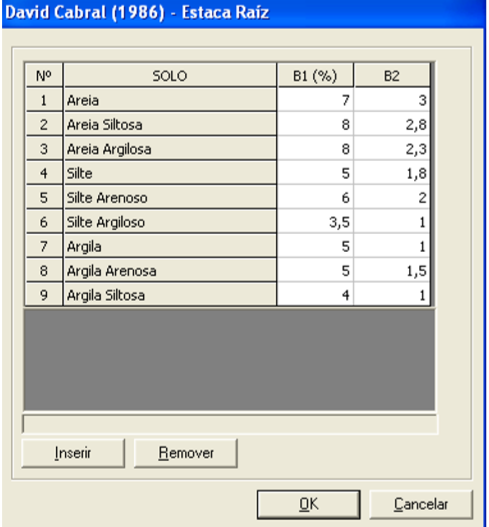
Tabela 9.13: Índices 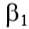 e
e 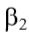 para estaca raiz, conforme Nogueira (2004).
para estaca raiz, conforme Nogueira (2004).
