Recalques em Estacas
Teoria da Elasticidade
A estimativa de tensões e recalques em um ponto no interior do solo, induzido por uma estaca sob carregamento vertical é um problema altamente complexo que envolve vários aspectos como: a interação solo-elemento de fundação, a deformação do solo, a deformação do próprio elemento de fundação, a mudança nas características do solo e das tensões originais, decorrentes da instalação da estaca. Para se proceder ao cálculo da parcela 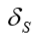 (recalque na base da estaca) deve-se adotar um modelo matemático representativo do comportamento do solo.
(recalque na base da estaca) deve-se adotar um modelo matemático representativo do comportamento do solo.
Segundo VESIC (1975) pode-se lançar mão de três modelos:
a) Função de transferência de carga (curvas t – z);
b) Solução analítica do meio elástico semi-infinito, isótropo, homogêneo, caracterizado pelo módulo de elasticidade (Es) e pelo coeficiente de Poisson (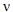 );
);
c) Uso de um modelo numérico: Elementos finitos, Elemento de Contorno, Volumes Finitos, etc.
A adoção do primeiro tipo - que os apoios que o solo oferece são substituídos por molas de rigidez conhecida e obedecendo a lei reológica expressa pela função de transferência de carga; faz crer que um ponto só se desloca se ali for aplicada uma carga. Na realidade, pontos distantes do local carregado, também sofrem deslocamentos, devido à continuidade do meio. Essa continuidade do meio é melhor representado pelos modelos b e c, sendo este ultimo de aplicação pouco difundida devido à dificuldade e alto custo computacional para modelar e analisar o maciço de solo, principalmente levando-se em conta a interação com a super e a infra-estrutura.
A solução de recalques de um grupo de estacas imersas em solo foi apresentada em AOKI & LOPES (1975), como uma extensão de VESIC (1975), através da superposição dos efeitos de cargas no interior do solo utilizando a solução de MINDLIN (1936), segundo o qual as cargas que um grupo de estacas transmite ao terreno são discretizadas em um sistema estaticamente equivalente de cargas concentradas, cujos efeitos são superpostos nos pontos em estudo.
Para o cálculo de recalque imediato, utilizam-se as equações de MINDLIN (1936), considerando o solo como elástico semi-infinito, embora o solo não seja um material perfeitamente elástico, homogêneo e isótropo. Esta equação onde a carga está aplicada em profundidade fornece as expressões das tensões verticais e seus correspondentes recalques. O SISEs aborda apenas a expressão de recalque vertical ![]() .
.
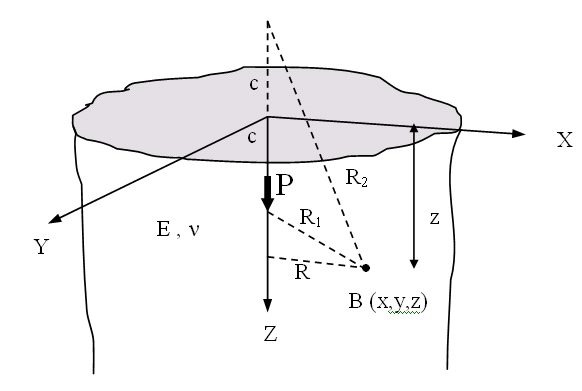
Figura 11.1 – Meio elástico semi-infinito, MINDLIN (1936).
O recalque na profundidade z no ponto B devido a carga pontual P é:
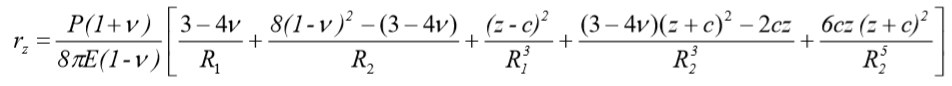
onde:
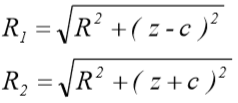
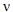 = Coeficiente de Poisson
= Coeficiente de Poisson
E = módulo de deformabilidade do solo, ou modulo de elasticidade;
P = carga aplicada dentro do meio contínuo;
B (x,y,z) é o ponto em estudo, onde se quer saber o recalque![]() .
.
Para o SISEs, são considerados dois modelos para cálculo do recalque para um certo ponto do maciço, o primeiro que apenas leva em consideração a influência das estacas contidas no mesmo bloco, denominado “sem efeito de grupo” e o segundo – denominado de “com efeito de grupo”- que leva em consideração a influência de todas as estacas do projeto, este último mais geral, mas também que demanda um tempo computacional bem maior que o primeiro modelo.
Recalque sem efeito de grupo
Para o cálculo dos recalques da ponta de uma estaca i, a parcela das forças laterais e de ponta desta estaca têm, muitas vezes, mais influencia do que as forças advindas de outras estacas. Assim, este modelo leva apenas e consideração este efeito local. Uma grande vantagem deste é o baixo custo computacional, uma vez que não é necessário avaliar a influência de todas as estacas para o cálculo deste recalque na estaca i. Assim, para um bloco que contem um total de “Nestacadobloco” estacas, a base da estaca i pode se deslocar devido às cargas aplicadas ao longo do fuste Q(z) e ou da ponta Pp. De acordo com Vesic (1975) pode-se escrever:

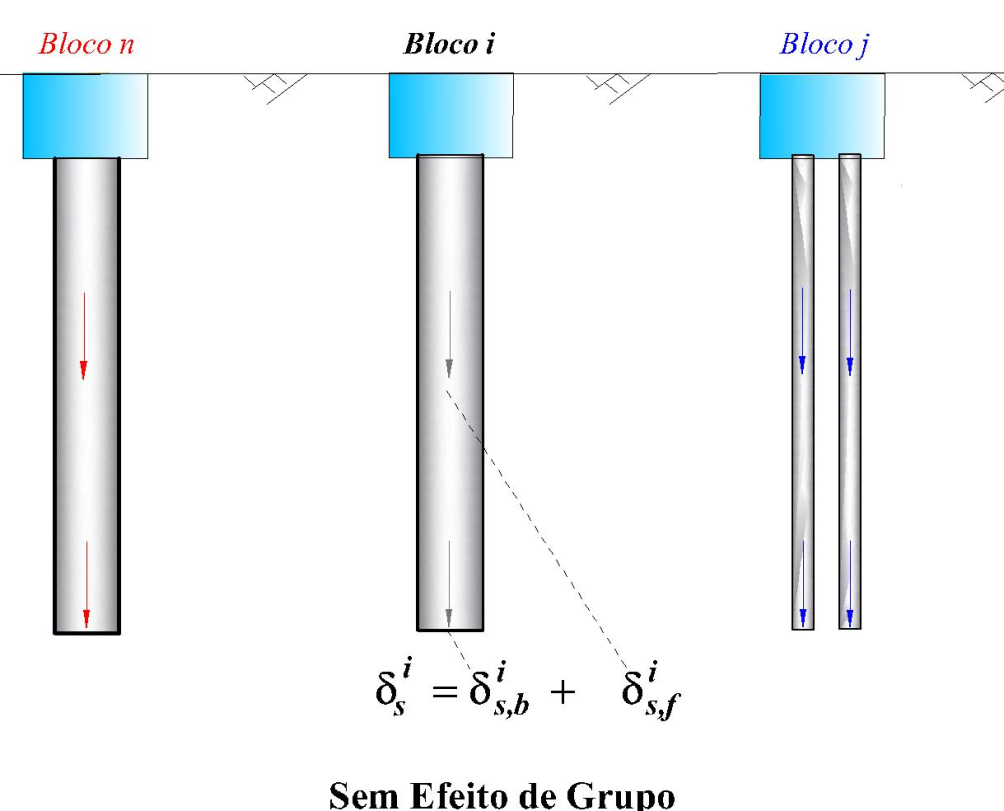
Figura 11.2 – Cálculo de recalque sem efeito de grupo
Recalque com efeito de grupo
Neste caso, o modelo é mais realista, pois leva em conta a influência de todas as estacas do projeto para o computo do recalque da estaca i. Desta forma, a mobilização de uma estaca influencia em todo o maciço contínuo. A desvantagem deste modelo é seu alto custo computacional. Assim, para um projeto que contem um total de “N” blocos, sendo que cada bloco contem “M” estacas, a base da estaca i pode se deslocar devido às cargas aplicadas ao longo do fuste Q(z) e ou da base (ponta) Pp devido a todas as estacas do projeto. De acordo com Vesic (1975) pode-se escrever:

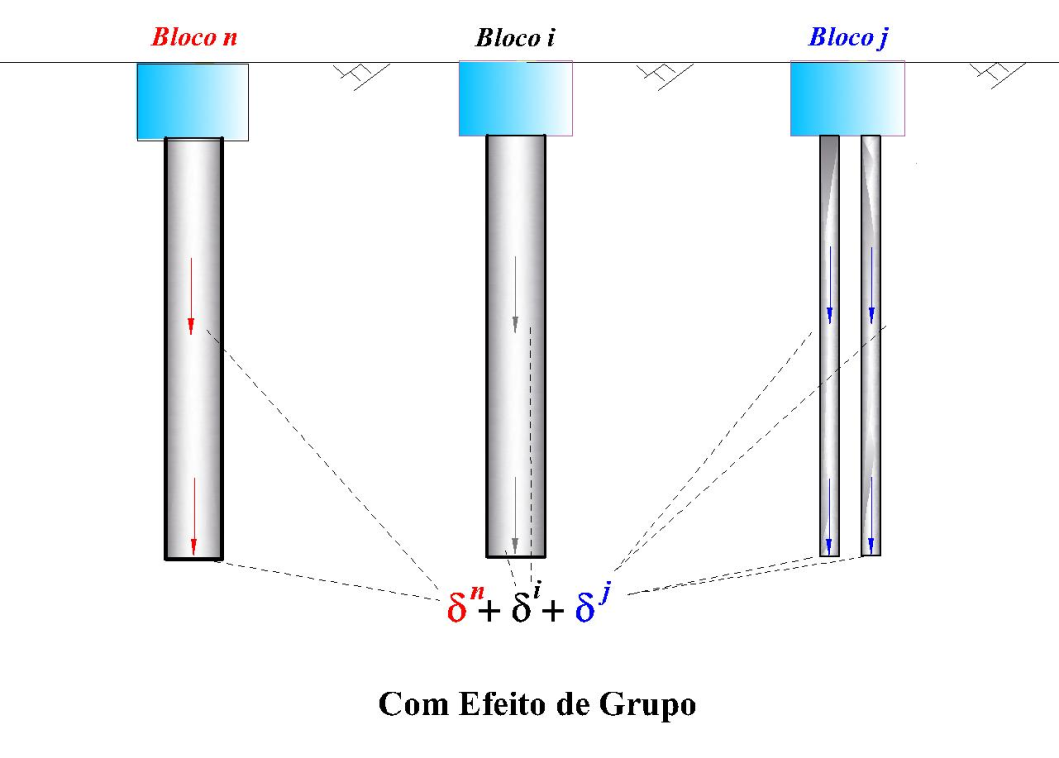
Figura 11.3 – Cálculo de recalque com efeito de grupo
As fórmulas apresentadas por Mindlin (1936) partem da hipótese de que o solo é um meio homogêneo e semi–infinito, o que não corresponde à realidade do solo natural que apresenta estratificação e camada indeslocável em uma determinada profundidade. Para levar em conta estes problemas, pode-se recorrer ao artifício proposto por STEINBRENNER (1934), ainda considerando o solo como semi–infinito e com o uso de MINDLIN (1936) calcula-se:
- o recalque 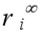 na profundidade “i” no nível entre a superfície e o indeslocável;
na profundidade “i” no nível entre a superfície e o indeslocável;
- o recalque 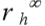 na profundidade “h” escolhido como nível indeslocável.
na profundidade “h” escolhido como nível indeslocável.
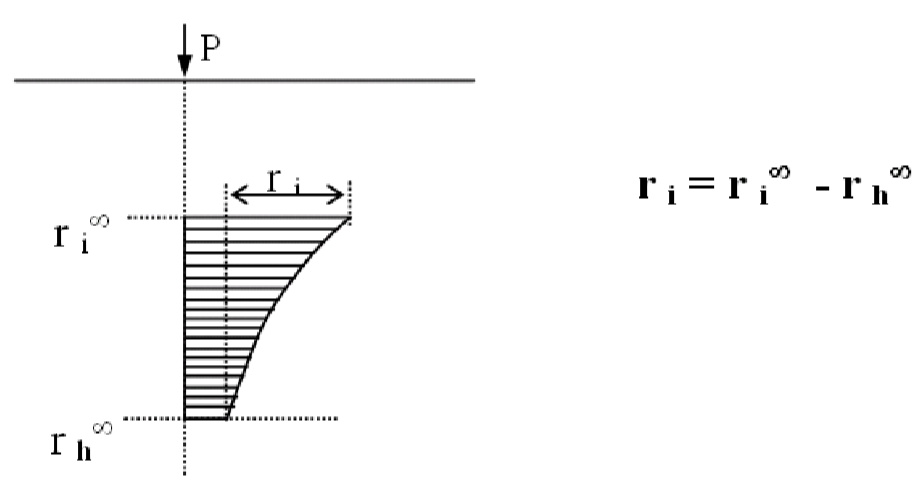
Figura 11.4 – Procedimento de STEINBRENNER (1934).
Como no nível indeslocável o recalque é teoricamente nulo, qualquer recalque no nível “i” que esteja no nível acima será obtido pela diferença entre os recalques dos dois níveis:
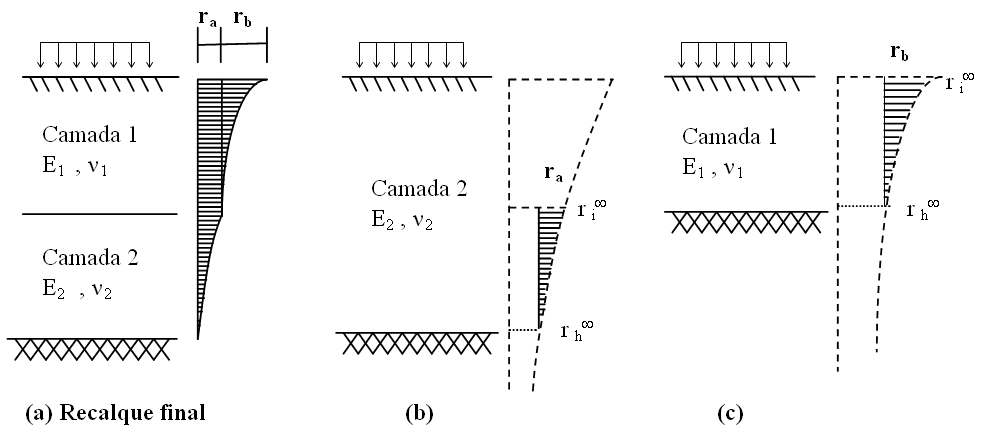
Figura 11.5 – Aplicação do procedimento para várias camadas.
A proposição de Steinbrenner pode ser generalizada para o caso em que existem várias camadas antes do indeslocável. O cálculo é feito da camada de baixo para cima, admitindo-se que todo o solo, do indeslocável para cima, seja do mesmo material da camada 2. Em seguida, calcula-se o recalque 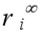 no topo da camada 2 e
no topo da camada 2 e 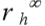 no nível do indeslocável. O recalque nesta camada será
no nível do indeslocável. O recalque nesta camada será ![]() :
:
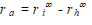
O procedimento é repetido, levando-se o indeslocável para o nível da camada já calculada e utilizando-se as características do solo imediatamente acima calculando o recalque 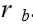 . O recalque no nível da aplicação da carga será obtido pela superposição dos recalques
. O recalque no nível da aplicação da carga será obtido pela superposição dos recalques ![]() das camadas.
das camadas.
Aplicando o mesmo raciocínio para caso de estacas imersas no solo, tem-se:
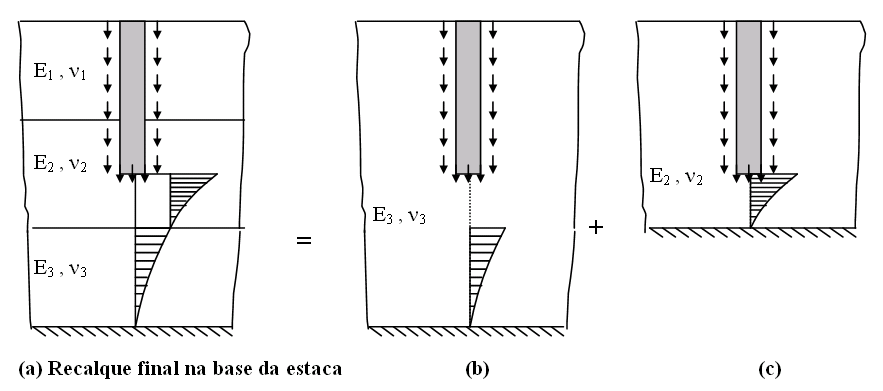
Figura 11.6 – Procedimento de STEINBRENNER para estacas.
Onde se determina para cada nível da camada o correspondente ![]() com características daquela camada em estudo. Portanto, o recalque
com características daquela camada em estudo. Portanto, o recalque 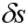 é o somatório de todos os recalques de n camadas abaixo do nível da base da estaca, lembrando-se que os recalques na base da estaca devem levar em conta os efeitos de outras estacas j além da própria estaca i. Feito isso, o recalque no topo da estaca i é a soma do recalque na base da estaca
é o somatório de todos os recalques de n camadas abaixo do nível da base da estaca, lembrando-se que os recalques na base da estaca devem levar em conta os efeitos de outras estacas j além da própria estaca i. Feito isso, o recalque no topo da estaca i é a soma do recalque na base da estaca 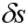 e o deslocamento do fuste
e o deslocamento do fuste 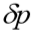 :
:
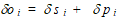
A validade do processo que utiliza STEINBRENNER (1934) é comprovada em alguns trabalhos; entre eles destaca-se o relatório apresentado em KUSAKABE et al. (1989).
Módulo de Elasticidade do Solo
Estimar o módulo de elasticidade (o termo correto para o solo é módulo de deformabilidade) é um dos assuntos mais difíceis da engenharia de fundação. Por sua natureza de material heterogêneo, o módulo de deformabilidade do solo varia conforme o nível de carregamento aplicado, saturação e de região onde está sendo utilizado. Uma formulação que vale para uma região pode não valer mais na outra. A sua escolha correta é o que determina a estimativa de recalque o mais próximo da realidade. Seguem-se algumas fórmulas e tabelas para estimar a ordem de grandeza:
| SOLO | VALORES TÍPICOS(kgf/cm²) |
| Silte arenoso residual de São Paulo | E = 1,15 Rp |
| Silte argiloso residual de São Paulo | E = 2,40 Rp |
| Aterro compactado de silte argiloso | E = 3,00 Rp |
| Areia normalmente adensada | E = 5 (SPT + 5) |
| Areia sobreadensada | E = 180 + (7,50 SPT) |
| Argila terciária de São Paulo | E = 55,4 + (25,9 SPT) |
| Argila muito mole (nº. SPT ≤ 2) | 10 |
| Argila mole (nº. SPT 3 a 5) | 20 |
| Argila média (nº. SPT 6 a 10) | 50 |
| Argila rija (nº. SPT 11 a 19) | 80 |
| Argila dura (nº. SPT > 19) | 150 |
| Areia fofa (nº. SPT ≤ 4) | 50 |
| Areia pouco compacta (nº. SPT 5 a 8) | 200 |
| Areia medianamente compacta (nº. SPT 9 a 18) | 500 |
| Areia compacta (nº. SPT 19 a 40) | 700 |
| Areia muito compacta (nº. SPT > 40) | 900 |
Tabela 11.1 – Estimativas de módulo de deformabilidade do solo, PENNA (2004).
Na Tabela 11.1, Rp é a resistência do terreno ao avanço da ponta de cone, em unidade de tensão (kgf/cm²), força dividida pela área do cone, de 10cm². Além dessa tabela, para solos arenosos, MELO (1971) apud ALBIERO (1993) apresenta uma expressão empírica para previsão do módulo de deformabilidade ES em função do número do SPT:
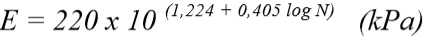
Onde N é o número de SPT da sondagem.
Diferentemente do módulo de deformabilidade do solo, o coeficiente de Poisson tem pouca influência para o recalque. Quanto aos valores do coeficiente de Poisson, têm-se as seguintes estimativas:
| SOLO | POISSON |
| Argila saturada | 0,50 |
| Argila não-saturada | 0,30 |
| Areia | 0,35 |
| Silte | 0,30 |
Tabela 11.2 – Estimativa dos coeficientes de Poisson do solo, PENNA (2004).
Modelo de Distribuição de Cargas Pontuais na Estaca
A idéia básica utilizada pelo sistema SISEs é distribuir as cargas no fuste e na ponta (base) da estaca em cargas estaticamente equivalentes, de modo que represente o mais próximo possível a realidade da obra. Dentro deste conceito, quanto maior a discretização feita, melhor será a representatividade dos resultados.
Carga na base
A carga na base da estaca é admitida como sendo uniformemente distribuída, sendo transformada em um sistema estaticamente equivalente de cargas pontuais atuando em cada uma das subáreas divididas em n1 x n2 partes iguais. Sendo n1 (nº de divisões da circunferência) e o n2 (nº de divisões do raio da base Rb).
Carga no fuste
Para a carga no fuste da estaca admite-se uma distribuição linear. A circunferência, de raio Rs é subdividida em n1 partes iguais e o trecho do fuste entre as profundidades (D2 - D1) é subdividido em n3 partes iguais. Sendo i,k os índices da posição do ponto 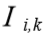 da superfície do fuste.
da superfície do fuste.
