CRV – Estacas

Cálculo de CRV para Estacas e Tubulões

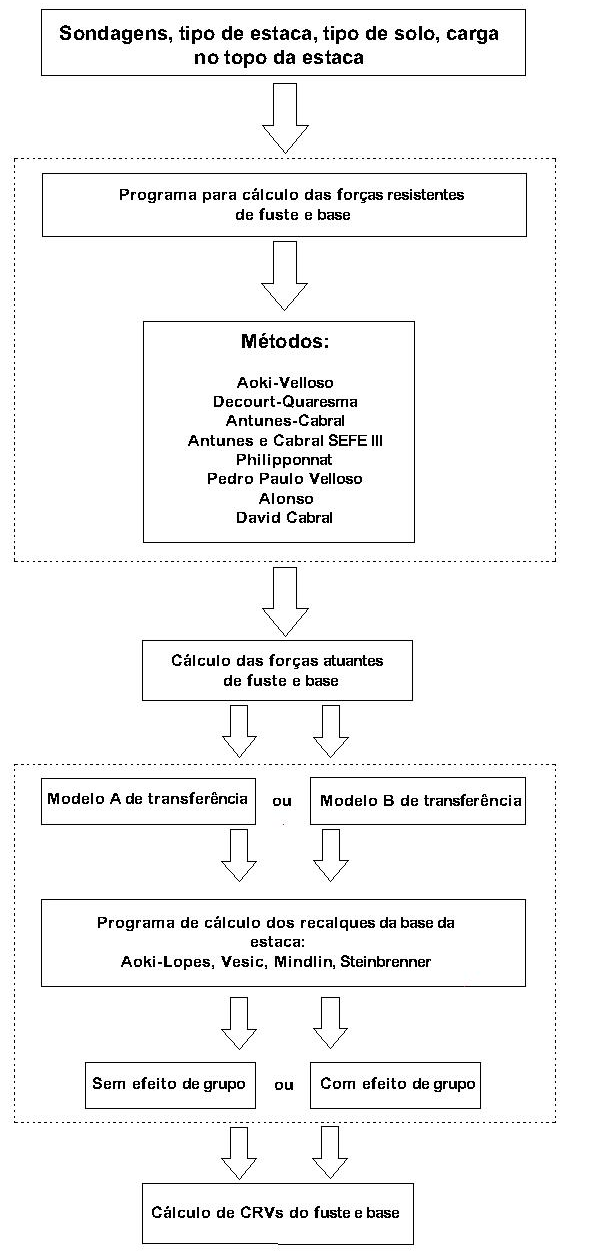
Figura 12.1 – Fluxograma geral de processamento e transferência de dados.

O CRV (coeficiente de reação vertical) pode ser entendido como rigidez do contato estaca-solo. Aplica-se no topo de cada estaca Pi o carregamento obtido pela resolução de pórtico espacial, considerando inicialmente como apoiado em base rígida. O CRV da estaca é a razão entre a carga aplicada no topo e o deslocamento sofrido na base da estaca 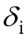, que pode ser resolvido pelo modelo de Aoki-Lopes, com efeito de grupo:

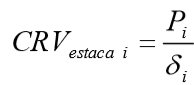
Onde Pi é carga aplicada no topo da estaca e 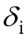é o recalque na base da estaca mais a parcela de deslocamento elástico da estaca (se considerado).

Levando-se em consideração a proporcionalidade das forças distribuídas ao longo do fuste e na base da estaca, pode-se fazer seguinte relação:

Para o Coeficiente de reação vertical do fuste na profundidade j da estaca i, tem-se:

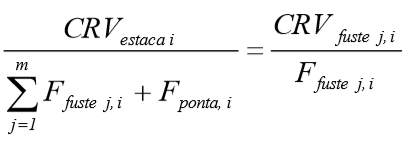
ou seja

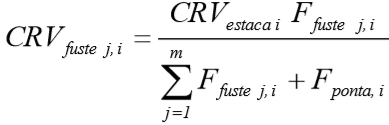
Na expressão acima, a distribuição das forças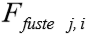 ao longo do fuste, depende do modelo de transferência (modelo A ou B) que for adotado, quando P<PL(z). O denominador 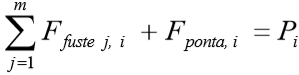pode ser entendido como carga atuante no topo da estaca. Caso esta carga seja menor ou igual a resistência lateral acumulada do fuste PL, pela teoria de VESIC(1975), fica entendido como todo o carregamento resistido pelo fuste, tornando a parcela de carga na ponta (base) zero, .

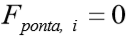Para o Coeficiente de reação vertical da ponta da estaca i, tem-se:

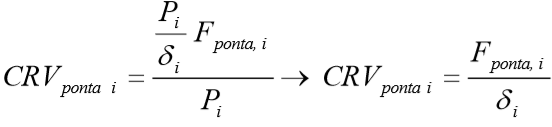
Caso o carregamento aplicado no topo da estaca for todo absorvido pelo fuste, ou seja, 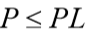, não terá carga na base da estaca, 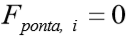, portanto .

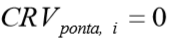O somatório dos coeficientes de reações verticais do fuste e da ponta deverá resultar em coeficiente de reação da estaca i:

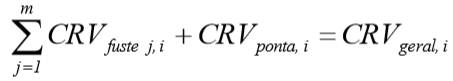
Onde j = 1 , 2, 3, ... , m da estaca i

Fisicamente, a expressão acima pode ser entendida como um conjunto de “molas” que se distribuem ao longo do fuste e na base da estaca, e que estas “molas” representam proporcionalmente a distribuição de rigidezes do contato estaca-solo segundo a lei de transferência de cargas. Isso significa que se for adotado o modelo A de transferência, o carregamento será distribuído começando do topo em direção à base, onde cada “mola” será solicitada por um carregamento e caso atingir a sua plastificação será repassado para “molas” subseqüentes. Neste modelo, a carga na base da estaca só será mobilizada caso todo o contato fuste-solo atinja a sua plastificação (deslizamento). Caso for adotado o modelo B de transferência, o carregamento será proporcionalmente distribuído ao longo do fuste, e como no modelo A, só será transferido para a base da estaca quando toda a resistência lateral da estaca for vencida pelo carregamento aplicado no topo, ou seja, quando entra em plastificação.

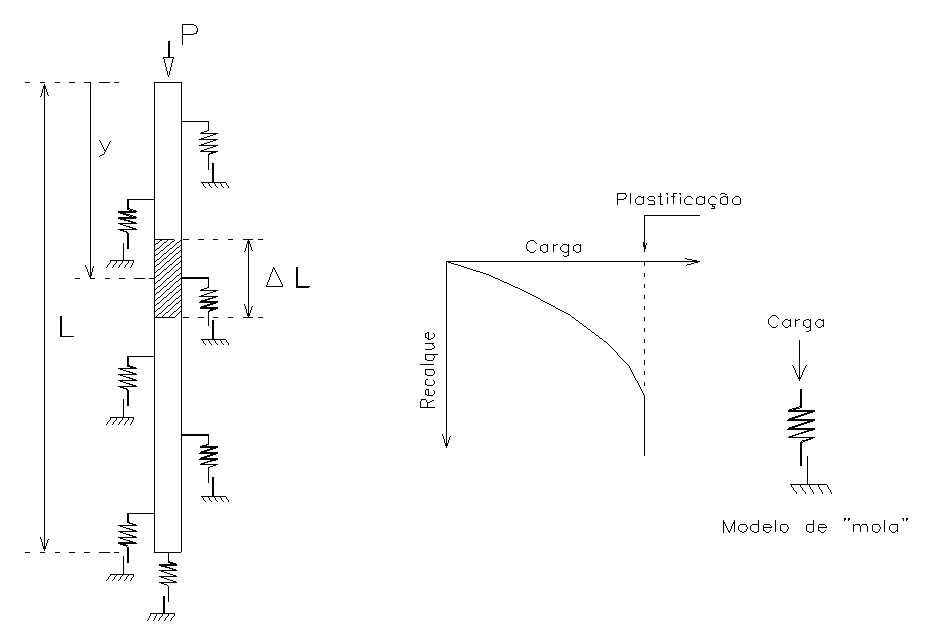
Figura 12.2 – Representação da estaca.

Vale ressaltar que o “trunfo” deste modelo é a sua simplicidade em relação aos modelos mais sofisticados (método dos elementos finitos ou elementos de contorno), facilitando sua aplicação e a representatividade. A “mola” idealizada não é a mola de Winkler, pois:

- ela varia conforme o nível de carregamento, inclusive altera a curva quando o carregamento ultrapassa a resistência lateral PL do fuste. Portanto, a “mola” representa a não linearidade do comportamento da estaca;

- ela é influenciada pelo efeito de grupo de estacas, ou seja, o carregamento de uma estaca influenciará nos recalques das demais estacas próximas.

Pontua-se ainda que não existe coeficiente de mola constante para um determinado solo. O seu valor depende da interação completa da rigidez da estrutura x solo. Por exemplo, os coeficientes de mola da fundação de um edifício sobre o solo “A” não são os mesmos se for construído sobre esse mesmo solo um edifício com outra rigidez (número de pavimentos, arranjos estruturais ou sistemas estruturais diferentes).

Na figura 12.3 apresenta-se esquematicamente o procedimento descrito nesse item, destacando que é possível incluir ou não, conforme habilitado no arquivo de critérios, o deslocamento axial (De) da estaca para o computo do recalque total.

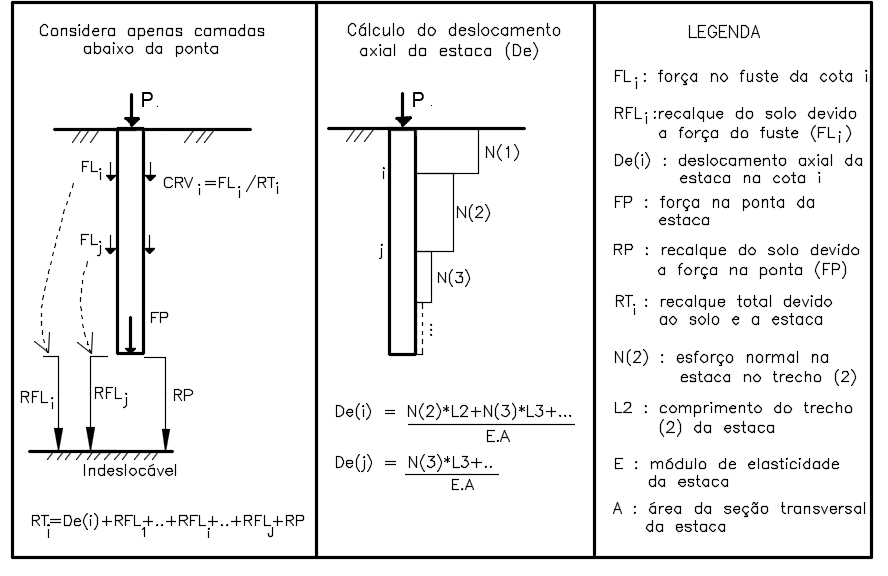
Figura 12.3 – Fluxograma geral de processamento e transferência de dados.

Ao processar o Sises, o relatório sobre CRV/CRH pode ser acessado em Visualizar Cálculo dos CRV e CRH "SEstCrvh.lst". Ele apresenta o layout indicado na figura 12.4, onde nas figuras 12.5 e 12.5 se amplia para uma melhor visualização. Nesse relatório é possível organizar as informações em 4 sub-blocos, indicados por A, B, C e D, vide fig. 12.4.

No sub-bloco A têm-se os valores em cada cota, de metro em metro, do módulo de elasticidade, coeficiente de Poisson e dos parâmetros K e alfa do solo relativos - nesse caso- ao método de Aoki-Velloso.

No quadro B, apresentam-se os valores de Capacidade de Carga obtidos com os dados e para o método definido, onde PL, PP e PTOTAL são, respectivamente, carga no fuste, ponta e a soma dessas.

No sub-bloco C, apresentam-se os valores das transferências de fuste (FLi) e de ponta (última linha da coluna de FLi). Note na fig. 12.5 que a soma das forças que foram transferidas ao solo, pelo fuste, é de 10,68 tf enquanto que a parcela de ponta tem um valor transferido de 6,18 tf, o que resulta na transferência total da força vertical de topo (16,86 tf). O recalque total em cada metro (RecTotal) é obtido somando o valor do recalque total do fuste (RecFuste), com o valor do recalque de ponta (RecPonta) mais o deslocamento axial da estaca em cada metro (DeslAxial), ou seja, na 1a. cota seria de RecTotal (1) = 0,132+1,443+0,128 = 1,703 cm; ou RecTotal (2) = 0,132+1,443+0,112 = 1,687 cm; etc.

O conceito do recalque corrigido (RecCorrig) é relativo a uma penalização do recalque total sofrido caso o valor da força vertical de topo seja maior que a de ruptura, simulando uma variação acentuada do recalque no regime plástico e com deslizamento acentuado pós carga de ruptura. Nessa filosofia, adotou-se a seguinte majoração para o recalque total:

Para o sub-bloco D, têm-se os valores dos coeficientes de mola a serem lançados nos nós das estacas discretizadas. Assim, para exemplificar, empregando os resultados indicados nas figuras 12.5:

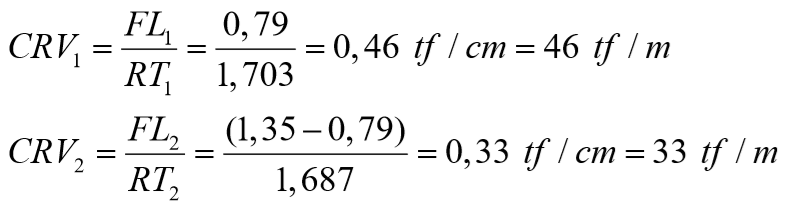
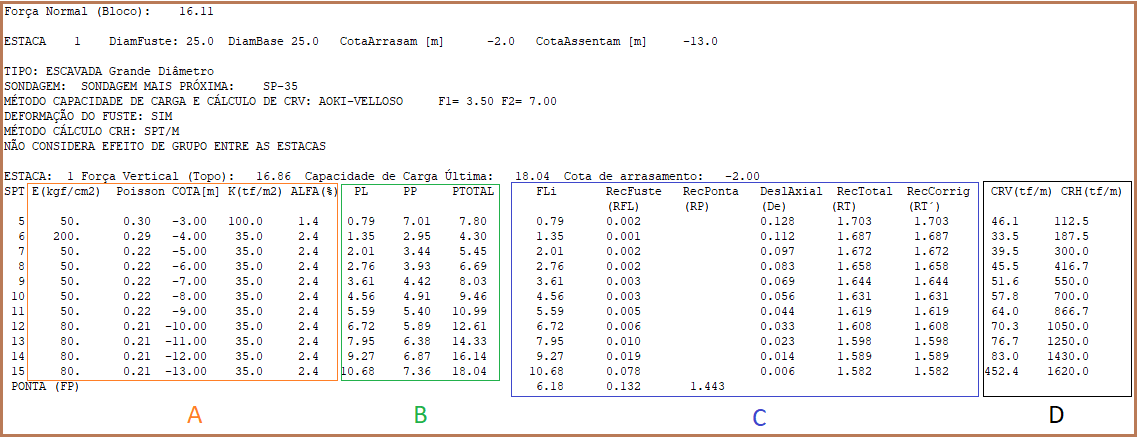
Figura 12.4 – Esquema do relatório dos CRV/CRH.

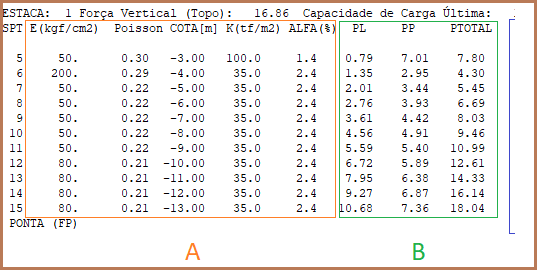
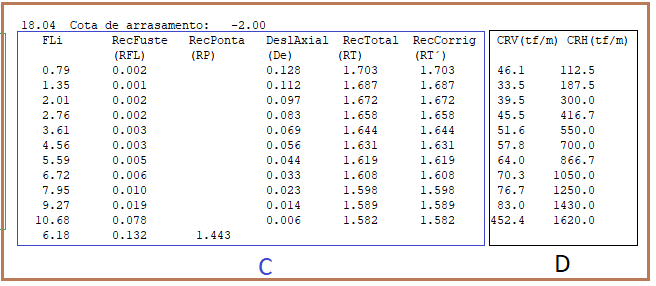
Figura 12.5 – Esquema do relatório dos CRV/CRH ampliado.

Observações Sobre o CRV

O método Aoki e Lopes (1975) à luz da teoria da elasticidade com o uso de solução de Mindlin (1936) e processo de Steinbrenner(1934) tornou possível a análise dos efeitos de ações de grupos de elementos de fundações, sem a necessidade de discretização do meio envolvente (maciço de solo), como é feito mediante o uso do Método dos Elementos Finitos. Porém a transferência de cargas para o solo adjacente é feita como se fosse meio contínuo, incluindo o espaço preenchido pelas estacas, não considerando a descontinuidade do maciço. Esta ‘lacuna’ só é resolvida com o uso de ferramentas mais sofisticadas como a combinação de método dos elementos de contorno e método dos elementos finitos discretizando tanto o maciço de solo como elementos de estacas para simular a existência de diferentes materiais (estaca x solo) e a introdução de elementos de contato para simular o deslizamento relativo estaca/solo.

Seria interessante verificar mediante a comparação dos dois métodos, se esta descontinuidade ocupada pelas estacas até que ponto é realmente significativa ou não. Também é importante enfatizar que nem todos os resultados numéricos mais ‘sofisticados’ são verdadeiros para o uso prático, pois o solo é um material que dificilmente se pode simular com realismo, devios a suas intrinsecas características de dificl mensuração e simulação numérica.

Outra simplificação do modelo é o diagrama de transferência de carregamento da estaca ao longo do fuste. A resistência máxima do contato fuste – solo pode mudar com o efeito do grupo de estacas devido à deformação do solo adjacente provocados pela interação do conjunto. Este efeito é de difícil quantificação, e no momento não está sendo considerado no modelo.

Após alguns testes com as rotinas de cálculo, chegou-se a seguinte conclusão:

- quanto menor o número de subdivisões (n1, n2, n3), menos precisão terá os recalques nos pontos desejados. Do contrário, quanto mais discretizado, melhor será a representação da distribuição de cargas na estaca, pois o nosso objetivo é tentar simular a integração numérica através de subdivisões.

- o processo possui convergência, ou seja, após certo número não há mais melhora dos resultados. Por “default” o sistema opera com valores n1 = 8, n2 = 4 e n3 = 30, por apresentarem resultados satisfatórios.