Blocos sobre Estacas

Para verificar blocos sobre uma estaca, a verificação das tensões nos blocos de concreto e o dimensionamento das armaduras são baseados no método de Blèvot ou dois métodos baseados em (Fusco, 1994).

Para verificar blocos de 2 a 7 estacas, a verificação das tensões nos blocos de concreto e o dimensionamento das armaduras são baseados no método de Blèvot, dois métodos baseados em (Fusco, 1994) ou MBT (método das bielas e tirantes) comentários do Ibracon (ABNT NBR 6118:2014 Comentários e exemplos de aplicação, 2015).

Para verificar blocos de 7 a 24 estacas, a verificação das tensões nos blocos de concreto e o dimensionamento das armaduras são baseados no método de Blèvot, dois métodos baseados em (Fusco, 1994), MBT (método das bielas e tirantes) comentários do Ibracon (ABNT NBR 6118:2014 Comentários e exemplos de aplicação, 2015).

ou no método do CEB-FIP.

Capacidade de carga nas estacas

Para dimensionar os blocos sobre estacas, o programa considera todas as combinações presentes na envoltória para fundações (ELU2).

A partir destes esforços, o programa calcula as forças normais sobre as estacas, utilizando a fórmula abaixo:

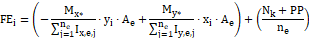
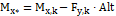
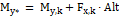
Onde:

.

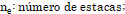
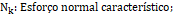
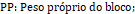
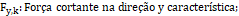
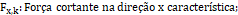
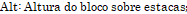
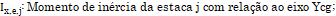
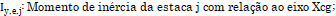
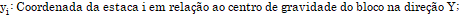
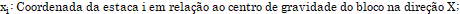
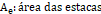No relatório de dimensionamento, o programa irá apresentar três informações importantes para o engenheiro estrutural:

Fmn: Força normal característica mínima observada na(s) estaca(s);

Fmx: Força normal característica máxima observada na(s) estaca(s);

FEq: Força normal característica máxima observada na(s) estaca(s) multiplicada pelo número de estacas.

Estimativa de altura útil

A altura útil, que é usada para o dimensionamento de blocos, pode ser estimada como um fator ou como subtraendo.

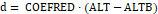
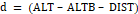
Onde:

d: Altura útil do bloco;

COEFRED: Coeficiente de redução;

ALT: Altura total do bloco;

ALTB: Altura de entrada da estaca no bloco;

DIST: Distância do topo da estaca até o centro de gravidade da armadura de tração.

Para blocos de 7 a 24 estacas, pelo método CEB-FIP, a altura útil é obtida pela expressão (a - b - c - 1,25 cm), onde:

a = altura do bloco;

b = extensão da entrada da estaca no bloco;

c = cobrimento definido.

Este valor será adotado para todos os blocos sobre estacas e, dependendo do valor adotado, o resultado do dimensionamento pode estar contra a segurança.

Consideração sobre a forma do pilar

Para calcular o ângulo da biela de compressão e a armadura principal do bloco sobre estacas, deve-se calcular a distância do pilar ao centro das estacas.

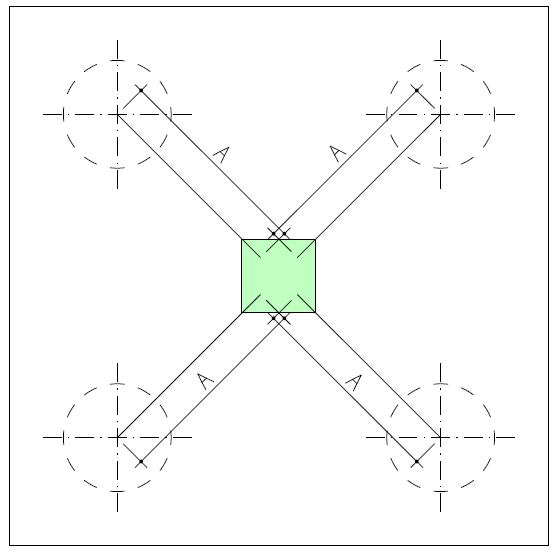
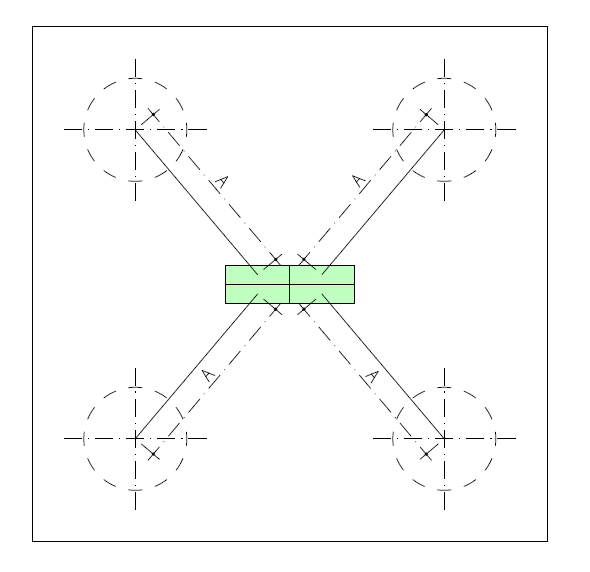
Para blocos de duas estacas e blocos retangulares de 4 a 24 estacas, é possível alterar a maneira que o programa considera a seção transversal do pilar.

Ao realizar esta mudança, o programa irá alterar a maneira de calcular a distância do pilar ao centro das estacas e, consequentemente, irá alterar a fôrma de calcular a inclinação da biela de compressão e a armadura principal dos blocos.

Para estes blocos, o programa apresenta as seguintes maneiras de considerar à seção transversal do pilar:

Quadrado equivalente

Retangular

Nenhuma

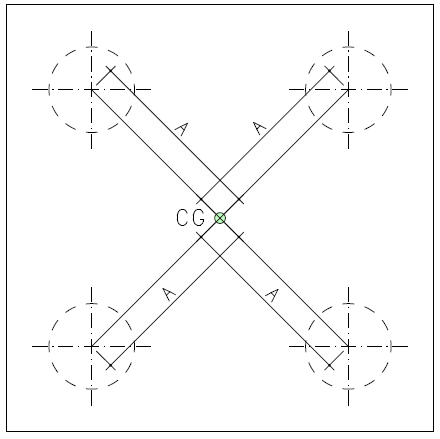
No caso dos blocos de três estacas triangular, cinco estacas pentagonal, cinco estacas disposição 2-3 e seis estacas hexagonal, é possível considerar a seção transversal do pilar como um quadrado equivalente ou a opção nenhuma.

Método de Blèvot

Para bloco de duas estacas, admite-se como modelo resistente, no interior dos blocos de concreto, a treliça indicada abaixo onde barras comprimidas são resistidas pelo concreto e as barras tracionadas pela armadura de aço:

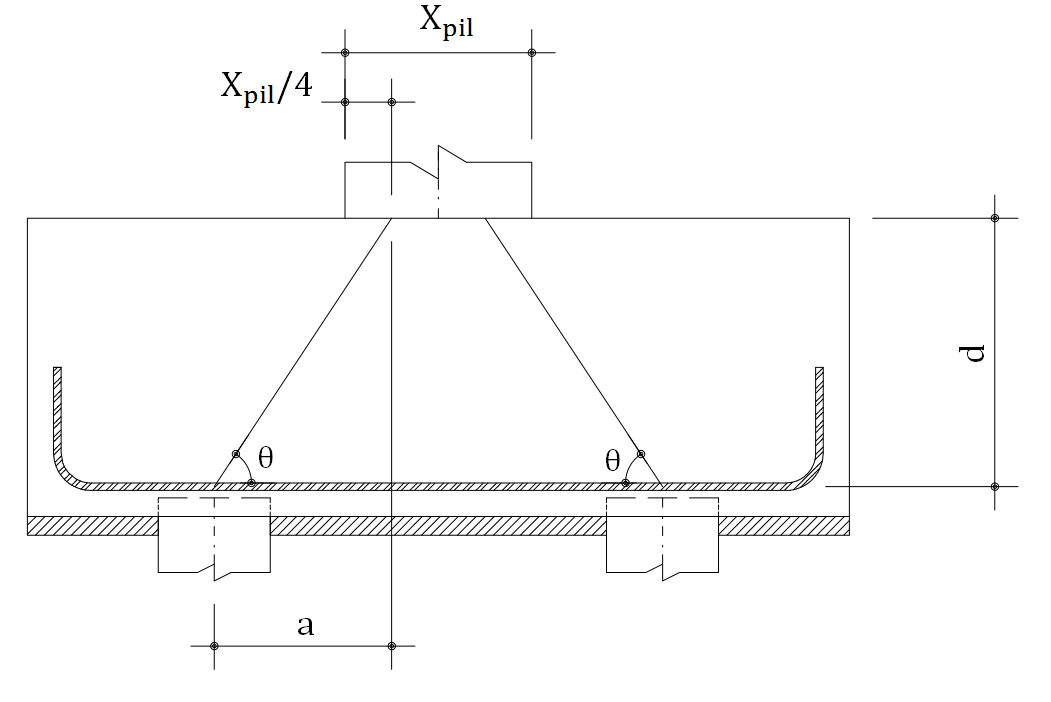
De acordo com método, para o bloco ser rígido, o ângulo de inclinação da biela comprimida deve ser superior a 45°.

Para calcular a tensão biela pilar* (0.1), a tensão biela estaca (0.2), a tensão limite biela pilar (0.3) e a tensão limite biela estaca (0.3), utilizam-se as fórmulas indicadas abaixo:

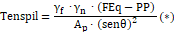	(0.1)
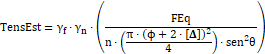	(0.2)
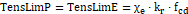	(0.3)

*Obs.: A tensão biela pilar é calculada conforme a fórmula indicada acima ou conforme a fórmula indicada no capítulo 3.9 que muda de acordo com a quantidade e disposição de estacas.

Onde:

Coeficiente ponderador das ações;

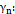Coeficiente adicional ponderador das ações;

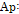Área do pilar;

FEq: Força normal característica máxima observada na(s) estaca(s) multiplicada pelo número de estacas;

PP: peso próprio do bloco sobre estacas;

Ângulo da biela de compressão.

Número de estacas;

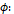Diâmetro das estacas.

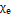: Majorador da tensão admissível;

Coeficiente do efeito Rusch;

Resistência de cálculo do concreto;

A armadura principal é calculada conforme a figura abaixo mostra:

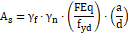
Onde:

Coeficiente ponderador das ações;

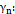Coeficiente adicional ponderador das ações;

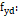Resistência de cálculo do aço;

d: altura útil;

A: Distância do centro das estacas ao pilar. Esta distância varia de acordo com a quantidade de estacas no bloco.

Método A (Fusco, 1994)

Para bloco de duas estacas, utiliza-se um modelo de treliça para dimensionar armaduras e outro modelo para verificar as tensões na área ampliada, a tensão biela pilar e a tensão biela estaca.

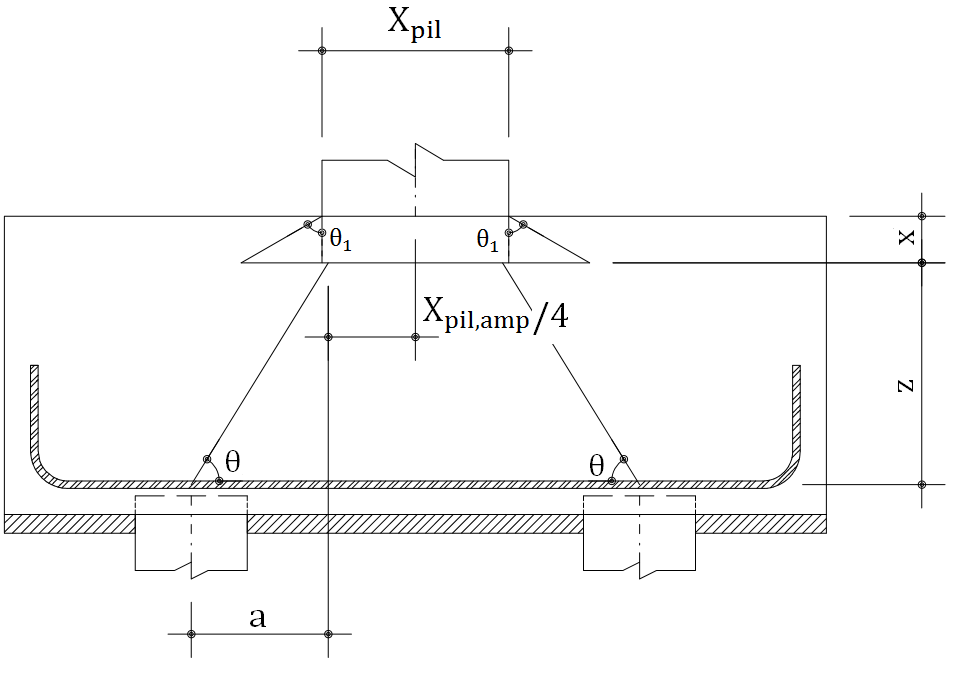
A partir das equações das páginas 344 a 346 de (Fusco, 1994), concluímos que a profundidade x é igual:

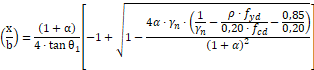
Onde:

b: Representa a menor dimensão do pilar;

α: Representa a relação entre a maior dimensão do pilar e a menor dimensão do pilar;

ρ: Representa a taxa de armadura do arranque;

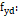Representa a resistência de cálculo da armadura do arranque;

Representa a resistência de cálculo do concreto utilizado no bloco sobre estacas;

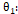Representa o ângulo de espraiamento das tensões;

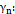Coeficiente adicional ponderador das ações;

A profundidade x é limitada por:

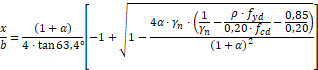	(1)
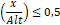	(2)

Onde:

b: Representa a menor dimensão do pilar;

α: Representa a relação entre a maior dimensão do pilar e a menor dimensão do pilar;

ρ: Representa a taxa de armadura do arranque;

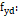Representa a resistência de cálculo da armadura do arranque;

Representa a resistência de cálculo do concreto utilizado no bloco sobre estacas.

Alt: Altura do bloco sobre estacas;

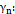Coeficiente adicional ponderador das ações;

De acordo com método, o ângulo de inclinação da biela comprimida deve ser superior a 34°.

Para calcular a tensão na área ampliada (3.6.4), a tensão biela pilar (3.6.5), a tensão biela estaca (3.6.6), a tensão limite na área ampliada (3.6.7), a tensão limite biela pilar (3.6.8) e a tensão limite biela estaca (3.6.9), utilizam-se as fórmulas indicadas abaixo:

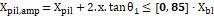	(3.6.1)
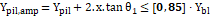	(3.6.2)
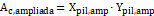	(3.6.3)
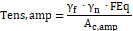	(3.6.4)
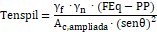	(3.6.5)
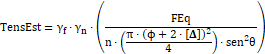	(3.6.6)
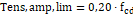	(3.6.7)
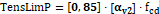	(3.6.8)
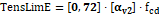	(3.6.9)

Onde:

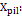Dimensão X do pilar;

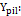Dimensão Y do pilar;

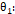Representa o ângulo de espraiamento das tensões;

x: profundidade de espraiamento das tensões;

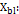Dimensão X do bloco;

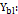Dimensão Y do bloco;

[0,85]: Critério de dimensão da área ampliada;

Coeficiente ponderador das ações;

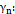Coeficiente adicional ponderador das ações;

FEq: Força normal característica máxima observada na(s) estaca(s) multiplicada pelo número de estacas;

PP: peso próprio do bloco sobre estacas;

Ângulo da biela de compressão.

Número de estacas;

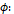Diâmetro das estacas;

Delta para considerar na área ampliada da estacam em cm;

Resistência de cálculo do concreto.

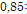Critério multiplicador para resistência da biela junto ao pilar;

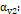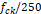(1-), com 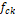em megapascal;

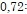Critério multiplicador para resistência da biela junto à estaca;

Para dimensionar as armaduras, utiliza-se o modelo indicado abaixo:

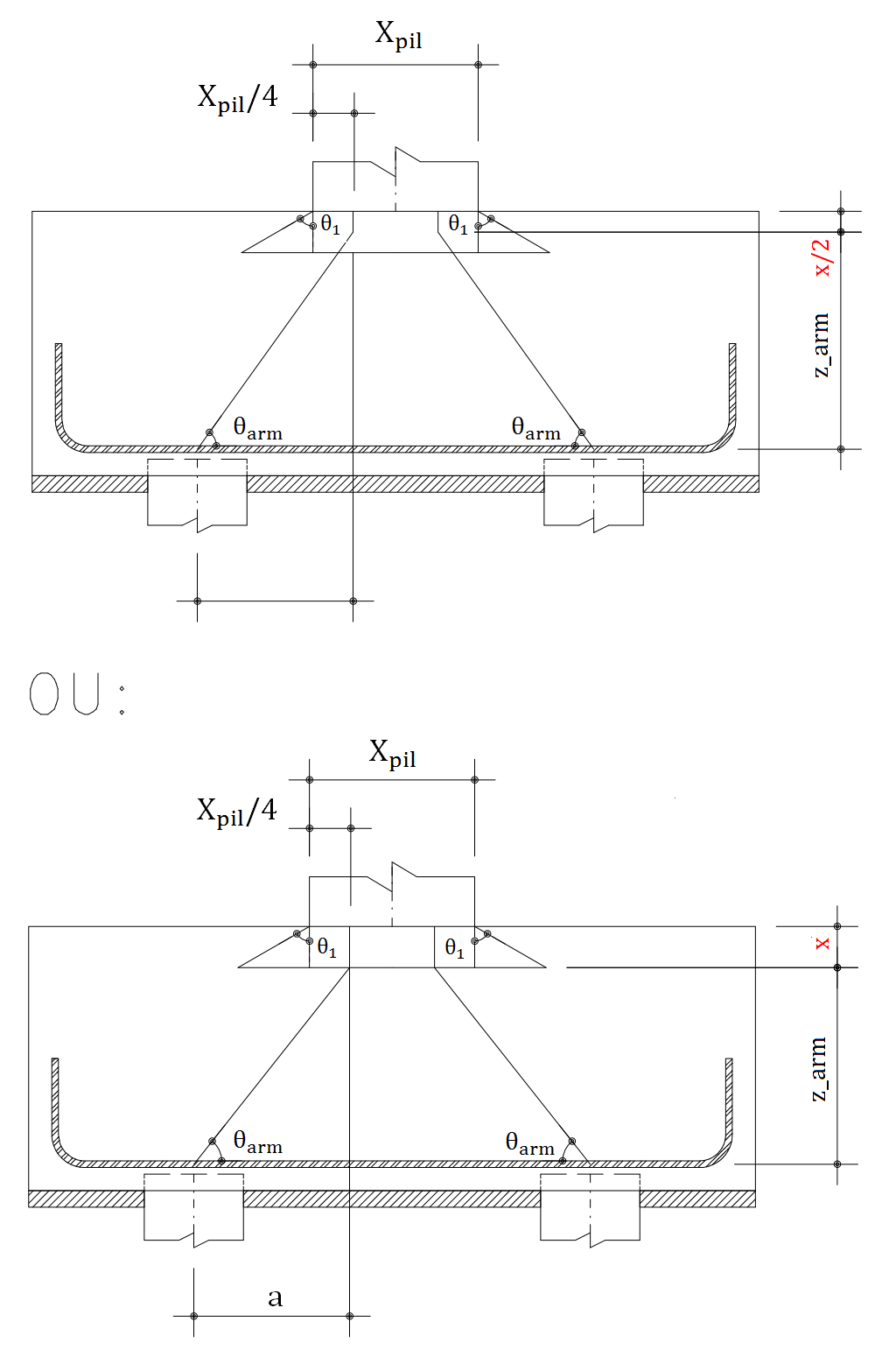
A armadura principal é calculada conforme a figura abaixo mostra:

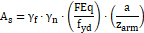
Onde:

Coeficiente ponderador das ações;

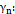Coeficiente adicional ponderador das ações;

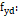Resistência de cálculo do aço;

d: altura útil;

A: Distância do centro das estacas ao pilar. Esta distância varia de acordo com a quantidade de estacas no bloco.

Método B (Fusco, 1994)

Para bloco de duas estacas, utiliza-se um modelo de treliça para dimensionar armaduras e outro modelo para verificar a tensão biela pilar e a tensão biela estaca.

Neste método, estima-se que a profundidade x é o local onde a tensão na área ampliada é igual 20% da resistência do concreto.

Tendo em vista esta premissa, calcula-se a profundidade x, utilizando a fórmula abaixo:

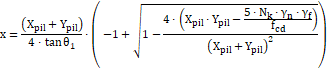
Onde:

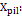Dimensão X do pilar;

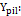Dimensão Y do pilar;

Resistência de cálculo do concreto;

Coeficiente ponderador das ações;

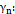Coeficiente adicional ponderador das ações;

Esforço normal característico;

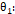Ângulo de espraiamento das tensões sob o pilar.

A profundidade x é limitada por:

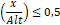
Onde:

Alt: Altura do bloco sobre estacas.

De acordo com método, o ângulo de inclinação da biela comprimida deve ser superior a 34°.

Para calcular a tensão biela pilar (3.7.4), a tensão biela estaca (3.7.5), a tensão limite biela pilar (3.7.6) e a tensão limite biela (3.7.7) estaca, utilizam-se as fórmulas indicadas abaixo:

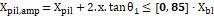	(3.7.1)
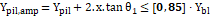	(3.7.2)
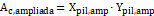	(3.7.3)
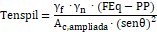	(3.7.4)
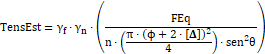	(3.7.5)
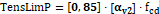	(3.7.6)
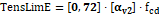	(3.7.7)

Onde:

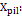Dimensão X do pilar;

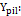Dimensão Y do pilar;

x: Profundidade do espraiamento de tensões;

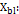Dimensão X do bloco;

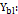Dimensão Y do bloco;

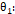Ângulo de espraiamento das tensões sob o pilar;

[0,85]: Critério de dimensão da área ampliada;

Coeficiente ponderador das ações;

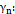Coeficiente adicional ponderador das ações;

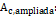Área ampliada;

FEq: Força normal característica máxima observada na(s) estaca(s) multiplicada pelo número de estacas;

PP: peso próprio do bloco sobre estacas;

Ângulo da biela de compressão.

Número de estacas;

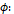Diâmetro das estacas;

Delta para considerar na área ampliada da estacam em cm;

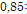Critério multiplicador para resistência da biela junto ao pilar;

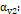(1-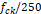), com 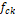em megapascal;

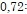Critério multiplicador para resistência da biela junto à estaca;

Para dimensionar as armaduras, utiliza-se o modelo indicado abaixo:

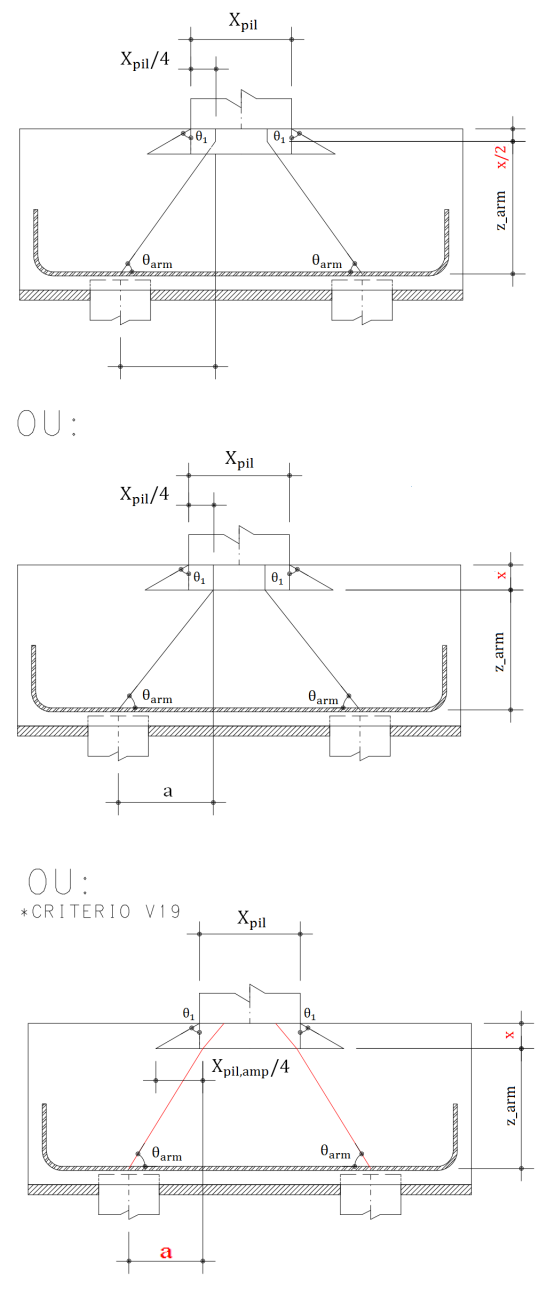
A armadura principal é calculada conforme a figura abaixo mostra:

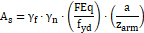
Onde:

Coeficiente ponderador das ações;

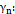Coeficiente adicional ponderador das ações;

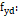Resistência de cálculo do aço;

d: altura útil;

A: Distância do centro das estacas ao pilar. Esta distância varia de acordo com a quantidade de estacas no bloco.

MBT

O MBT ou Método de Bielas e Tirantes é baseado nos Comentários do Ibracon (ABNT NBR 6118:2014 Comentários e exemplos de aplicação, 2015).

Para bloco de duas estacas, admite-se como modelo resistente, no interior dos blocos de concreto, a treliça indicada abaixo onde barras comprimidas são resistidas pelo concreto e as barras tracionadas pela armadura de aço:

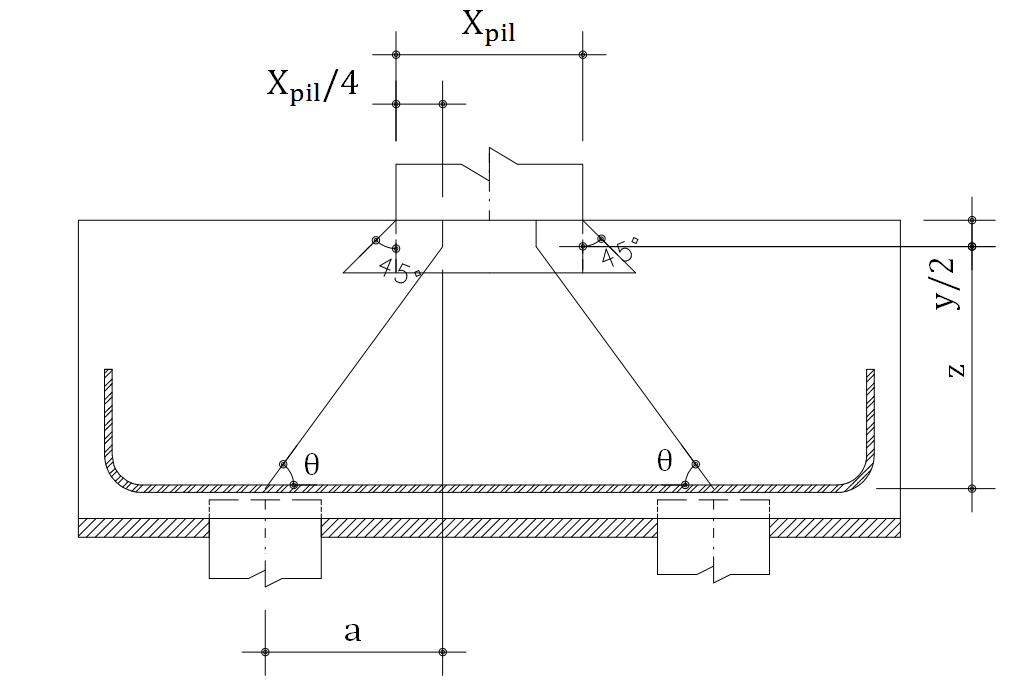
A profundidade y consiste no ponto onde a tensão biela pilar é igual à tensão biela pilar limite, considerando um ângulo de espraiamento de tensões sob o pilar a 45°.

A profundidade y é limitada por:

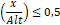
Onde:

Alt: Altura do bloco sobre estacas.

De acordo com método, o ângulo de inclinação da biela comprimida deve ser superior a 34°.

Para calcular a tensão biela pilar (3.8.4), a tensão biela estaca (3.8.5), a tensão limite biela pilar (3.8.6) e a tensão limite biela (3.8.7) estaca, utilizam-se as fórmulas indicadas abaixo:

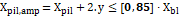	(3.8.1)
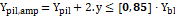	(3.8.2)
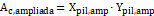	(3.8.3)
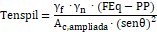	(3.8.4)
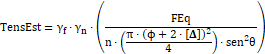	(3.8.5)
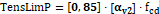	(3.8.6)
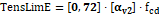	(3.8.7)

Onde:

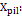Dimensão X do pilar;

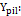Dimensão Y do pilar;

x: Profundidade do espraiamento de tensões;

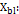Dimensão X do bloco;

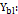Dimensão Y do bloco;

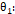Ângulo de espraiamento das tensões sob o pilar;

[0,85]: Critério de dimensão da área ampliada;

Coeficiente ponderador das ações;

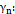Coeficiente adicional ponderador das ações;

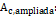Área ampliada;

FEq: Força normal característica máxima observada na(s) estaca(s) multiplicada pelo número de estacas;

PP: peso próprio do bloco sobre estacas;

Ângulo da biela de compressão.

Número de estacas;

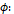Diâmetro das estacas;

Delta para considerar na área ampliada da estacam em cm;

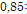Critério multiplicador para resistência da biela junto ao pilar;

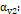(1-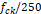), com 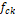em megapascal;

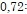Critério multiplicador para resistência da biela junto à estaca;

A armadura principal é calculada conforme a figura abaixo mostra:

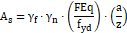
Onde:

Coeficiente ponderador das ações;

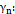Coeficiente adicional ponderador das ações;

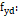Resistência de cálculo do aço;

d: altura útil;

A: Distância do centro das estacas ao pilar. Esta distância varia de acordo com a quantidade de estacas no bloco.