Esforços - Ações Verticais
Este item não é aplicável ao modelo estrutural “IV Modelo integrado e flexibilizado (conforme critério) de pórtico espacial”. Os modelos estruturais são definidos no Editor de Edifício.
Trataremos, neste item, dos seguintes tópicos relativos as cargas verticais (peso próprio + cargas variáveis) quando o modelo adotado não for o de pórtico espacial:
- Cargas verticais centradas
- Cargas verticais excêntricas devido ao:
- Cálculo de vigas + pilares
- Excentricidade geométrica do pilar
- Excentricidade geométrica do ponto de aplicação das cargas
- Consideração de momentos externos
- Distribuição de momentos fletores nos pilares
A determinação dos esforços solicitantes nos pilares devido a cargas verticais é bastante polêmica. Se por um lado, todo projetista tem a maior facilidade em determinar a força vertical atuante no pilar, por outro, aparecem inúmeras dúvidas sobre os momentos fletores que atuam nos pilares devido a presença desta carga vertical.
Modelo da viga contínua considerando pilares
Tudo se inicia no cálculo da simples viga contínua, engastada nos pilares superiores e inferiores como no exemplo abaixo (não é aplicável quando adotado o modelo “IV Modelo integrado e flexibilizado (conforme critério) de pórtico espacial”, no editor de edifício, pois as solicitaçõs devido às cargas verticais são provenientes do cálculo do pórtico espacial ELU):
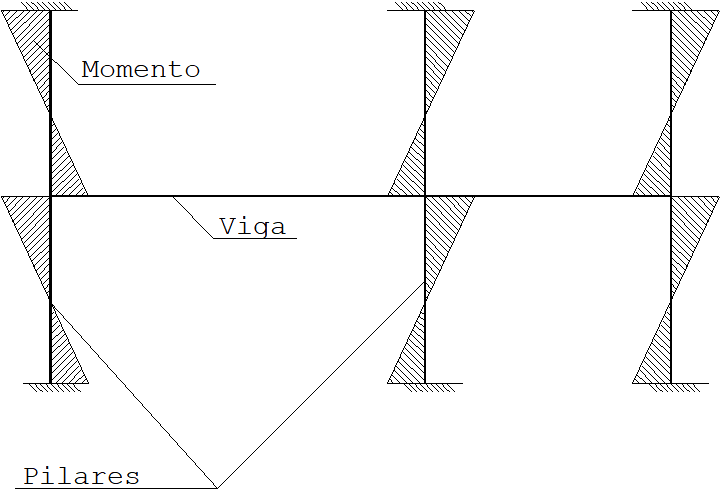
A resolução do modelo acima fornece, nos pilares inferiores e superiores, momentos fletores devido a cargas verticais. Estas solicitações estão presentes nos pilares extremos e também nos pilares internos.
Estas solicitações devem ou não ser consideradas? O TQS Pilar pode ou não considerá-las, dependendo do critério de projeto adotado pelo usuário. Sob o ponto de vista teórico, este é um modelo adequado pois não se pode esquecer, do ponto de vista da Resistência dos Materiais, da presença dos pilares superiores e inferiores.
Nota: A viga contínua com os apoios tratados como articulados e resistentes a apenas cargas verticais não vai introduzir momentos fletores nos pilares. Este é um modelo utilizado durante décadas por centenas de projetistas de concreto armado em todo o Brasil.
Excentricidades geométricas
Quando um pilar muda de seção transversal de um pavimento ao outro, pode ocorrer a existência de uma excentricidade entre os baricentros nos dois lances contíguos como é apresentado no desenho abaixo:
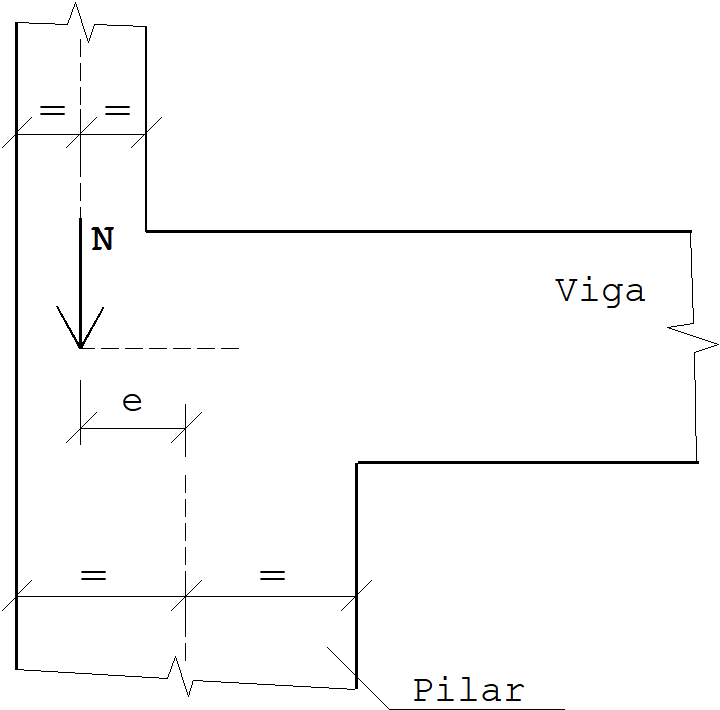
É evidente que esta excentricidade provocará um momento fletor nos pilares e nas vigas adjacentes. Estes momentos devem ser considerados ou não? Valem as mesmas observações apresentadas acima no caso de viga contínua.
Outro caso interessante é a introdução das cargas verticais das vigas, nos pilares de dimensões elevadas. É muito comum, nas atuais edificações, que estes pilares recebam cargas concentradas de vigas nas extremidades como a figura apresenta abaixo:
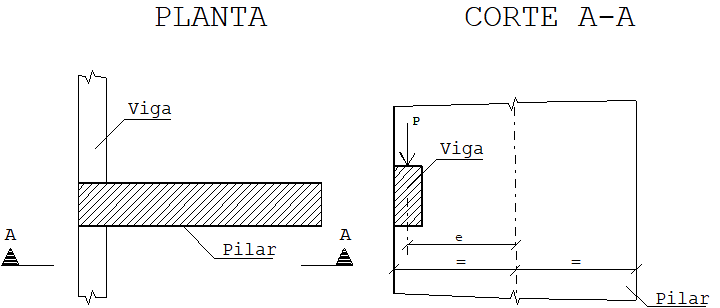
Estas cargas, quando transportadas para o baricentro dos pilares, provocam também momentos fletores elevados que não podem ser desprezados. Como considerar adequadamente estes momentos nos diversos pilares? Esta é uma tarefa para os diversos critérios de projeto do TQS Pilar de tal forma que, se possa conciliar as normas de projetos distintas de diversos usuários e que abordaremos no item abaixo.
Vale aqui uma importante observação: diversos projetistas com grande experiência profissional, e com centenas de obras de grande porte projetadas, salvo algumas exceções, praticamente desprezam estes momentos fletores nos pilares devido a cargas verticais. A alegação é a de que o efeito conjunto dos elementos de vigas + pilares + lajes, todos solidários e trabalhando em conjunto, minimizam os efeitos destes momentos fletores que podem ser praticamente desprezados. Esta é uma posição que pode ser adotada por profissionais de extrema experiência. Há algumas décadas passadas, não existiam ferramentas computacionais adequadas para tratamento destes problemas e, por esta razão, soluções simplificadoras mas, seguras, eram adotadas baseadas na experiência profissional.
Atualmente com os recursos computacionais oferecidos, recomenda-se que estes efeitos sejam analisados convenientemente e, quando for o caso, podem ser desprezados. Apresentaremos a seguir uma alternativa existente no TQS Pilar para tratamento destes momentos fletores de forma um pouco mais adequada. A solução final aconselhada e, tecnicamente correta nestes casos, é a análise da edificação pelo modelo de pórtico espacial para cargas verticais. Este recurso, que até pouco tempo atrás era extremamente trabalhoso, pode ser agora ser tratado de forma simples e prática pelo sistema TQS Formas - opção Pórtico Espacial.
Consideração dos momentos externos
A simples acumulação dos momentos fletores, devido a excentricidade geométrica da seção transversal e do ponto de aplicação das cargas, ao longo de todos os lances da edificação, geralmente resulta em superdimensionamento das armaduras pois estes momentos na prática se redistribuem ao longo dos diversos lances.
Neste item, trataremos como esta distribuição de momentos pode ser realizada pelo TQS Pilar.
Acumulam-se os momentos externos
Pilares rígidos que acumulam os momentos fletores ao longo da edificação, isto é, pilares que se deslocam na direção horizontal com a absorção destes momentos fletores.
Pilares flexíveis que redistribuem os momentos fletores no próprio pavimento e no lance imediatamente superior e inferior do lance em estudo, isto é, pilares que giram, sem deslocamento horizontal e que não absorvem estes momentos fletores na sua integridade.
Esquematicamente podemos mostrar como esta propagação de momentos é realizada ao longo dos lances do pilar.
- Acumulo de momentos:
| Momentos aplicados | Momentos calculados | |||
| nos pisos i, i-1 e i-2 | nos pisos i, i-1 e i-2 | |||
| Me i | Mc i,i | Mc i,s | ||
| Me i-1 | Mc i-1,i | Mc i-1,s | ||
| Me i-2 | Mc i-2,i | Mc i-2,s | ||
Temos:
- Para o lance i:
Mc i,i= Me i
Mc i,s= Me i
- Para o lance i-1:
Mc i-1,i= Me i + Me i-1
Mc i-1,s= Me i + Me i-1
- Para o lance i-2:
Mc i-2,i= Me i + Me i-1 + Me i-2
Mc i-2,s= Me i + Me i-1 + Me i-2
Este cálculo é realizado para todos os pilares/lances da edificação e todos os momentos nos pilares são acumulados. Note que para o pilar deslocável, estes momentos devido às excentricidade são acumulados do topo para a base.
Propagam-se os momentos externos
- Propagação de momentos:
| Momentos aplicados | Momentos calculados | ||||
| nos pisos i, i-1 e i-2 | nos pisos i, i-1 e i-2 | ||||
| Me i | Mc i,i | Mc i,s | |||
| Me i-1 | Mc i-1,i | Mc i-1,s | |||
| Me i-2 | Mc i-2,i | Mc i-2,s | |||
Por hipótese, o pilar é considerado engastado no lance superior e inferior. Assim a propagação dos momentos para o topo do lance superior e base do lance inferior é feita com o coeficiente 0.5.
Sendo:
r i= rigidez do pilar no lance i= I i / L i
r i-1= rigidez do pilar no lance i-1= I i-1 / L i-1
r i-2= rigidez do pilar no lance i-2= I i-2 / L i-2
Temos:
- Para o momento Mei:
- Para o lance i:
M1 t,i=Mei
M1 b,i=Mei 0.5
- Para o lance i-1:
M1 t,i-1=0
M1 b,i-1= 0
- Para o lance i-2:
M1 t,i-2=0
M1 b,i-2=0
- Para o momento Mei-1:
Para o lance i:
M2 t,i=Mei-1
M2 b,i=Mei-1
- Para o lance i-1:
M2 t,i-1=Mei-1
M2 b,i-1=Mei-1
- Para o lance i-2:
M2 t,i-2=0
M2 b,i-2=0
- Para o momento Mei-2:
- Para o lance i:
M3 t,i=0
M3 b,i=0
- Para o lance i-1:
M3 t,i-1=Mei-2
M3 b,i-1=Mei-2
- Para o lance i-2:
M3 t,i-2=Mei-2
M3 b,i-2=Mei-2
- E os momentos finais de cálculo são obtidos:
- Para o lance i:
Mci , s=M1 t,i+M2 t,i+M3 t,i
Mci , i=M1 b,i+M2 b,i+M3 b,i
- Para o lance i-1:
Mci-1 , s=M1 t,i-1+M2 t,i-1+M3 t,i-1
Mci-1 , i=M1 b,i-1+M2 b,i-1+M3 b,i-1
- Para o lance i-2:
Mci-2 , s=M1 t,i-2+M2 t,i-2+M3 t,i-2
Mci-2 , i=M1 b,i-2+M2 b,i-2+M3 b,i-2
Este cálculo é realizado para todos os pilares/lances da edificação e todos os momentos nos pilares são acumulados. Note que para o pilar indeslocável, estes momentos devido às excentricidade não são acumulados do topo para a base.
Acumula/Propaga percentualmente os mom. externos
Na edificação, nem todos os pilares terão os momentos externos acumulados ou propagados. Geralmente o que ocorre é um misto da presença destes pilares. No TQS Pilar, permite-se que o usuário defina o quanto o pilar é flexível e o quanto o pilar é rígido através de uma porcentagem.
Assim, o projetista de posse da planta de formas, analisando criteriosamente a disposição e rigidez dos pilares, vai arbitrar para cada um dos pilares um valor de acumulo e/ou propagação. Com estes valores a parcela dos momentos externos são distribuídos nos pilares conforme as expressões mostradas acima, com todos os seus efeitos combinados. Esta é uma maneira aproximada mas, de boa confiabilidade para não desprezar, simplesmente, estes momentos.
Por exemplo, num edifício convencional onde um pilar "parede" tem grandes dimensões perante os demais e recebe reações de vigas nas suas extremidades, podemos assumir que 90% deste irá trabalhar acumulando os momentos externos e 10% propagando. Neste mesmo exemplo, para os pilares de dimensões reduzidas que não colaborarão na rigidez da edificação, podemos assumir que estes pilares trabalharão como 100% de propagação.
- Sendo:
Me - momento total no nó i.
MeD - momento para o sistema considerado deslocável
MeI - momento para o sistema considerado indeslocável
f - fator para distribuição dos momentos Me (Propagação)
- Temos:
MeD = Me (1 - f)
MeI = Me f
Após esta distribuição, o roteiro para cálculo dos momentos finais seguem os mesmos roteiros apresentados antes, especificamente para cada "sistema" em separado, e depois são somados os momentos em cada extremidade do lance.
Observação importante: Dependendo do critério K10, a apresentação destes resultados poderão diferir quando ao conteúdo. Quando é usado K10=Nao, é tomado o maior dos momentos no lance para efeito de cálculo. Caso contrário, são tomados , na parte de carregamentos, são listados estes valores, bem como no "rodapé" de cada pilar as condições de acumulo ou propagação dos momentos externos do pilar, permitindo ao usuário uma completa visualização da situação.
Note que fazendo f = 0, equivale ao caso de pilar deslocável, e com f = 1, ao do pilar onde os momentos serão acumulados.
Tratamento de cargas verticais pelo TQS Pilar
O TQS Pilar respeita os critérios usuais do usuário e não faz imposição rígida do modo de projetar.
Não cabe ao sistema TQS Pilar, determinar qual o método é o mais correto para esta determinação de solicitações. Cabe ao projetista a seleção do critério que julgar mais adequado ao seu projeto e, acompanhando a técnica usual e consagrada sob o ponto de vista prático e teórico da arte de projetar.
