Esforços - Ações Horizontais
Ao analisar os pilares da edificação, devem ser considerados os efeitos devido a atuação das cargas horizontais, geralmente originários da ação do vento. Para esta análise, o TQS Pilar permite a utilização de diversos processos que são listados abaixo:
- Esforços devido a cargas horizontais - pórtico espacial
- Esforços devido a cargas horizontais - fornecimento direto
- Esforços devido a cargas horizontais - processo simplificado
A não consideração dos efeitos de cargas horizontais deve ser realizada criteriosamente não dispensando, enfatizando mais uma vez, a análise da estabilidade global da edificação.
Esforços proveniente do cálculo de Pórtico Espacial
Este é o modelo mais adequado para a análise dos efeitos de cargas horizontais nos edifícios. As simplificações acima são tratadas corretamente pelo modelo espacial criado. Algumas vantagens na utilização deste modelo:
- As excentricidades devido às variações da seção do pilar são consideradas.
- As excentricidades devido a introdução de cargas excêntricas nos pilares são consideradas.
- Os vãos das vigas são tratados considerando os trechos rígidos pertencentes ao interior dos pilares.
- Os pilares são considerados segundo os eixos centrais de inércia.
- Os efeitos do "giro" do edifício segundo seu eixo vertical é automaticamente computado.
- Os deslocamentos horizontais devido as cargas verticais são tratados.
- Se necessário, as deformações axiais dos pilares podem ser analisadas.
- Pode-se analisar a edificação com a aplicação de cargas horizontais de vento em quaisquer direções.
- Análise dos esforços devido a atuação de outras cargas horizontais como empuxo, protensão, etc.
- Pode-se fazer o processamento de carregamentos independentes e combiná-los para efeitos de obtenção de envoltórias de carregamentos para cargas verticais e horizontais.
Um ponto importante a ressaltar é o controle da transferência dos esforços provenientes de pórtico espacial para o sistema TQS Pilar.
Como a filosofia dos Sistemas TQS é dar a maior flexibilidade possível ao usuário, deixamos por conta do projetista o fornecimento das variáveis que governam esta transferência. Assim, o projetista determina a combinação de carregamentos desejada, quais carregamentos serão transferidos ao TQS Pilar, quais as reduções de cargas horizontais que deverão ser feitas antes da transferência, etc.
Esforços devido a cargas horizontais - Fornecimento direto
As solicitações devido às cargas horizontais podem ser, em último caso, ser fornecidas diretamente pelos usuários no arquivo de dados, em cada lance da edificação. Este é um caso necessário quando a análise das solicitações não for realizada por um dos Sistemas TQS. A grande dificuldade nesta opção é o enorme volume de informações a serem introduzidas pois, para cada lance/pilar/carregamento devem ser fornecidos 3 grandezas no topo e 3 grandezas na base de cada elemento (pilar/lance).
Para uma generalização completa dos casos abrangidos pelo TQS Pilar, esta opção está atualmente presente.
Esforços devido a cargas horizontais - Processo simplificado sem vigas
Este processo se baseia na distribuição de forças normais e momentos fletores de forma proporcional a rigidez dos pilares e sua distância ao baricentro da edificação, sem considerar a rigidez real das diversas vigas que unem os vários pilares (faz-se uma estimativa de que o momento fletor resultante se distribua igualmente para as vigas e os pilares). Este é um cálculo simplificado que deve ser utilizado apenas quando não for possível o acesso a métodos mais exatos.
Neste caso, assume-se como hipótese básica a existência de lajes em cada pavimento, com espessura reduzida e de dimensões tais que elas podem ser consideradas como rígidas nas direções do seu plano, assegurando que os deslocamentos horizontais dos vários pilares sejam os mesmos nas duas direções do plano a menos do movimento de corpo rígido (translação e rotação).
O momento fletor total em cada piso da edificação, é determinado adotando-se a simplificação de tratar o modelo do edifício de forma unifilar reduzido a uma barra em balanço com o eixo passando pelo ponto G (baricentro) do pavimento e calculado em função da distribuição e das seções dos pilares na planta. Cada momento fletor total Mj de um piso j é distribuído proporcionalmente a certas grandezas dos pilares para manter o equilíbrio entre os esforços externos e os esforços internos (força normal e momento fletor) nos diversos pilares.
Cálculo em função do momento de inércia dos pilares
Para melhor ilustrar este cálculo, é assumindo um sistema de coordenadas X', Y' com origem no canto inferior esquerdo da planta dos pilares e paralelos aos eixos X, Y globais.
O sistema U, V passa pelo baricentro dos pilares, ponto G, e é paralelo aos eixos X e Y. A figura abaixo mostra os dois sistemas de referência:
O eixo que passa pelo ponto G, é calculado em função dos momentos de inércia dos pilares como sendo:
Sendo:
Jxi e Jyi - os momentos de inércia do pilar i nas direções x e y respectivamente.
xi e yi - as coordenadas do pilar i no sistema x, y.
Sendo Mxj e Myj os momentos fletores totais na base do lance j no ponto G do piso, os momentos em cada pilar i no lance j são calculados pela expressão:
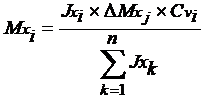
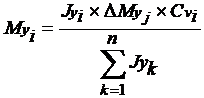
Onde:
Cvi - relação entre a rigidez do pilar e a rigidez das vigas a ele conectados. Adota-se por exemplo o valor 0.5 aproximadamente.
Mxj e Myj - diferenças dos momentos nos pisos consecutivos
(Mxj = Mx - Mx+1, Myj= Myi - Myi+1).
A força normal no lance j do pilar i é dada pela fórmula:
Onde :
Mxj e Myj - momentos totais na base do lance j.
Uj e Vj - coordenadas do pilar i no sistema (U, V), sistema paralelo a (X, Y), passando pelo ponto G.
Neste método, são computados para os pilares os esforços de força normal e momento fletor para cada direção.
Cálculo em função da área dos pilares
O eixo da barra que passa pelo ponto G é calculado em função das áreas dos pilares como sendo:
Onde :
Aj - área do pilar i
xj e yj - coordenadas do pilar i no sistema (X, Y).
Determinam-se os eixos principais de inércia (U, V) no ponto G para o conjunto total de pilares.
Os momentos MUj e MVj no ponto G, na base do lance j, são determinados a partir dos momentos Mxj e Myj.
Determinam-se os esforços normais no pilar i por :
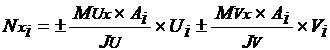
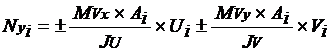
Sendo:
Ju e Jv - momentos principais de inércia do conjunto de pilares.
Uj e Vj - coordenadas dos pilar i no sistema (U, V).
Neste método, são adicionados aos pilares apenas os esforços de força normal para cada direção.
Cálculo em função da carga nos pilares
O eixo da barra passa pelo ponto G, é calculado em função das cargas nos pilares como sendo:
Sendo :
Pti - carga do pavimento em estudo no pilar i
xi e yj - coordenadas do pilar i no sistema (X , Y)
O momento de "inércia" do conjunto em função das cargas dos pilares é dado pela expressão:
Onde :
Ui e Vi - momentos de "inércia" em função da carga em relação aos eixos (U, V), eixos paralelos aos eixos (X, Y) e passando pelo ponto G.
Sendo MUj e MVj, os momentos totais na base do lance j no ponto G do piso, a força normal em cada pilar i é calculada pela fórmula
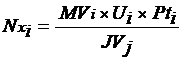
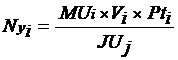
Onde:
Ui e Vi - coordenadas do pilar i no sistema de coordenadas (U, V).
Neste método, são adicionados aos pilares apenas os esforços de força normal para cada direção.
