Flexão Oblíqua

Este é o caso mais comum e seu tratamento no TQS Pilar é o mais genérico possível.

Será feita uma exposição do dimensionamento da seção submetida a flexão composta oblíqua que é o caso geral. O dimensionamento da flexão composta normal é um caso particular da flexão composta oblíqua.

O que será exposto a seguir é o tratamento realizado pelo TQS Pilar tanto para pilares retangulares e pilares de seções genéricas.

Hipóteses adotadas

a) Diagramas tensão - deformação dos materiais

• Concreto

A relação entre tensões e deformações no concreto é representada pelo diagrama abaixo:

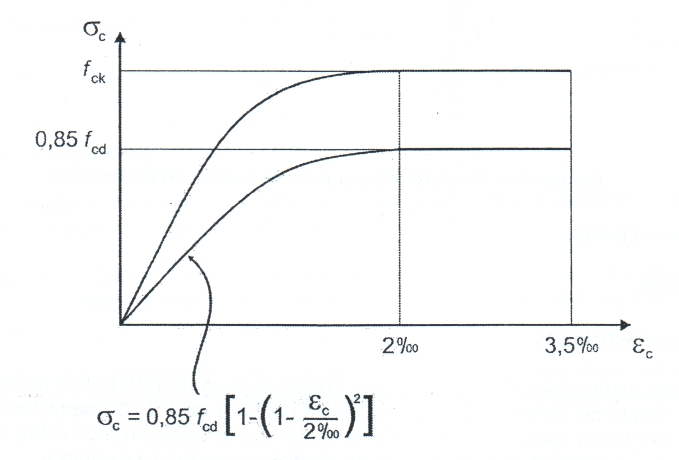
• Aço

Para os aços da classe B, apresentamos, abaixo, o diagrama tensão - deformação com temos o diagrama de

Para os aços da classe B temos o seguinte diagrama tensão - deformação com a simplificação permitida pela NBR-6118 para a curva do aço:

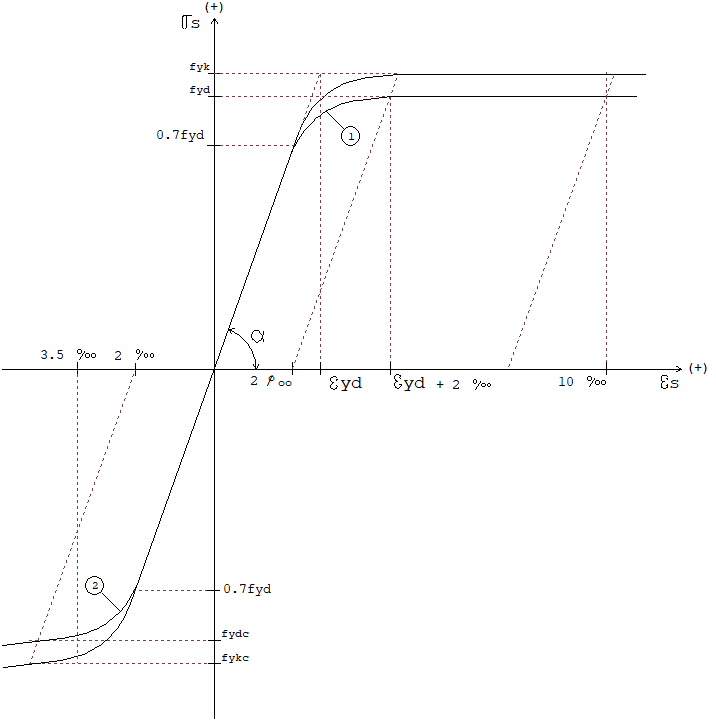
Onde:

= arctg Es

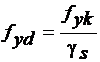
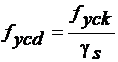
e o trecho é dado pela equação abaixo, conforme item 7.2 da NBR-6118:

com Es = 2.1 106

Para o trecho , a expressão é a mesma acima, mas com o termo fyd substituído por fydc.

Para os aços da classe A temos o seguinte diagrama tensão/deformação :

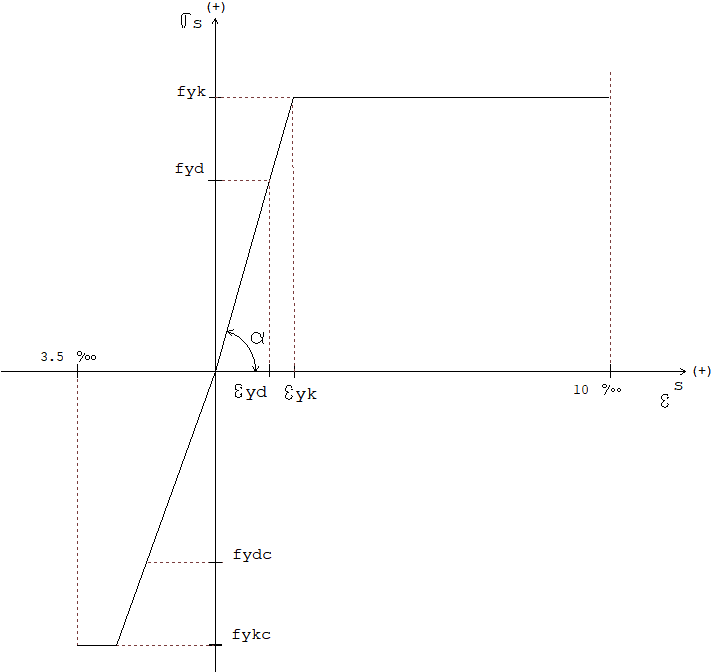
Onde:

= arctg Es

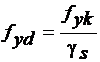
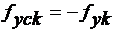
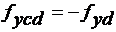
b) Seções planas

Admite-se válida a hipótese das seções planas ou seja, as seções transversais permanecem planas e normais ao eixo da peça após as deformações.

c) Esgotamento da capacidade resistente da seção

A resistência de uma seção transversal é limitada pela ocorrência de uma deformação considerada excessiva na armadura, ou então, um encurtamento relativo no concreto que produza o seu esmagamento. Limita-se o alongamento relativo na armadura em 10 o/oo (zona I). Considera-se que o esmagamento do concreto ocorre quando o seu encurtamento relativo atinge 3.5 o/oo em seções parcialmente comprimidas (zona II), ou (3.5 o/oo - 0.75i) em seções totalmente comprimidas (zona III). O valor i representa o encurtamento na fibra inferior da seção.

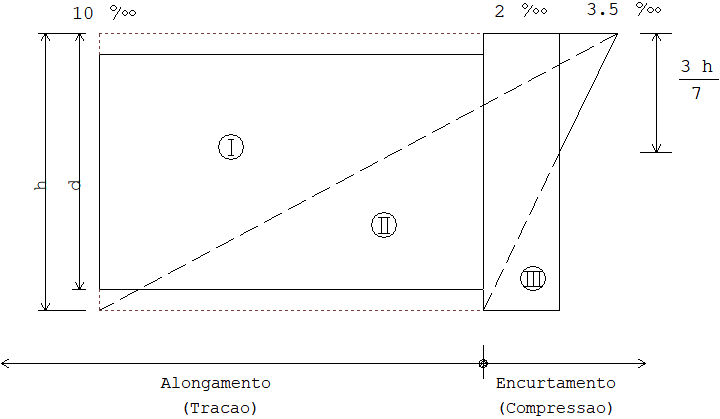
Se o programa computacional não conseguir, em um certo número limitado de iterações, atingir o equilíbrio de esforços externos e internos, obedecendo aos limites acima definidos e, desde que os parâmetros de convergência forem escolhidos convenientemente, concluímos também que a capacidade resistente da seção está esgotada.

d) Carregamentos

Considera-se que as cargas externas (N, Mx e My), são aplicadas no baricentro da seção de concreto e os eixos X e Y são os eixos centrais de inércia da seção.

e) Discretização da seção transversal

Devido ao caráter geral que se pretende dar ao programa, eliminamos a restrição da possibilidade da aplicação do programa somente a determinados tipos de seções com determinados tipos de armaduras, considerando, no tratamento numérico como se as seções fossem constituídas por uma série finita de pontos, para o aço e concreto assim determinados:

- Pequenos retângulos representando o concreto, identificados por um ponto de coordenadas x, y e respectiva área.

- Pequenos círculos representando as barras de aço, identificados por um ponto de coordenadas x, y e a área da barra.

Neste processo de dimensionamento, com a consideração exata da posição das barras da armadura na seção, é importante observar que a exatidão dos resultados leva a resultados muitas vezes não coincidentes com alguns ábacos existentes no mercado.

Devido as hipóteses de armaduras distribuídas dos ábacos, dimensionado uma seção de largura reduzida sem a consideração da posição exata das barras de ferro leva a resultados diferentes do que os obtidos pelo TQS Pilar onde a posição exata da armadura é considerada. Como a posição da barra de ferro considera o cobrimento da armadura, o estribo e o próprio diâmetro da barra, o braço de alavanca entre as armaduras diminui. Com isto, muitos pilares "passam" pelos ábacos mas "não passam" pelo TQS Pilar. Os resultados do TQS Pilar são resultados precisos para o dimensionamento da seção transversal considerando as posições das barras na sua exata localização.

Processo de análise

a) Variáveis do problema - Flexão Composta Oblíqua

O equilíbrio dos esforços externos e internos para as seções transversais submetidas a flexão composta oblíqua é governado por 3 variáveis (duas rotações e uma translação) interdependentes entre si, representadas esquematicamente como abaixo:

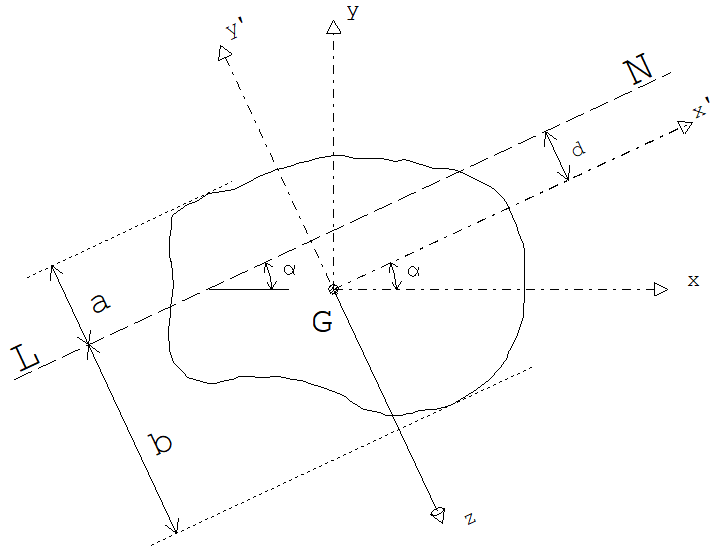
Na figura acima temos:

- O ponto G é o baricentro da seção.

- Os eixos X, Y são os eixos principais de inércia

- O eixo Z forma o sistema de coordenadas X, Y e Z.

Supondo que, nesta seção genérica o equilíbrio entre os esforços internos e externos foi alcançado pela deformação da seção com a linha neutra passando pela reta denominada, na figura, por L N e que a inclinação deste plano deformado com o plano da seção original assume o valor do ângulo temos:

- O ângulo é a inclinação da LN com o eixo x

- O eixo x' passa pelo ponto G formando um ângulo com o eixo x

- O eixo y' é ortogonal ao eixo x' passando por G

- A distância d segundo o eixo y', é a medida entre o ponto G e a linha neutra LN.

Rebatendo a figura no plano y' z temos:

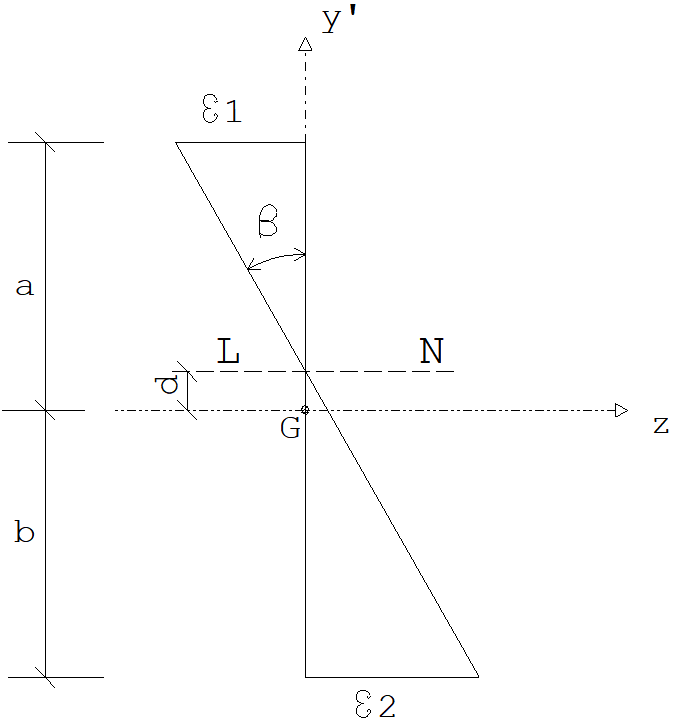
- O ângulo é a inclinação do plano deformado com o plano original da seção.

As três variáveis e incógnitas do problema são:

- Ângulo

- Ângulo

- Distância d

Todo o problema se resume em determinar estas três variáveis de tal forma que os esforços externos sejam equilibrados pelos esforços internos da seção a menos de uma certa tolerância.

b) Esforços resistentes na seção.

Como a seção foi discretizada em pontos, com cada ponto representando pequenos retângulos (concreto) e círculos (aço), o problema da determinação dos esforços resistentes na seção, para uma determinada linha neutra, se resume a:

- Determinação da deformação do ponto com relação a LN da seção.

- A partir da deformação do ponto, e do diagrama tensão - deformação do material, determina-se a tensão no ponto.

- Com a tensão acima determinada e da área do elemento, determina-se a força resistente neste ponto.

- Para todos os pontos da seção, representando a aço e concreto, faz-se a integração abaixo para a obtenção dos esforços finais resistentes.

A figura abaixo ilustra as variáveis de integração:

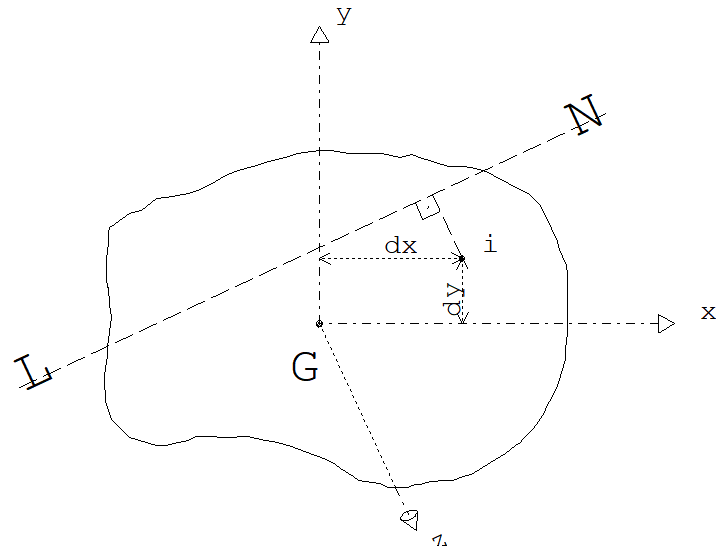
A força normal resistente é calculada como:

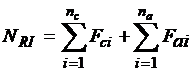
Sendo

Nc = nº de pontos dos retângulos do concreto

Ns = nº de pontos correspondente ao número das barras de aço

Fci = força no ponto i do concreto

Fai = força no ponto i da barra de aço

Nri = resultante da força normal interna na seção.

Os momentos fletores resistentes são calculados como:

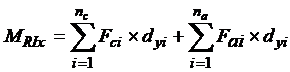
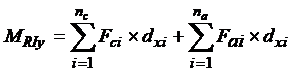
Onde:

dxi= distância do ponto i considerado ao eixo x

dyi= distância do ponto i considerado ao eixo y

MRIx= momento fletor resistente interno no eixo x

MRIx= momento fletor resistente interno no eixo y

c) Processo de convergência

Como as variáveis que estão envolvidas no problema não são lineares, o processo de convergência é iterativo. Todo o problema se resume à resolução de um sistema de 3 equações a 3 incógnitas para cada iteração. Cada solução do sistema de equações induz a uma aproximação da solução desejada.

Assumindo que a profundidade da linha neutra (d) afeta principalmente a força normal, a rotação afeta principalmente o momento em torno do eixo x e a rotação afeta principalmente o momento fletor em torno do eixo y podemos montar o sistema das 3 equações como o representado abaixo:

a11d + a12 + a13 = N

a21d + a22 + a23 = Mx

a31d + a32 + a33 = My

Para a obtenção dos coeficientes aij, basta aplicar a cada uma das três variáveis que governam o problema (d, e ), uma variação unitária e calcular as diferenças (como se fossem as derivadas) dos valores dos esforços internos. Estas variações já são os próprios coeficientes.

O roteiro para encontrar a solução desejada pode ser descrito como sendo:

1)Escolhe-se o ponto de partida das variáveis que podem ser os valores zerados (LN coincidindo com eixo principal e seção sem giro ).

2)Aplicam-se variações unitárias a d, e e encontram-se os valores para aij.

3)Resolve-se o sistema das 3 equações com a primeira aproximação para d, e .

4)Verifica-se se para os valores encontrados de d, e , os esforços internos coincidem com os externos a menos de uma tolerância.

5)Adota-se como origem a nova posição encontrada de d, e .

6)Aplica-se variações unitárias a d, e e encontram-se novos valores para aij.

7)Resolve-se o sistema das três equações com nova aproximação para d, e .

8)Verifica-se se para os valores encontrados de d, e , os esforços internos coincidem com os externos a menos da tolerância.

9)Repete-se o ciclo de operações do item 5) ao 8) até que a solução final seja encontrada.

Ao final do processo de convergência podemos ter 2 situações:

- A solução foi encontrada dentro das tolerâncias e do número de iterações estabelecidos. Este é o caso em que a seção, a priori, "passa".

- A solução não foi encontrada dentro das tolerâncias e do número de iterações estabelecidos. Este é o caso em que a seção "não passa".

d) Verificação final

Obtida a solução para as variáveis d, e , de tal forma que os esforços externos coincidam com os internos, calculam-se as deformações extremas da seção transversal.

Uma última verificação final deve ser realizada para a validade das deformações extremas conforme as deformações admissíveis para os materiais aço e concreto.