Análise Comparativa do Dimensionamento de Pilares entre as Normas NBR 6118:1980 e NBR 6118:2003
1.) Considerações Iniciais
Este artigo tem o objetivo principal de apresentar e comparar os resultados das quantidades de armaduras dos pilares de concreto armado, para um edifício medianamente elevado, segundo as prescrições da nova NBR 6118: 2003. Ele não tem como objetivo a apresentação da parte teórica do cálculo de pilares, o que já é realizado resumidamente no próprio texto da nova Norma e por outras publicações acadêmicas. Para um melhor entendimento deste artigo, o leitor deve estar familiarizado com as novas recomendações para o projeto de pilares, itens 15 e 18 da nova Norma. Assim, citaremos freqüentemente os conceitos de pilar parede, efeito localizado, momento mínimo, efeitos locais de 2ª ordem por curvatura aproximada, kappa aproximado, kappa acoplado a diagrama M-N-1/r etc.
Os resultados apresentados abaixo podem ser extrapolados para outros projetos de edifícios medianamente elevados onde alguns pilares parede estão, necessariamente, presentes para a resistência das forças horizontais de vento.
1.1.) Dados Gerais do Projeto
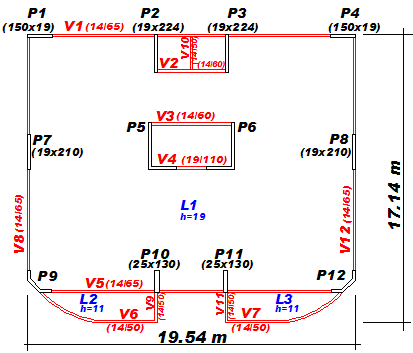
O Edifício Cotoxó, base para o estudo aqui apresentado, é um edifício singular. Ele é o edifício exemplo padrão dos cursos ministrados pelo engenheiro Luiz Aurélio da TQS e conhecido por quase todos os freqüentadores dos cursos. Principais características:
- Edifício residencial em concreto armado com 27 pavimentos.
- Altura total da edificação: 78 m
- Piso a piso médio de 3 m
- Cargas consideradas:
- Verticais: peso próprio, permanentes, alvenarias e variáveis (q = 0.15 tf/m2)
- Horizontais: vento (veloc. básica: 38 m/s, coef. arrasto = 1.2)
- Cobrimento das armaduras: 2.5 cm
- fck dos pilares: até o lance 10: 35 MPa, a partir do lance 11: 30 MPa.
- Vãos médios: 7,0 m
- Resistência ao vento: pórticos e pilares parede.
- Pavimentos com lajes convencionais, lisas e nervuradas.
- Dois pilares sofrem uma transição do pavimento térreo.
- Número total de pilares: 12; outros 12 pilares são apenas "pilaretes" complementares.
- Característica principal dos pilares: praticamente todos os pilares são pilares-parede (dimensão maior > X dimensão menor)
- É um edifício típico residencial esbelto, de altura mediana.
- Carregamentos de vento: 4 (sentido +X, -X, +Y e –Y)
- Número total de carregamentos, apenas para o dimensionamento dos pilares, gerados automaticamente pelo sistema após todas as combinações possíveis: 26
- Nenhum pilar/lance possui índice de esbeltez (λ) acima de 90.
1.2.) Hipóteses Adotadas
Critérios de projeto da NBR 6118:2003
- Adoção do M1d,min para efeitos de imperfeições geométricas locais;
- Dimensão do comprimento equivalente para efeitos de 2ª ordem: Distância piso a piso;
- Efeitos de segunda ordem em que M1ª ordem > M1d,min: proposta do engº Francisco P. Graziano apresentada no ENECE/2004;
- Análise de pilares parede conforme item 15.9 da NBR 6118:2003;
- Demais procedimentos obedecendo a NBR 6118:2003
Critérios de projeto da NBR 6118:1980
- Imperfeição geométrica local através da excentricidade acidental de 2 cm ou h/30;
- Dimensão do comprimento equivalente para efeitos de 2ª ordem: Distância piso a piso;
- Pilares parede com o tratamento convencional;
- Armadura mínima longitudinal de pilar parede de 0.5 %;
- Não adoção dos estribos prescritos (item 6.3.1.4) para pilares parede (50% do As long);
- Deformada dos pilares de seção qualquer como sendo um único plano para a seção transversal;
- Demais procedimentos obedecendo a NBR 6118:1980.
Hipótese básica: Solicitações idênticas para o dimensionamento pelas duas normas.
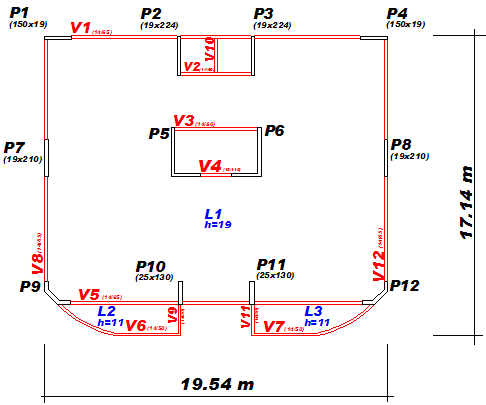
1.3.) Planta e Elevação do Edifício
A seguir, apresentamos a planta do pavimento tipo e algumas vistas 3D da edificação em estudo. Observem na planta abaixo que temos 8 pilares parede retangulares e quatro pilares parede de seção qualquer composto por lâminas.
Visto que o edifício é simétrico com relação ao eixo vertical, apresentaremos resultados apenas para a região a esquerda.
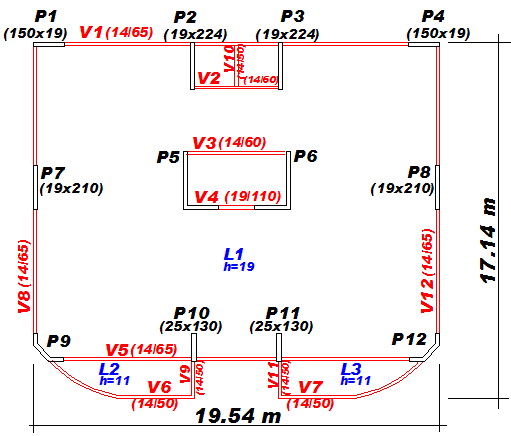
Planta de forma de um dos pavimentos tipo
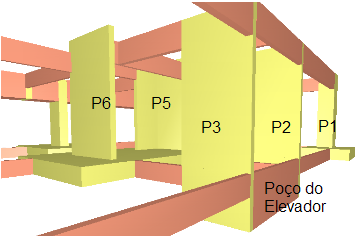
Detalhe do poço do elevador (Lance 1)
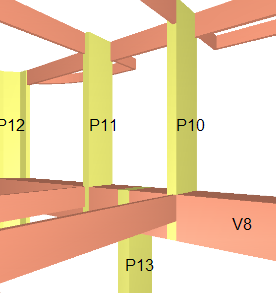
Detalhe dos pilares que nascem na viga de transição (Lance 3)
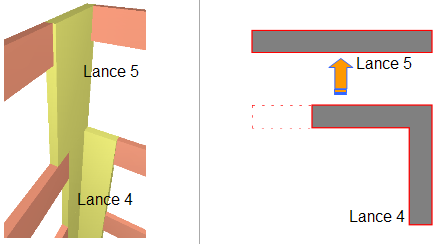
Detalhe do Pilar P4 Lance 4-5 (mudança de seção)
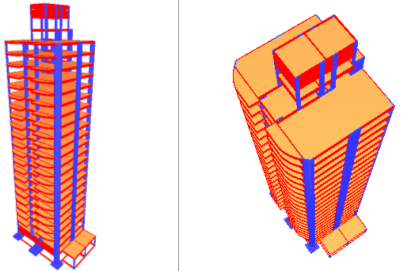
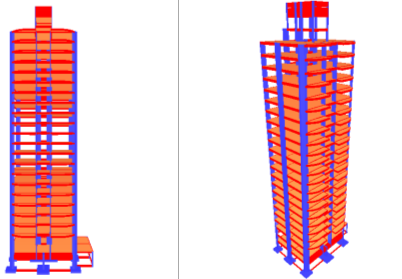
Vistas 3D da edificação
1.4.) Conceito de Pilar Parede
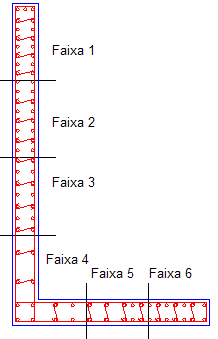
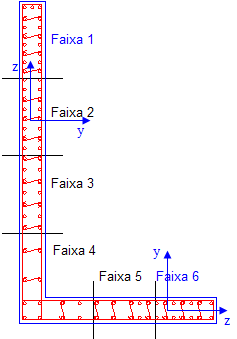
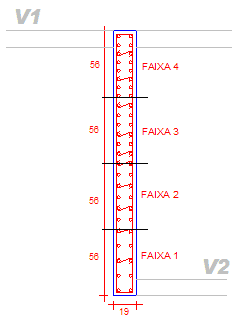
Simplificadamente, a NBR 6118:2003 define como pilar-parede, todo pilar que possui na sua seção transversal, uma dimensão maior que 5 vezes a outra dimensão. Assim, um pilar de 20X100 não é um pilar parede. Já um pilar de 15X80 é um pilar parede. Pilares parede podem ser simples ou compostos. Um pilar retangular é um pilar parede simples. Um pilar em forma de “L”, composto por 2 lâminas, pode ser um pilar parede composto dependendo das dimensões das lâminas. Em função do λ de cada lâmina (35 ≤ λ ≤90), ela deve ser subdivida em faixas e, cada faixa, dimensionada como um pilar independente com os esforços decompostos para cada faixa.
As figuras abaixo ilustram os pilares parede:
| Pilar parede retangular (uma única lâmina) | Pilar parede composto (2 lâminas) |
 |  |
| Pilar parede retangular Lâmina dividida em faixas | Pilar parede composto Lâminas divididas em faixas |
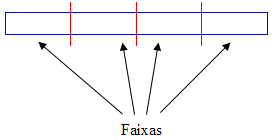 | 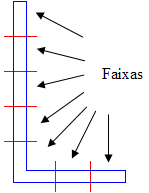 |
2.) Resultados Gerais
Vamos apresentar abaixo resultados globais para todos os pilares do edifício.
2.1.) Resumo Geral de Armaduras
Como já foi afirmado, o processamento levou em consideração as diretrizes da NBR6118: 2003 e, portanto, o correto e completo equacionamento dos pilares parede. Como o detalhamento de estribos em pilares parede foi modificado (25% da área da armadura longitudinal) e obedecido no processamento, salientamos este efeito na tabela abaixo. Vale lembrar que esta consideração era prevista na norma de 1980 como sendo de 50% da armadura longitudinal, a qual, porém, não foi, de forma geral, incorporada pelo mercado.
| NBR 6118: 1980 | NBR 6118 : 2003 | |
| Pilar Parede por Faixas25% Estribo PP | Pilar Parede por FaixasEstribo convencional | |
| 56,1 | 56,8 | 50,7 |
| --- | ( + 1,2 %) | ( - 9,6 %) |
Nota-se que houve um aumento de armaduras com a NBR6118: 2003 na comparação acima. Isto, de certa forma, contradiz as afirmações que vinham sendo feitas até agora com relação às armaduras calculadas pela NBR6118:1980 e NBR6118:2003, neste projeto específico. Oportunamente, explicaremos melhor este acréscimo de armaduras. Vamos analisar as variações, com mais detalhes, para cada pilar.
2.2.) Resumo Geral de Armaduras por Pilar
| PILAR | NBR6118:1980(kg) | NBR6118:2003(kg) | Diferença(kg) | Diferença(%) | NBR6118:2003Estribo Convencional(kg) |
| P1=P4 | 2.069 | 1.822 | -247 | -11,9 | 1.810 |
| P2=P3 | 5.177 | 4.205 | -972 | -18,8 | 3.836 |
| P5=P6 | 5.693 | 11.335 | +5.642 | +99,1 | 9.495 |
| P7=P8 | 6.306 | 3.754 | -2552 | -40,7 | 3.495 |
| P9=P12 | 2.793 | 2.636 | -157 | -5,6 | 2.669 |
| P10=P11 | 4.338 | 3.191 | -1147 | -26,4 | 2.934 |
| TOTAL2x | 52.752 | 53.886 | +1.134 | +2,1 | 48.478 |
Observa-se o grande aumento de armaduras (quase 100%) que ocorreu nos pilares P5 e P6. O P5 e o P6 são pilares parede, seção qualquer em “L” e que resistem a grandes solicitações de cargas horizontais. Este acréscimo, de aproximadamente 5600 kg, compensou e ultrapassou todas as demais reduções de armaduras nos pilares retangulares.
Para analisar o efeito dos estribos neste pilares parede apresenta-se, abaixo, um quadro comparativo com as quantidades de armaduras longitudinais e transversais.
| PILAR | NBR6118:1980(kg) | NBR6118:2003(kg) | NBR6118:2003Estribo Convencional(kg) | ||||||
| Asl | Ast | Total | Asl | Ast | Total | Asl | Ast | Total | |
| P1=P4 | 1.519 | 550 | 2.069 | 1.260 | 562 | 1.822 | 1.260 | 550 | 1.810 |
| P2=P3 | 4.231 | 946 | 5.177 | 2.890 | 1.315 | 4.205 | 2.890 | 946 | 3.836 |
| P5=P6 | 3.994 | 1.699 | 5.693 | 7.796 | 3.539 | 11.335 | 7.796 | 1.699 | 9.495 |
| P7=P8 | 5.397 | 909 | 6.306 | 2.586 | 1.168 | 3.754 | 2.586 | 909 | 3.495 |
| P9=P12 | 2.087 | 706 | 2.793 | 1.963 | 673 | 2.636 | 1.963 | 706 | 2.669 |
| P10=P11 | 3.746 | 592 | 4.338 | 2.342 | 849 | 3.191 | 2.342 | 592 | 2.934 |
| Total2x | 41.948 | 10.804 | 52.752 | 37.674 | 16.212 | 53.886 | 37.674 | 10.804 | 48.478 |
Vamos comparar o total das armaduras longitudinais entre a NBR6118:2003 e NBR6118:1980. Houve uma redução de armaduras de (41.948-37.674) 4.274 Kg mesmo calculando-se o pilar parede segmentado em faixas.
Comparando as armaduras transversais temos um grande acréscimo de armaduras (16.212-10.804) de 5.408 kg.
No geral, para todos os pilares, predominantemente pilares parede, houve um acréscimo de 1.134 kg.
3.) Armaduras entre os lances - Seção qualquer
Vamos observar e comparar o que ocorre, lance a lance, com as quantidades de armaduras calculadas pelas duas normas.
3.1.) Pilares P5/P6
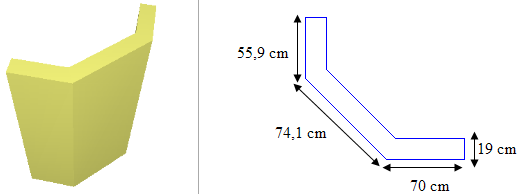
As dimensões do P5 e P6 são as seguintes:
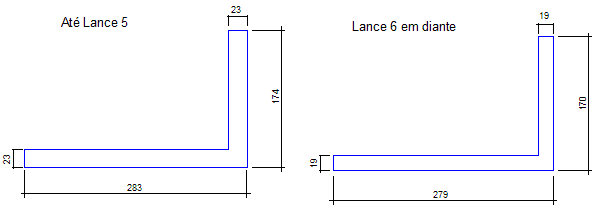
Note pelas dimensões que o P5/P6 são pilares paredes. Portanto as duas lâminas devem ser analisadas por procedimentos especiais conforme a NBR 6118:2003 (item 15.9) nos casos em que o λ de pelo menos uma de suas lâminas ultrapassar valor o de 35 (item 15.9.2 da NBR 6118:2003) o que depende, também, das vinculações entre as lâminas e do comprimento equivalente calculado a partir destas.
Os pilares P5 e P6 são elementos importantes para a resistência às cargas horizontais. Na direção Y (vertical, em planta) eles fazem parte do pórtico espacial mas existem poucas vigas ligando-os aos outros pilares, portanto, trabalham mais como pilares em balanço. Na direção X eles participam também ativamente para resistência da carga de vento, agora como pórtico plano, pois existe uma viga de alta rigidez na ligação entre eles. Duas forças normais formam um binário importante para resistir ao vento. Para a carga vertical, os pilares P5 e P6 absorvem uma carga vertical considerável, pois a área de influência deles é significativa.
O diagrama de momentos fletores típico deste pilar, carga de vento na direção Y, é apresentado na figura abaixo (para os primeiros lances). Este diagrama assemelha, de certa forma, ao diagrama de uma barra engastada em balanço. Também, mostramos o diagrama de força normal no pilar para o caso de carregamento vertical (peso próprio + cargas variáveis) e da força normal para o carregamento de vento na direção X.
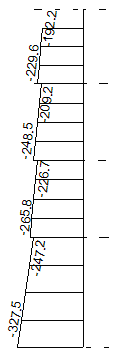 M - vento Y – tf*m M - vento Y – tf*m | 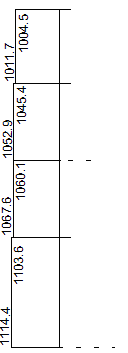 N - cargas verticais - tf N - cargas verticais - tf |  N - vento X - tf N - vento X - tf |
O diagrama de momentos fletores acima, principalmente para os lances inferiores, comprime ou traciona as fibras extremas do pilar. Este efeito é o que se pretende equacionar na análise localizada de pilares por lâminas/faixas.
A área do pilar P5 até o lance 5 é de 9.982 cm2. A taxa da compressão média (em valor característico) do pilar devido apenas a carga vertical, sem levar em conta os momentos fletores é de: 111,6 kgf/ cm2.
| Lance | P5 / P6As longitudinal (cm2) | ||||
| NBR6118:1980 | NBR6118:2003 | Diferença (%) | Seção Transversal(cm2) | λ da Lâmina crítica | |
| 12..24 | 47,1 | 37,7 | -20,0 | 8.170 | 46,8 |
| 11 | 47,1 | 53,4 | +13,4 | 8.170 | 46,8 |
| 10 | 47,1 | 41,6 | -11,7 | 8.170 | 46,8 |
| 9 | 47,1 | 71,2 | +51,2 | 8.170 | 46,8 |
| 8 | 47,1 | 118,6 | +151,8 | 8.170 | 46,8 |
| 7 | 47,1 | 178,9 | +279,8 | 8.170 | 46,8 |
| 6 | 81,7 | 238,8 | +192,3 | 8.170 | 46,8 |
| 5 | 50,3 | 140,7 | +179,7 | 9.982 | 39,8 |
| 4 | 73,6 | 164,9 | +124,0 | 9.982 | 36,2 |
| 3 | 90,8 | 238,8 | +163,0 | 9.982 | 43,1 |
| 2 | 128,7 | 407,4 | +216,6 | 9.982 | 47,8 |
Para o cálculo desta armadura longitudinal nas faixas, estamos utilizando o método do pilar-padrão acoplado a diagramas M, N, 1/r, item 15.8.3.3.4, isto é, calculando o k real de cada seção, método já bastante sofisticado, visando à obtenção de menores quantidades de armaduras longitudinais.
Para melhor entender onde houve variações mais significativas das armaduras, separamos na tabela abaixo as quantidades de armaduras longitudinais e transversais:
| Lance | P5 / P6(kg) | ||||||||
| NBR6118:1980 | NBR6118:2003 | Diferença (%) | |||||||
| Asl | Ast | Total | Asl | Ast | Total | Asl | Ast | Total | |
| 12..24 | 130 | 66 | 196 | 98 | 43 | 141 | -24,6 | -34,8 | -28,1 |
| 11 | 130 | 66 | 196 | 138 | 72 | 210 | +6,2 | +9,1 | +7,1 |
| 10 | 130 | 66 | 196 | 138 | 72 | 210 | +6,2 | +9,1 | +7,1 |
| 9 | 130 | 66 | 196 | 191 | 88 | 279 | +46,9 | +33,3 | +42,3 |
| 8 | 130 | 66 | 196 | 321 | 149 | 470 | +146,9 | +125,8 | +139,8 |
| 7 | 130 | 66 | 196 | 468 | 213 | 681 | +260,0 | +222,7 | +247,4 |
| 6 | 214 | 66 | 280 | 665 | 292 | 957 | +210,7 | +342,4 | +241,8 |
| 5 | 155 | 73 | 228 | 391 | 195 | 586 | +152,3 | +167,1 | +157,0 |
| 4 | 213 | 99 | 312 | 446 | 221 | 667 | +109,4 | +123,2 | +113,8 |
| 3 | 255 | 99 | 354 | 684 | 342 | 1.026 | +168,2 | +245,5 | +189,8 |
| 2 | 817 | 174 | 991 | 3.080 | 1.336 | 4.416 | +276,9 | +667,8 | +345,6 |
| Total | 3.994 | 1.699 | 5.693 | 7.796 | 3.539 | 11.335 | +95,2 | +108,3 | +99,1 |
Observando a coluna de “Diferenças”, podemos concluir que houve maior acréscimo nas armaduras transversais (estribos) do que nas longitudinais. Houve caso em que a armadura transversal (estribo) cresceu 667,8% !!!!! É o efeito do pilar-parede já comentado. Na norma de 1980, havia a prescrição de detalhar a armadura transversal como sendo 50% da armadura longitudinal. Esta recomendação era raramente obedecida pelos engenheiros estruturais. Agora, estamos calculando esta armadura como sendo 25% da armadura longitudinal. Para atender aos usuários que, eventualmente, optem por manipular esse valor de 25% (lembrando, porém, que a norma impõe este valor), criamos um critério de projeto específico, onde a porcentagem desejada é fornecida diretamente.
Vamos examinar com detalhes as armaduras desenhadas para o pilar 5 – lance 2.
| NBR6118:1980 | NBR6118:2003 |
 |  |
| 64 ɸ 16 (Asl = 128,7 cm2 - ρ = 1,29 %) | 83 ɸ 25 (Asl = 407,4 cm2 - ρ = 4,08 %) |
| Ast = 1,64 cm2 / m | Ast = 12,27 cm2 / m |
A figura acima mostra o desenho final das armaduras para o pilar P5-L2. Note a distribuição das armaduras na NBR6118: 2003 com a concentração de ferros nos extremos das lâminas do pilar. Pilares com estas dimensões e com a responsabilidade de resistir a esforços de vento, a partir desta nova norma, terão distribuição de armaduras semelhantes à apresentada acima. Este não é um detalhamento final para ser enviado a obra, mas sim, um desenho preliminar. Como as armaduras não estão simetricamente distribuídas, é necessária a identificação das cotas entre as diversas barras longitudinais.
Este pilar foi dimensionado folgadamente para a NBR 6118: 1980, mas para a nova norma, a taxa de armadura ficou no limite: 4,08%.
Importante ressaltar, mais uma vez, a diferença das armaduras transversais (estribos) se a NBR 6118:2003 for rigorosamente obedecida. O valor de Ast passou de 1,64 cm2/m para 12,27 cm2/m !!!! Este valor calculado serve apenas para efeito de comparação. Na prática, esta armadura transversal calculada inviabiliza o projeto deste pilar com as dimensões adotadas.
Conforme a figura acima, as faixas não necessitam ser, obrigatoriamente, retangulares. A faixa 4 é, também, uma seção qualquer. O quadro abaixo apresenta, com um pouco mais de detalhes, o que ocorre nas diversas faixas analisadas do P5-L2.
| Faixa | Mz/Mrdz | Nd (tf) | As (cm2) | ky | kz |
| 1 | 0,94 | 400,6 | 83,5 | 72,2 | 74,1 |
| 2 | 0,86 | 384,0 | 78,5 | 71,8 | 74,2 |
| 3 | 0,89 | 368,1 | 68,7 | 74,0 | 71,5 |
| 4 | 0,71 | 616,7 | 58,9 | 40,1 | 29,8 |
| 5 | 0,94 | 287,3 | 49,1 | 74,0 | 70,4 |
| 6 | 0,95 | 330,0 | 68,7 | 72,8 | 77,0 |
Para a obtenção do λy e λz , foi necessária a construção das curvas momento-curvatura. Abaixo apresentamos estas curvas típicas para estas faixas. Elas, simplificadamente, permitem o cálculo da rigidez real da seção considerando o concreto e as armaduras com suas relações não lineares. Empregamos este método mais refinado visando à redução das armaduras no dimensionamento.
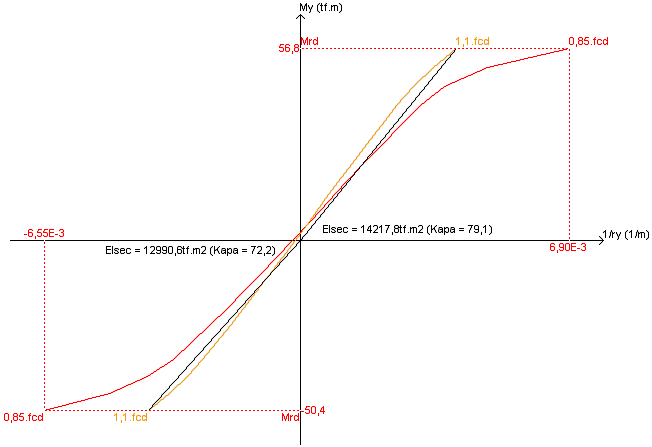
Relação Momento curvatura Pilar 5 Lance 2 Faixa 1 - direção My
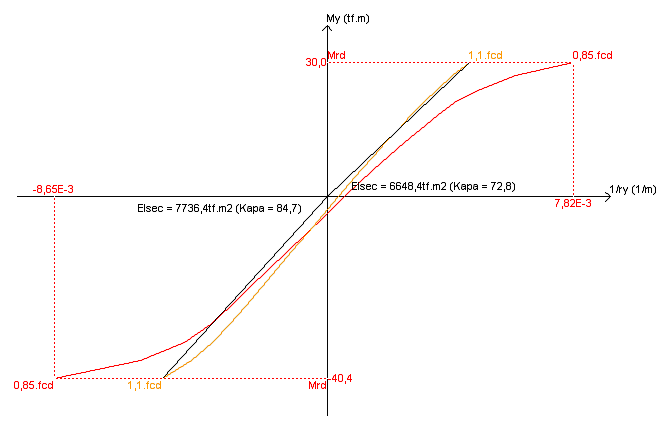
Relação Momento curvatura Pilar 5 Lance 2 Faixa 6 - direção My
Orientação eixo locais (faixa) “y” e “z”
Observar que o valor de Nd (esforço de cálculo) varia para as diversas faixas do pilar devido à parcela correspondente ao efeito dos momentos fletores atuantes nos extremos da seção. A força normal é maior na faixa 4, faixa mais central e menos sujeita ao efeito do momento fletor, fato a primeira vista incoerente, mas esta faixa 4 tem a seção transversal com maior área que as demais. O valor máximo de As ocorre na faixa 1, o que condiz com a intuição. Outro ponto interessante é a relação entre o ky e kz, rigidez secante adimensional, para a faixa 1. Como estes valores de kappa são valores da rigidez da seção divididos por um fator e por h2, eles resultam em valores próximos para as duas direções.
3.2.) Pilares P9/P12
Os pilares P9 e P12 são pilares não retangulares, mas não são pilares parede. Nenhuma lâmina do pilar atinge a condição de pilar parede conforme a figura abaixo.
Os pilares P9 e P12 tem as dimensões:
Os resultados de armaduras foram os seguintes:
| Lance | P9 / P12As longitudinal (cm2) | |||
| NBR6118:1980 | NBR6118:2003 | Diferença (%) | Área Seção Pilar (cm2) | |
| 12..23 | 20,4 | 18,8 | -7,8 | 4.086 |
| 11 | 20,4 | 18,8 | -7,8 | 4.086 |
| 10 | 20,4 | 20,4 | ----- | 4.086 |
| 9 | 20,4 | 22,0 | +7,8 | 4.086 |
| 8 | 20,4 | 23,6 | +15,7 | 4.086 |
| 7 | 20,4 | 25,1 | +23,0 | 4.086 |
| 6 | 41,7 | 31,9 | -23,5 | 4.086 |
| 5 | 52,3 | 52,3 | ----- | 4.086 |
| 4 | 92,2 | 106,8 | +15,8 | 4.086 |
| 3 | 48,3 | 61,4 | +27,1 | 4.086 |
| 2 | 68,4 | 52,3 | -23,5 | 4.086 |
Neste pilar observam-se pequenas alterações nos valores das armaduras para mais e/ou para menos ao longo dos seus lances. Isso se deve a diferenças na formulação do método da curvatura aproximada colocada pela norma NBR6118: 2003 e devido a consideração da excentricidade acidental da antiga norma, agora estamos utilizando o M1d,min. A pequena variação para menos a partir do lance 11 se deve a diminuição da porcentagem de As mínimo entre as normas (de 0,5% para 0,4%).
Para o cálculo desta armadura longitudinal, estamos utilizando o método tradicional do pilar-padrão com curvatura aproximada, 15.8.3.3.2. O método do λ aproximado não pode ser utilizado, pois ele é válido apenas para pilares retangulares.
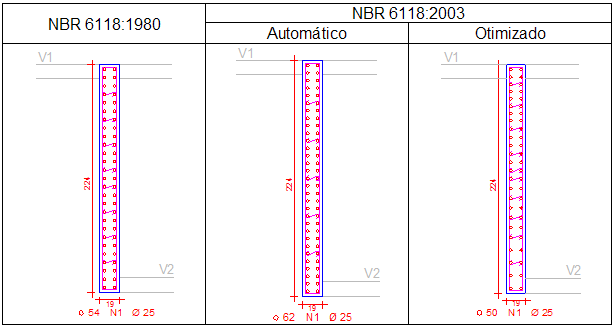
3.3.) Cálculo Automático e Otimizado
O sistema TQS já realiza, de forma automática, o cálculo das armaduras, dimensionamento e detalhamento para pilares parede com formato de seção transversal qualquer. Entretanto, neste processo de dimensionamento, utilizamos, as armaduras previamente configuradas e/ou definidas pelo usuário no perímetro da seção e que, na grande maioria dos casos, é uma armadura distribuída com espaçamento uniforme ao longo do perímetro do pilar.
Dependendo do formato do pilar, o usuário pode, no “Editor de Gráfico de Seções” dos sistemas TQS,configurar a locação das armaduras na seção transversal, concentrando os ferros nos extremos, mas esta condição é rara e, quando possível, deve-se levar em consideração, também, a possibilidade da execução deste tipo de configuração assimétrica.
O processo de dimensionamento do sistema de pilar de seção qualquer obedece ao espaçamento entre as barras fornecido pelo usuário. Como ocorre uma maior necessidade de armadura nos extremos do pilar, o resultado automático emitido pelo sistema dimensiona corretamente as faixas extremas e homogeneíza as faixas centrais com esta armadura. Portanto no processo automático, geralmente, as armaduras nas faixas centrais ficam um pouco maiores do que as necessárias.
Para não aumentar a quantidade de armaduras nas faixas internas, o usuário deve recorrer ao comando “Editor de Geometria, Esforços e Armaduras em Pilares” que realiza a verificação automática do efeito localizado em cada faixa do pilar, interativamente. É o que chamamos de processo otimizado. Evidentemente que o usuário tem um pouco mais de trabalho, mas com este procedimento, as armaduras ficam ajustadas para cada faixa.
Mostramos abaixo um quadro comparativo com as quantidades de armaduras nos dois casos, automático e otimizado (depois de editado):
| Lance | P5 / P6As longitudinal (cm2) | ||
| NBR6118:2003automático | NBR6118:2003 otimizado | Diferença (%) | |
| 12..24 | 47,1 | 37,7 | -20,0 |
| 11 | 72,3 | 53,4 | -26,1 |
| 10 | 55,0 | 41,6 | -24,4 |
| 9 | 88,4 | 71,2 | -19,5 |
| 8 | 148,8 | 118,6 | -20,3 |
| 7 | 217,1 | 178,9 | -17,6 |
| 6 | 339,3 | 238,8 | -29,6 |
| 5 | 140,7 | 140,7 | ----- |
| 4 | 193,0 | 164,9 | -14,6 |
| 3 | 282,7 | 238,8 | -15,5 |
| 2 | 540,0 | 407,4 | -24,5 |
| Peso | 15.256 kg | 11.335 kg | -25,7 |
No exemplo do P5 acima, a otimização das armaduras levou a uma redução das armaduras longitudinais calculadas automaticamente da ordem de 25,7%.
Para não ter que recorrer à otimização de forma interativa e, às vezes, trabalhosa, os sistemas TQS oferecem uma solução alternativa interessante. Dependendo do formato do pilar, o usuário pode, no “Editor de Gráfico de Seções” dos sistemas TQS,configurar a locação das armaduras na seção transversal, quando possível, concentrando ferros nos extremos. Deve-se levar em consideração, também, a possibilidade da execução deste tipo de configuração assimétrica.
Para utilizar este recurso também em seções retangulares, basta definir esta seção como uma seção qualquer, fornecendo as coordenadas da poligonal de contorno. Nas faixas extremas, definir posições de armaduras mais concentradas e, nas faixas centrais, posições de armaduras mais esparsas. Observe as figuras abaixo com detalhes do Editor Gráfico de Seções, como é possível concentrar armaduras nos extremos.
Detalhe da definição de concentração de armaduras no Editor Gráfico nos extremos de um pilar de seção qualquer:
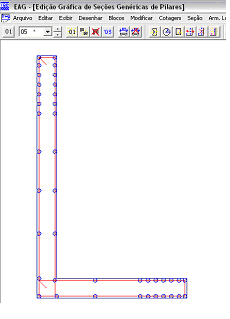
Detalhe da definição de concentração de armaduras no Editor Gráfico nos extremos de um pilar de seção retangular (definido como de seção qualquer):

Fazendo esta locação prévia de armaduras, mesmo para as seções retangulares, toda vez que os pilares forem reprocessados, as armaduras já estarão mais concentradas nos cantos automaticamente.
3.4.) Comparação do Cálculo do Pilar Parede pelo Método 1/r Aproximado e em Faixas
Apenas para estudar um pouco melhor o que ocorre nas armaduras do P5 – lance 2, e comparar as duas normas, vamos realizar o cálculo também pelo método da curvatura (1/r) aproximada (e sem a consideração dos efeitos localizados, sem as faixas) e do As efetivo já com a consideração dos efeitos localizados (dimensionamento por faixas).
| NBR 6118:1980 | NBR6118:2003AUTOMÁTICO | |
| As necessário(1/r aproximado) | 113,3 | 100,3 |
| As PP faixas | ------ | 407,4 |
O sistema TQS, desde que devidamente configurado nos critérios de projeto, pode realizar o cálculo do pilar apenas pelo método da curvatura (1/r) aproximada, o que não se recomenda por não estar atendendo a atual norma NBR 6118:2003, mas que, apenas para efeitos de comparação, levaria a uma armadura menor, próxima daquela calculada pela NBR6118:1980, o que está coerente com as mudanças na formulação deste método (1/r aproximado).
4.) Armaduras entre os Lances - Seção Retangular
Nestes pilares houve uma predominância na redução de armaduras. Os lances que tiveram o mesmo dimensionamento ou diferenças pouco significativas não serão aqui apresentados.
4.1.) Pilares P7/P8
O P7 e o P8 tem as dimensões:
Lance 5 em diante

Até Lance 4

Estes pilares são pilares parede, pois uma das dimensões da seção transversal ultrapassa a outra em mais de 5 vezes. Note a locação do P7/P8 na planta de formas abaixo:
Os pilares P7 e P8 são elementos que estão ligados a outros pilares através de vigas e, portanto, funcionam também parcialmente aporticados para a direção Y (vertical). Eles resistem às cargas horizontais, mas o comportamento do diagrama de momentos fletores é mais próximo de um pórtico e mais distante de pilares em balanço. Através das vigas, há uma transferência de cargas entre os pilares reduzindo os valores dos momentos fletores nos pilares. A rigidez do P7 nos lances inferiores, direção Y, é de 28,3% da rigidez do pilar P5. Para a direção X, o pilar pouco colabora, pois a sua rigidez é pequena. Para as cargas verticais, os pilares P7 e P8 não absorvem tanta carga, pois sua área de influência não é significativa.
O diagrama de momentos fletores típico destes pilares, vento na direção Y é apresentado abaixo (para os primeiros lances). Também mostramos o diagrama de cargas verticais para o carregamento 1 (cargas de peso próprio e variáveis).
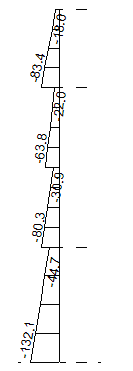 M - vento Y - tf*m M - vento Y - tf*m | 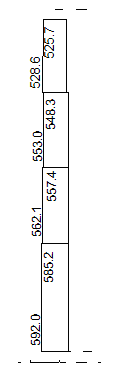 Força Normal – cargas verticais - tf Força Normal – cargas verticais - tf |
Como se pode notar, este pilar com dimensões avantajadas absorveu um momento fletor razoável para carga de vento na direção Y, mas muito inferior ao momento fletor do pilar P5 (327 tf*m).
A tensão de compressão média do pilar no lance inferior,apenas para carga vertical, valor característico, é de: 94,0 kgf/cm2.
As armaduras encontradas, ao longo dos lances foram as seguintes.
| Lance | P7 / P8As longitudinal (cm2) | ||||
| NBR6118:1980 | NBR6118:2003 | Diferença(%) | Seção Transversal (cm2) | λ da Lâmina | |
| 24 | 28,3 | 29,8 | +5,3 | 3.990 | 52,9 |
| 18..23 | 15,7 | 15,7 | ----- | 3.990 | 52,9 |
| 17 | 24,5 | 15,7 | -36,0 | 3.990 | 52,9 |
| 16 | 44,2 | 15,7 | -64,5 | 3.990 | 52,9 |
| 15 | 48,3 | 15,7 | -67,5 | 3.990 | 52,9 |
| 14 | 68,4 | 15,7 | -77,0 | 3.990 | 52,9 |
| 13 | 88,0 | 19,6 | -77,8 | 3.990 | 52,9 |
| 12 | 106,8 | 32,2 | -69,9 | 3.990 | 52,9 |
| 11 | 119,4 | 44,2 | -63,0 | 3.990 | 52,9 |
| 10 | 119,4 | 32,2 | -73,0 | 3.990 | 52,9 |
| 9 | 125,7 | 50,3 | -60,0 | 3.990 | 52,9 |
| 8 | 131,9 | 62,8 | -52,4 | 3.990 | 52,9 |
| 7 | 117,8 | 98,2 | -16,6 | 3.990 | 52,9 |
| 6 | 137,4 | 108,0 | -21,4 | 3.990 | 52,9 |
| 5 | 225,8 | 157,1 | -30,4 | 3.990 | 54,7 |
| 4 | 150,8 | 32,2 | -78,6 | 6.300 | 69,3 |
| 3 | 100,5 | 36,2 | -64,0 | 6.300 | 69,3 |
| 2 | 60,3 | 36,2 | -40,0 | 6.300 | 45 |
Na tabela acima, observa-se para os diversos lances uma expressiva redução de armaduras. As explicações para estas reduções já foram aqui apresentadas através de mensagem anterior e que colocamos como anexo a este artigo.
Embora o P7/P8 tenha dimensões de pilar parede (dimensão maior > 5 X a dimensão menor), o efeito dos momentos fletores nas lâminas / faixas do pilar não foi muito intenso, pois o momento fletor não é muito elevado.
Para o cálculo desta armadura longitudinal nas faixas, estamos utilizando o método do pilar-padrão acoplado a diagramas M, N, 1/r, item 15.8.3.3.4, isto é, calculando o k real de cada seção, método já bastante sofisticado, visando à economia nas quantidades de armaduras longitudinais.
Para melhor entender onde ocorreram variações mais significativas das armaduras, separamos na tabela abaixo as quantidades de armaduras longitudinais e transversais:
| Lance | P7 / P8(kg) | ||||||||
| NBR6118:1980 | NBR6118:2003 | Diferenças(%) | |||||||
| Asl | Ast | Total | Asl | Ast | Total | Asl | Ast | Total | |
| 24 | 65 | 35 | 100 | 69 | 38 | 107 | +6,2 | +8,6 | +7,0 |
| 18..23 | 41 | 27 | 68 | 41 | 27 | 68 | ---- | ---- | ---- |
| 17 | 66 | 33 | 99 | 41 | 27 | 68 | -37,9 | -18,2 | -31,3 |
| 16 | 120 | 34 | 154 | 41 | 27 | 68 | -65,8 | -20,6 | -55,8 |
| 15 | 131 | 36 | 167 | 41 | 27 | 68 | -68,7 | -25,0 | -59,3 |
| 14 | 179 | 45 | 224 | 41 | 27 | 68 | -77,1 | -40,0 | -69,6 |
| 13 | 249 | 40 | 289 | 53 | 32 | 85 | -78,7 | -20,0 | -70,6 |
| 12 | 292 | 45 | 337 | 88 | 34 | 122 | -69,9 | -24,4 | -63,8 |
| 11 | 331 | 33 | 364 | 116 | 50 | 166 | -65,0 | +51,5 | -54,4 |
| 10 | 337 | 33 | 370 | 99 | 40 | 139 | -70,6 | +21,2 | -62,4 |
| 9 | 347 | 33 | 380 | 140 | 49 | 189 | -59,7 | +48,5 | -50,3 |
| 8 | 364 | 38 | 402 | 169 | 66 | 235 | -53,6 | +73,7 | -41,5 |
| 7 | 368 | 67 | 435 | 292 | 124 | 416 | -20,7 | +85,1 | -4,4 |
| 6 | 396 | 56 | 452 | 321 | 132 | 453 | -18,9 | +135,7 | 0,2 |
| 5 | 616 | 59 | 675 | 443 | 175 | 618 | -28,1 | +196,6 | -8,4 |
| 4 | 586 | 41 | 627 | 86 | 41 | 127 | -85,3 | 0,0 | -79,7 |
| 3 | 336 | 43 | 379 | 99 | 41 | 140 | -70,5 | -4,7 | -63,1 |
| 2 | 368 | 76 | 444 | 201 | 76 | 277 | -45,4 | ---- | -37,6 |
| Total | 5.397 | 909 | 6.306 | 2.586 | 1.168 | 3.754 | -52,1 | +28,5 | -40,5 |
Observando a coluna de “Diferenças”, podemos concluir que houve uma redução geral nas armaduras longitudinais. No lance 4 a armadura reduziu 85% !!! As armaduras transversais (estribos) cresceram de forma significativa para quase todos os lances. Houve caso em que a armadura cresceu quase 200% !!!!! É o efeito do pilar-parede já comentado. Mesmo com redução da armadura longitudinal, os estribos cresceram. Na norma de 1980, havia a prescrição de detalhar a armadura transversal como sendo 50% da armadura longitudinal. Esta recomendação era raramente obedecida pelos engenheiros estruturais. Agora, estamos calculando esta armadura como sendo 25% da armadura longitudinal. Para atender aos usuários que, eventualmente, não concordam com os 25%, criamos um critério de projeto específico, onde a porcentagem desejada é fornecida diretamente.
Vamos examinar com detalhes as armaduras desenhadas para o pilar 8 – lance 3.
Pilar P8 Lance 3 - Detalhe das armaduras longitudinais
| NBR6118:1980 | NBR6118:2003 |
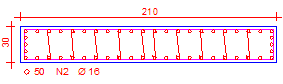 |  |
| 50 ɸ 16 (Asl =100,5 cm2 - ρ = 1,60 %) | 18 ɸ 16 (As = 36,2 cm2 - ρ = 0,57 %) |
| Ast = 1,64 cm2 / m | Ast = 2,23 cm2 / m |
A figura acima mostra o desenho final das armaduras para o pilar P8-L3. A distribuição das armaduras na NBR6118: 2003, com uma pequena concentração de ferros nos extremos das lâminas do pilar, é semelhante à da NBR6118: 1980. Pilares com estas dimensões, adequadas, mesmo com a consideração dos efeitos localizados de pilares parede, não apresentam variações significativas de armaduras nos extremos.
Vamos examinar o que ocorre em cada faixa do pilar.
| Faixa | Mz/Mrdz | Nd (tf) | As (cm2) | ky | kz |
| 1 | 0,54 | 278,9 | 14,1 | 58,0 | 58,1 |
| 2 | 0,57 | 274,8 | 8,0 | 56,9 | 58,3 |
| 3 | 0,75 | 324,5 | 14,1 | 61,6 | 63,0 |
Para a obtenção do λy e λz , foi necessária a construção das curvas momento-curvatura. Abaixo apresentamos estas curvas típicas para estas faixas. Elas, simplificadamente, permitem o cálculo da rigidez real da seção considerando o concreto e as armaduras com suas relações não lineares. Empregamos este método mais refinado visando à redução das armaduras no dimensionamento.
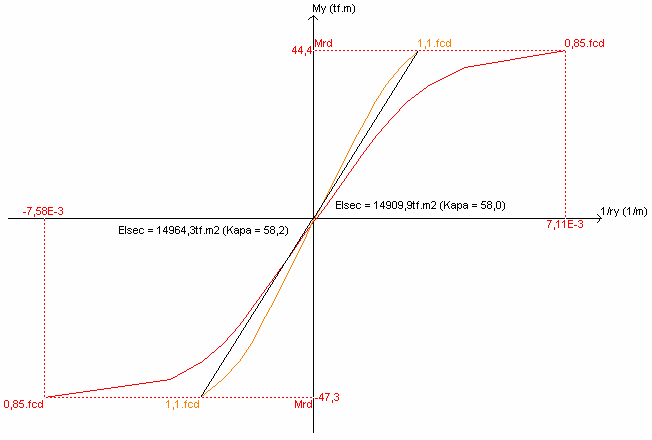
Relação Momento Curvatura Pilar 8 Lance 3 Faixa 1 - direção My
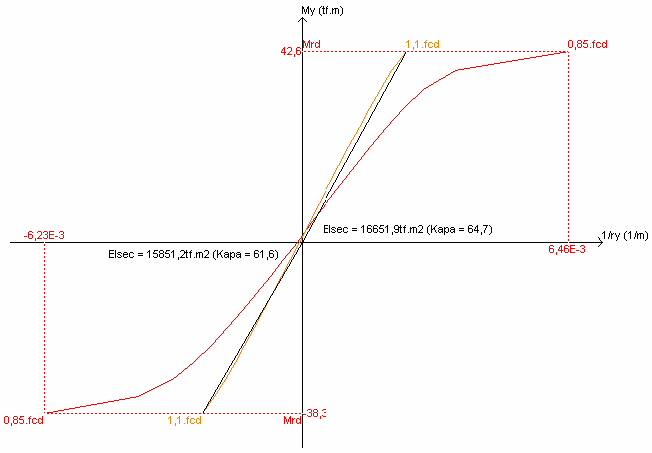
Relação Momento Curvatura Pilar 8 Lance 3 Faixa 3 - direção My
Orientação eixo locais (faixa) “y” e “z”
Observar que o valor de Nd (esforço de cálculo) varia para as diversas faixas do pilar devido à parcela correspondente ao efeito dos momentos fletores atuantes nos extremos da seção. A força normal é maior na faixa 3, faixa mais a direita. O valor máximo de As ocorre nas faixas 1 e 3. Outro ponto interessante é a relação entre o ky e kz, rigidez secante adimensional, para a faixa 3. Como estes valores de kappa são valores da rigidez relativa da seção, observa-se que na faixa de maior Nd é onde ocorreu uma maior rigidez.
4.2.) Pilares P2/P3
O P2 e o P3 tem as seguintes dimensões:

O P2 e o P3 também são pilares parede.
As armaduras encontradas, ao longo dos lances, para estes pilares foram as seguintes.
| Lance | P2 / P3Asl (cm2) | ||||
| NBR6118:1980 | NBR6118:2003 | Diferença(%) | Seção Transversal (cm2) | λ da Lâmina | |
| 26 | 29,5 | 29,5 | ----- | 950 | 53,3 |
| 25 | 28,3 | 39,3 | +38,9 | 4.256 | 52,9 |
| 14..24 | 17,3 | 17,3 | ----- | 4.256 | 52,9 |
| 13 | 22,1 | 17,3 | -21,7 | 4.256 | 52,9 |
| 12 | 44,2 | 17,3 | -60,9 | 4.256 | 52,9 |
| 11 | 44,2 | 17,3 | -60,9 | 4.256 | 52,9 |
| 10 | 48,3 | 17,3 | -64,2 | 4.256 | 52,9 |
| 9 | 62,8 | 17,3 | -72,4 | 4.256 | 52,9 |
| 8 | 62,8 | 17,3 | -72,4 | 4.256 | 52,9 |
| 7 | 62,8 | 18,8 | -70,1 | 4.256 | 52,9 |
| 6 | 75,4 | 22,1 | -70,7 | 4.256 | 52,9 |
| 5 | 69,1 | 40,8 | -41,0 | 4.256 | 55,2 |
| 4 | 75,4 | 46,5 | -38,3 | 4.256 | 54,7 |
| 3 | 119,4 | 69,1 | -42,1 | 4.256 | 54,7 |
| 2 | 265,1 | 245,4 | -7,4 | 4.256 | 83,9 |
Houve uma redução generalizada de armaduras da ordem de 60% sendo que, para o lance mais carregado (lance 2) a redução foi de apenas 7.4%.
Para o cálculo desta armadura longitudinal por faixas, também estamos utilizando o método do pilar-padrão acoplado a diagramas M, N, 1/r, item 15.8.3.3.4, isto é, calculando o λ real de cada faixa, visando a obtenção de menores quantidades de armaduras longitudinais.
4.3.) Cálculo Automático x Otimizado
Aqui valem as mesmas observações já apresentadas no item 3.3). O sistema TQS já realiza, de forma automática, o cálculo das armaduras, dimensionamento e detalhamento para pilares parede formato retangular. O alojamento automático das barras é sempre regular com espaçamentos constantes entre as barras.
O processo de dimensionamento do sistema de pilar de seção retangular obedece ao espaçamento constante entre as barras. Como ocorre uma maior necessidade de armadura nos extremos do pilar, o resultado automático emitido pelo sistema dimensiona corretamente as faixas extremas e superdimensiona as faixas centrais. Portanto no processo automático, geralmente, as armaduras nas faixas centrais ficam maiores do que as necessárias.
Para não aumentar a quantidade de armaduras nas faixas internas, o usuário deve recorrer ao “Editor de Geometria, Esforços e Armaduras de Pilares” que realiza a verificação automática do efeito localizado em cada faixa do pilar, interativamente. É o que chamamos de processo otimizado. Evidentemente que o usuário tem um pouco mais de trabalho, mas com este procedimento, as armaduras ficam ajustadas para cada faixa.
Mostramos abaixo um quadro comparativo com as quantidades de armaduras nos dois casos, automático e otimizado (depois de editado):
| Lance | P2 / P3Asl (cm2) | ||
| NBR6118:2003automático | NBR6118:2003otimizado | Diferença(%) | |
| 26 | 29,5 | 29,5 | ----- |
| 25 | 47,1 | 39,3 | -16,6 |
| 8..24 | 17,3 | 17,3 | ----- |
| 7 | 18,8 | 18,8 | ----- |
| 6 | 22,1 | 22,1 | ----- |
| 5 | 49,1 | 40,8 | -16,9 |
| 4 | 56,3 | 46,5 | -17,4 |
| 3 | 88,0 | 69,1 | -21,5 |
| 2 | 304,3 | 245,4 | -19,4 |
| 1 | 25,1 | 25,1 | ----- |
| Peso | 5.177 kg | 4.205 kg | -18,8 |
Esta otimização de armaduras resultou, para os pilares P2 e P3 mostrados acima, em economia de armaduras da ordem de 18.8 %.
O detalhamento do pilar 2, lance 2 ficou conforme o desenho abaixo:
Este não é um desenho final para ser enviado a obra, mas sim, um desenho preliminar. Como as armaduras não estão simetricamente distribuídas, é necessária a identificação das cotas entre as diversas barras longitudinais.
Vamos analisar o que ocorre em cada faixa de dimensionamento.
| Faixa | Mz/Mrdz | Nd (tf) | As (cm2) | λy | λz | Caso |
| 1 | 0,94 | 168,9 | 49,1 | 68,4 | 53,3 | 30 |
| 2 | 0,88 | 164,5 | 49,1 | 52,1 | 52,2 | 27 |
| 3 | 0,96 | 185,7 | 58,9 | 58,2 | 57,7 | 29 |
| 4 | 0,84 | 208,6 | 78,5 | 77,9 | 66,8 | 29 |
As faixas no pilar foram distribuídas da seguinte forma:
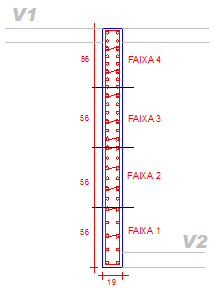
Observe que a armadura final otimizada é inferior à obtida pela antiga norma. A não simetria, apesar de não ser comum em obra, possibilita um arranjo de armadura onde esta é necessária e, conseqüentemente, mais economia, sendo que este tipo de arranjo assimétrico, na análise dos efeitos localizados, foi utilizado. Poderia ter sido adotado um arranjo mais simétrico, em que as armaduras da faixa da extremidade mais solicitada seriam também colocadas na faixa menos solicitada, levando a uma maior segurança, principalmente na execução do pilar, e a uma maior armadura total.
4.4.) Análise Detalhada do P2 – Lance 2
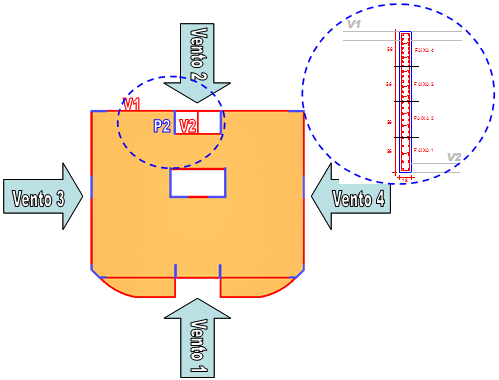
A diferença nos valores de armaduras encontrados para as faixas do pilar parede P2 – lance 2 não é intuitiva mas é devido à decomposição final dos esforços, dos diversos casos atuantes, na análise dos efeitos localizados. Observe as figuras abaixo:
Os principais valores de solicitações (características) no lance são:
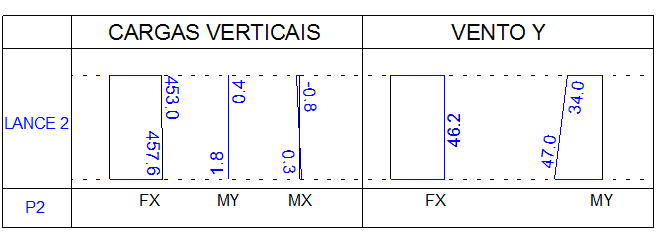
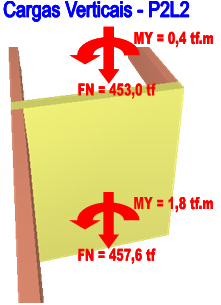
- As cargas verticais apresentam valores ligeiramente diferentes nas duas extremidades da lâmina deste pilar devido ao momento y correspondente a estes esforços (My = 1,8 tf*m na base) o que virá a influenciar na decomposição dos esforços nas faixas 1 e 4 situadas na extremidade desta lâmina;
- Os esforços de vento na direção y são simétricos, ora comprimindo a seção deste pilar (vento 1), ora tracionando esta seção (vento 2);
- O caso 29, combinação das cargas verticais com o vento 1 (responsável por um esforço normal adicional de 46,2 tf) gera a pior condição de compressão para a faixa 4 deste pilar;
- O caso 30, combinação das cargas verticais com o vento 2 (que gera um esforço adicional de tração de 46,2 tf) tem os esforços de cargas verticais totais aliviados, mas quando decompostos por faixa levam ao esforço crítico de compressão para o dimensionamento da faixa 1;
Solicitações características no lance para os casos de carregamento 29 e 30:
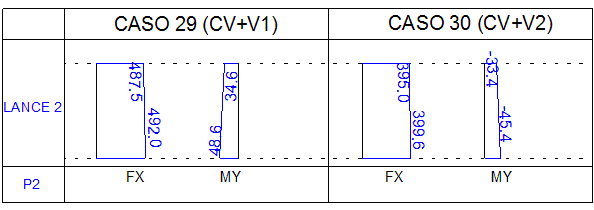
- A decomposição final destes esforços, nas faixas desta lâmina, resulta em esforços críticos com origem em casos diferentes (casos 29 ou 30), como apresentados na figura abaixo:
- Valores de Nd (tf) das faixas do Pilar P2 Lance 2 para os casos de carregamento 24, 27, 29 e 30
 | FAIXA | CASO 24(CV) | CASO 27(CV+V3) | CASO 29(CV+V1) | CASO 30(CV+V2) |
| 4 | 160,1 | 167,0 | 208,6 | 103,4 | |
| 3 | 159,6 | 165,7 | 185,7 | 125,2 | |
| 2 | 159,1 | 164,5 | 162,8 | 147,1 | |
| 1 | 158,6 | 163,3 | 140,0 | 168,9 | |
| Tot | 637,4 | 660,5 | 697,1 | 544,6 |
5.) Conclusões
Antes da apresentação das principais conclusões, vamos apresentar a planta de formas do pavimento tipo novamente para recordar a locação dos pilares. As conclusões deste processamento são:

5.1) Os resultados aqui mostrados são representativos de um edifício de altura mediana, da ordem de 75m. Para edifícios maiores, as conclusões aqui apresentadas terão um maior significado e relevância.
5.2) As quantidades totais de armaduras neste edifício ficaram com valores muito próximos na comparação entre a NBR 6118:1980 e NBR 6118:2003.
5.3) Os resultados comparativos das quantidades de armaduras neste edifício são, em alguns casos particulares, intrigantes. Deve-se sempre ter em mente que, ao se comparar armaduras, na grande maioria dos casos, a redução da capacidade resistente do pilar não é diretamente proporcional apenas à quantidade de armaduras, isto é, um pilar com 1% de armadura não tem a metade da capacidade resistente do pilar com 2% de armadura. Deve-se levar em conta a presença significativa do material concreto.
5.4) É importante lembrar que os processamentos foram realizados com a incorporação das sugestões do eng. Francisco P. Graziano, formulada no ENECE/2004 (anteriormente apresentadas pelo prof. Flávio Costa, prof. da Unicamp) e que provoca um aumento de armadura em alguns lances.
5.5) A consideração do comprimento do pé-direito não está obedecendo exatamente às prescrições da NBR6118: 2003 (entre faces + altura do pilar na direção considerada) mas, de forma mais conservadora, está sendo assumido como sendo a distância entre os eixos das vigas (superior e inferior).
5.6) Os itens acima, 5.4) e 5.5) vem de encontro ao aumento das quantidades de armaduras dos pilares. Estas foram, também, razões que provocaram o distanciamento destes valores totais de armaduras com os já apresentados durante os cursos que ministramos por todo o país.
5.7) A drástica redução das armaduras dos pilares P2-L6 (70%), do P7-L10 (73%) etc. acompanha a conclusão já apresentada no e-mail enviado a ComunidadeTQS pelo eng. Alio E. Kimura há alguns meses (Anexo a este relatório) e, também, está de acordo com a apresentação da palestra proferida pelo eng. Francisco P. Graziano no ENECE/2004.
5.8) A grande variabilidade nas quantidades das armaduras longitudinais é devida a melhores critérios de cálculo dos efeitos de 2a ordem e tambem a adoção do M1d,min para o tratamento das imperfeições geométricas locais. O M1d,min é um procedimento consagrado na norma americana ACI-318. Como o ACI-318 também prescreve a armadura mínima de 1% da seção, criamos no sistema TQS um critério novo para esta consideração (mais conservador que a NBR6118:2003). Utilizando a armadura mínima de 1%, as diferenças nas armaduras longitudinais se reduzem significativamente.
5.9) A substancial elevação das armaduras no P5-L2 em forma de “L”, confirma a alteração radical no projeto de pilares-parede conforme item 15.9 da NBR 6118:2003.
5.10) Embora a quantidade total de armaduras não tenha sido alterada de forma significativa, nota-se, do ponto de vista global, uma diminuição das armaduras dos pilares retangulares e um aumento dos pilares P5 e P6 de seção “L”.
5.11) Os pilares parede P5 e P6 devido a sua rigidez absorvem a maior parte dos momentos fletores oriundos dos esforços horizontais nas direções X e Y. Eles concentram os maiores momentos fletores devido a cargas horizontais funcionando como pilares parcialmente em balanço para estas cargas. Este é um procedimento comum em edifícios altos. Estes momentos fletores provocam elevadas forças normais nas faixas extremas do pilar e, conseqüentemente, elevadas armaduras longitudinais. A partir da NBR 6118:2003, estes pilares deverão ter suas dimensões aumentadas para que seja possível o seu dimensionamento considerando os efeitos localizados.
5.12) Nos lances mais solicitados, os pilares parede concentram a necessidade de armaduras nos seus extremos. Como, geralmente, estas armaduras tiveram aumentos significativos, para se realizar um projeto econômico conforme a NBR 6118:2003, elas devem ser detalhadas com espaçamentos variáveis entre as diversas faixas.
5.13) O cálculo de pilares parede por faixas, geralmente, aumenta a armadura nas faixas extremas do pilar. É muito importante recorrer a métodos de cálculo mais elaborados visando à economia da quantidade de armaduras. Neste nosso exemplo, assim como é recomendação padrão nos sistemas TQS, o método utilizado para a análise destas faixas é o pilar-padrão acoplado a diagramas M, N, 1/r, item 15.8.3.3.4. Embora o tempo de processamento aumente um pouco devido a necessidade da elaboração das relações momento-curvatura para todas as faixas, o resultado é compensador do ponto de vista da redução de armaduras, tornando o projeto mais econômico e competitivo.
5.14) A antiga norma NBR 6118:1980 estabelecia para a armadura transversal de pilares parede, o valor correspondente a 50% da armadura longitudinal. Apesar da redução prescrita na nova NBR 6118: 2003, no quesito de estribos em pilar parede (25% da armadura longitudinal), ainda ocorre um aumento significativo na quantidade total das armaduras de pilares neste projeto onde os pilares parede são predominantes, quando seguimos plenamente esta prescrição. Devemos lembrar que a recomendação da NBR6118: 1980 não era, geralmente, respeitada pelos projetistas. Está em estudo, pelos engenheiros Ricardo França e Alio Kimura, um critério de cálculo mais racional para estribos de pilares parede.
5.15) A elevada armadura para estribos em pilar parede pode, muitas vezes, inviabilizar o detalhamento do pilar com as dimensões desejadas. Embora outros quesitos de norma possam estar atendidos (estabilidade, equilíbrio da seção, taxa de armadura longitudinal etc.), estribos com diâmetros elevados ou com espaçamentos reduzidos, podem obrigar a alteração nas dimensões do pilar. Com maior largura, as lâminas terão menores armaduras longitudinais e menos estribos. Em alguns casos, aumentando-se a largura da lâmina, o pilar pode até ser dispensado de cálculo como pilar parede.
5.16) Nesse nosso exemplo, o pilar P5, lance 2, possui a necessidade de armadura de estribos de 12,27 cm2/m. É quase impossível detalhar os estribos de um pilar com esta área (bitola de 12.5 mm cada 10 cm). Deixamos o exemplo desta forma apenas para alertar aos usuários sobre o problema. Outro ponto importante na alteração dos estribos de pilar parede para bitolas maiores é a conseqüente redução do braço de alavanca entre os baricentros das barras longitudinais. Caso se opte por utilizar os 25% de armadura transversal conforme prescrições de norma, é importante trabalhar com dimensões maiores dos pilares parede para a conseqüente redução das armaduras longitudinais. Os sistemas TQS possuem critério específico para o fornecimento de taxa de armadura transversal menor que os 25% (obviamente, contra a norma).
5.17) Mesmo calculando-se todos os pilares como pilar parede, por faixas, se desprezarmos os estribos de pilar parede, teremos uma economia de armaduras da ordem de 10%, neste exemplo.
5.18) Devido a complexidade no dimensionamento de pilares parede, conforme prescrições na NBR 6118:2003, especialmente os pilares em forma de “L”, “U”, “C” etc. que mais resistem às cargas horizontais, o projeto de pilares realizado por processos manuais em edifícios altos fica praticamente inviabilizado, tendo-se que recorrer ao cálculo informatizado por sofisticadas ferramentas computacionais.
5.19) O projeto de pilares de seção transversal qualquer pela NBR 6118:1980 era, inegavelmente, muito simplificado e fora da realidade. Podem-se questionar os procedimentos da NBR6118: 2003, mas depois de tantos estudos sobre pilares, já não é mais admissível aceitar o projeto de pilares parede, especialmente os de seção qualquer, de alta responsabilidade, como era indicado na norma antiga. Apenas para recordar algumas hipóteses básicas, o pilar parede de seção qualquer não tem a forma retangular e, também, não tem a armadura simétrica, portanto, o seu cálculo não pode ser feito pelo método da curvatura aproximada e nem do kappa aproximado. Na falta de uma melhor alternativa, é recomendado e aconselhável que o pilar seja discretizado em faixas para tal dimensionamento. Este é um procedimento pioneiro e inédito da nossa NBR6118: 2003.
Eng. Hermes Luiz Bolinelli Jr.
Eng. Nelson Covas
TQS Informática Ltda.
Para acessar o artigo na íntrega, utilize o endereço abaixo:
http://www.tqs.com.br/downloads/comparativopilares.zip
