Método Geral para análise local de pilares

Eng. Nelson Covas / Eng. Alio Kimura

TQS Informática Ltda

I. Introdução

Descreve-se a seguir, como o item tão relevante “Dimensionamento de Pilares” será tratado pelos sistemas TQS, perante às prescrições da nova norma NBR6118:2003 “Projeto de estruturas de concreto - procedimentos".

O objetivo do texto será de demonstrar, de forma clara e objetiva, como os diversos conceitos abordados pela nova norma, mais especificamente das seções 11 “Ações” e 15 “Instabilidade e efeitos de segunda ordem”, serão aplicados nos sistemas e quais recursos estarão disponíveis nos programas.

Um maior enfoque será dado a análise dos efeitos locais em pilares segundo o Método Geral.

II. A nova NBR6118

De uma forma geral, pode-se afirmar que uma das grandes modificações da nova norma com relação à antiga NBR6118:1980, é a apresentação de maneira mais explícita e incisiva de como as não-linearidades física e geométrica devem ser consideradas na elaboração de projetos estruturais de um edifício.

No item 15.3 “Princípios básicos de cálculo”, por exemplo, descreve-se de forma clara:

Existem diversas maneiras de considerar este comportamento não-linear. Em alguns casos, uma simples redução de rigidez EI já pode ser suficiente. No entanto, torna-se cada vez mais evidente a importância das análises não-lineares que, sem dúvida, passarão a ficar mais comuns no dia-a-dia de um engenheiro estrutural.

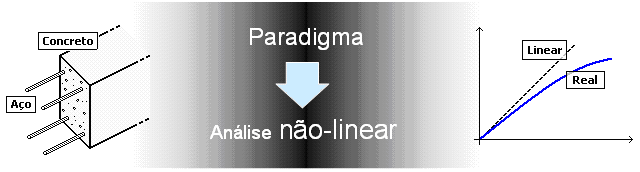
III. Efeitos globais, locais e localizados de 2ª ordem

De uma maneira geral, os efeitos de 2ª ordem são obtidos através de uma análise na qual o equilíbrio da estrutura é definido e verificado na sua configuração deformada, e só podem ser desprezados quando não acrescentarem mais de 10% nas solicitações relevantes.

No item 15.4.1 “Efeitos globais, locais e localizados de 2ª ordem” da NBR6118:2003, os diferentes e possíveis efeitos de 2ª ordem em uma estrutura são muito bem definidos. Através de uma rápida análise das deformações que um edifício de concreto-armado está sujeito quando submetido a ações de cargas verticais e horizontais, fica fácil compreendê-los e a diferenciá-los.

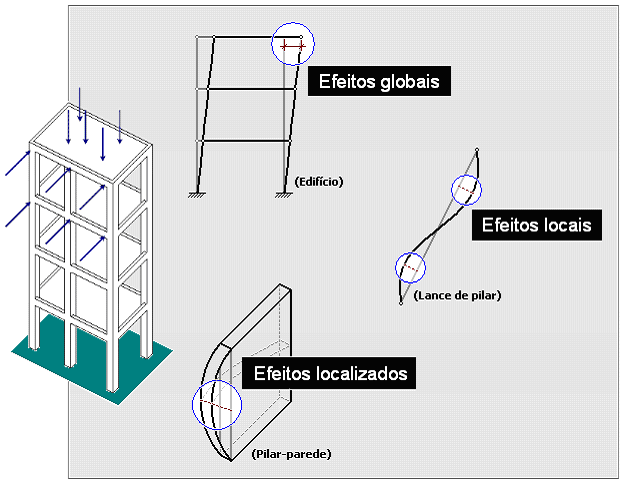
Com relação aos esforços, no entanto, esta percepção não é tão direta assim. Vamos então, ilustrar quais são as influências dos efeitos globais e locais nos esforços em pilares de um edifício de concreto-armado, simulado através de um pórtico espacial.

Inicialmente, vamos partir de uma análise em 1ª ordem (equilíbrio na configuração indeformada), na qual consegue-se obter a força normal e os momentos de 1ª ordem no topo e na base em cada um dos lances dos pilares.

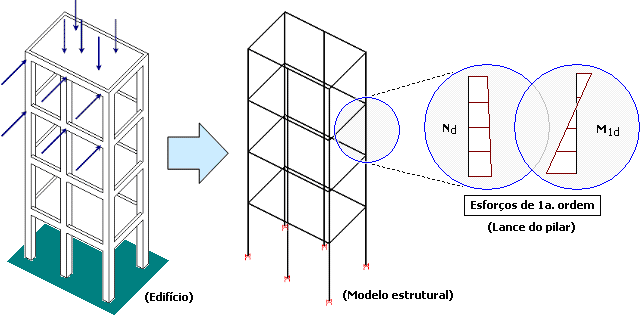
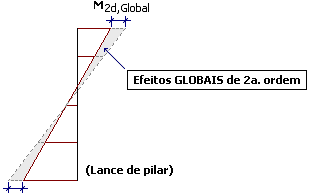	A análise global em 2ª ordem, seja através do coeficiente ɣz ou do P-Delta, fornecerá esforços adicionais somente nos extremos das barras, isto é, no topo e na base dos lances dos pilares.
Já, a análise local em 2ª ordem fornecerá esforços adicionais ao longo dos lances dos pilares.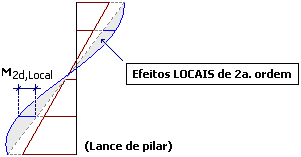

Os efeitos locais de 2ª ordem dependem dos esforços de 1ª ordem, bem como dos esforços globais de 2ª ordem. E portanto, é fundamental que se utilize um modelo estrutural adequado e adaptado à realidade das estruturas de concreto-armado na obtenção dos mesmos. Modelos puramente elásticos podem levar a resultados contra a segurança.

A seguir, nos capítulos subsequentes, será mostrado como os efeitos locais que atuam ao longo do lance serão calculados. Os modelos e métodos para obtenção dos efeitos globais de 2ª ordem, já foram explicados com detalhes pelo eng. Abram na Comunidade-TQS. Quanto aos efeitos localizados, eles já estão sendo adaptados aos programas e serão tema de um outro artigo.

IV. Efeitos locais de 2ª ordem

Quanto maior o índice de esbeltez do pilar (λ) ou maior a força normal atuante (N_d), maiores serão os efeitos locais de 2ª ordem, que por sua vez, somente poderão ser desprezados quando λ < λ₁ (o limite λ₁ é definido no item 15.8.2 “Dispensa da análise dos efeitos locais de 2ª ordem”).

O item 15.8.3 “Determinação dos efeitos locais de 2ª ordem” da NBR6118:2003 estabelece diversos métodos para análise local em 2ª ordem, cada qual com as suas limitações. Esquematicamente, tem-se:

IV.a. Métodos aproximados

O item 15.8.3.3 “Métodos aproximados” da NBR6118:2003 apresenta três opções possíveis para obtenção dos efeitos locais de 2ª ordem em pilares. São processos que possuem formulações diretas, e que portanto, possibilitam o cálculo manual.

A não-linearidade geométrica (NLG) nestes casos é sempre resolvida através do método do pilar-padrão, no qual a deformada do trecho de pilar é considerada de forma aproximada por uma senóide. O que varia entre os diferentes processos é o tratamento da não-linearidade física (NLF), ora pela curvatura aproximada, ora pela rigidez aproximada e ora pelo diagrama momento-curvatura.

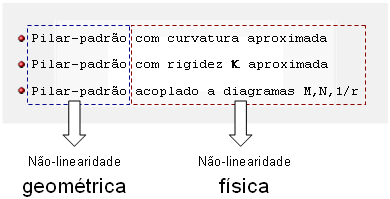
Tanto os métodos do pilar-padrão com curvatura aproximada e pilar-padrão com rigidez k aproximada, já foram adaptados aos sistemas TQS e estão em fase de testes.

IV.b. Método Geral

O Método Geral para análise dos efeitos locais em pilares, é descrito no item 15.8.3.2 “Método geral” da nova NBR6118:2003:

Pode-se afirmar que nesta única frase, resumem-se diversos conceitos que tornam o processo genérico e preciso, que no entanto, pode ser solucionado apenas com o auxílio de um computador.

Trata-se de um método obrigatório para λ > 140, mas que também pode ser utilizado para valores de índices de esbeltez inferiores.

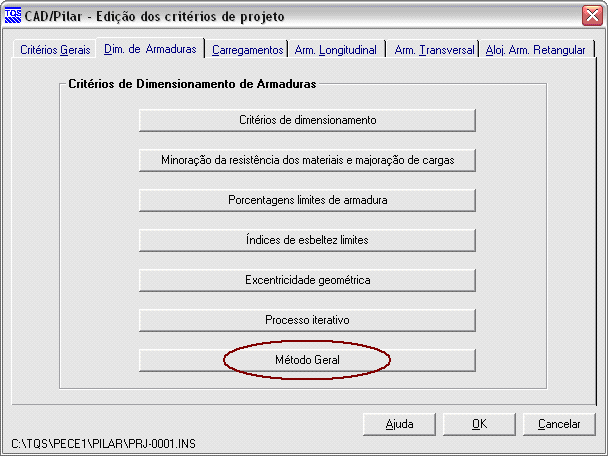
O Método Geral já foi adaptado nos sistemas TQS. Ele atende todas as condições estabelecidas pela nova norma descritas acima.

Maiores detalhes do Método Geral TQS, como: sua abrangência, filosofia de implantação nos programas, modelo utilizado, visualizador gráfico, etc, serão descritos nos capítulos seguintes.

V. O diagrama momento-curvatura

O concreto-armado possui um comportamento tipicamente não-linear. Basta recorrer aos diagramas tensão-deformação do concreto e do aço definidos na seção 8 “Propriedades dos materiais”, para que esta afirmação fique mais clara e evidente.

Além da aplicação direta destes diagramas para incluir o efeito da não-linearidade física nas análises, uma outra alternativa possível muito interessante é o uso das relações momento-curvatura, uma vez que os esforços é que são normalmente obtidos do processamento, e não as tensões.

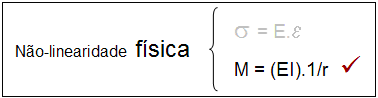
Através do diagrama momento-curvatura apresentado no item 15.3.1 “Relações momento-curvatura” da NBR6118:2003, é possível simular pilares submetidos à flexão composta oblíqua considerando o efeito da não-linearidade física de uma forma mais precisa.

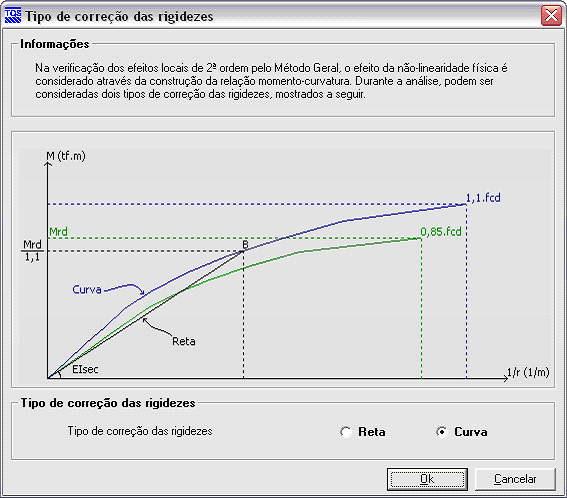
O Método Geral TQS monta o diagrama momento-curvatura real para cada uma das seções analisadas. Através de um critério, é possível adotar a correção das rigidez pela curva ou pela reta que define a rigidez secante EI_sec.

Utiliza-se a formulação de segurança permitida pela norma, na qual calcula-se os efeitos de 2ª ordem com ɣ_f/ɣ_f3, não esquecendo de majorar posteriormente com ɣ_f3, (ɣ_f3 = 1,1). Isto influencia diretamente na busca de uma posição de equilíbrio estável da estrutura.

Vale lembrar que o diagrama momento-curvatura varia em função das armaduras e da força normal atuante, ou seja, para cada lance de pilar tem-se um diagrama momento curvatura.

VI. Imperfeições locais

Todas as considerações sobre as imperfeições geométricas são apresentadas no item 11.3.3.4 “Imperfeições geométricas” da NBR6118:2003, cujo objetivo é determinar os efeitos ocasionados por distorções geométricas inerentes na execução de uma estrutura.

Na análise local, tanto o desaprumo de pilar, mas principalmente a sua falta de retilineidade, são condições que devem ser obrigatoriamente analisadas, pois não estão cobertas pelos coeficientes de ponderação.

Existem diferentes formas de considerar as imperfeições locais. Na antiga NBR6118:1980, isto era realizado através da adição de uma excentricidade acidental (ea). Já pela nova norma, isto pode ser feito através da verificação do momento mínimo de 1ª ordem. No item 11.3.3.4.3 “Momento mínimo”, descreve-se:

No Método Geral TQS, os efeitos das imperfeições locais serão simulados através da verificação do momento mínimo de 1ª ordem, ao longo de todo o lance do pilar.

VII. Flexão composta oblíqua

O item 15.8.3.3.5 “Método do pilar-padrão para pilares de seção retangular submetidos à flexão composta oblíqua” da NBR6118:2003, estabelece condições para seja realizada uma verificação local em pilares submetidos à flexão composta oblíqua, através de uma análise em que a interação entre as duas direções é levada em conta somente no final (análise desacoplada):

• λ < 90, nas duas direções.
• Rigidezes distintas para cada uma das direções.
• Seção retangular.
• Verificação se a composição dos esforços Mx e My finais estão dentro da envoltória resistente.

Através do Método Geral TQS, todas estas recomendações acima são atendidas e verificadas. Embora a rigidezes sejam tratadas de forma distinta para cada uma das direções, a interação entre os esforços Mx e My é verificada tanto durante a busca da posição de equilíbrio (modelo espacial), como na verificação final (envoltória real resistente).

VIII. Fluência

A consideração dos efeitos de fluência ou deformação lenta é obrigatória em pilares com λ > 90. Embora seja apresentada uma formulação no item 15.8.4 “Consideração da fluência”, uma outra opção mais interessante, que é calibrar o próprio diagrama tensão-deformação do concreto de modo a considerar os acréscimos de deformações ao longo do tempo, será utilizado no Método Geral TQS.

IX. Detalhes do Método Geral TQS

Através dos capítulos anteriores, foi possível notar que a nova norma NBR6118:2003 estabelece uma série de considerações que até então não eram tratadas pela antiga NBR6118:1980. São apresentados novos conceitos, novas formulações, bem como métodos mais precisos para análise dos efeitos locais em pilares.

Conforme já havia sido colocado, tanto os métodos aproximados como o Método Geral estão disponíveis nos sistemas TQS. Neste capítulo, serão apresentados detalhes do Método Geral TQS.

Apenas relembrando, o Método Geral é obrigatório para λ > 140, muito embora também possa ser utilizado para valores de índices de esbeltez menores.

IX.1 Abrangência

Através do Método Geral, será possível analisar os efeitos locais em pilares com as seguintes características:

• Seção qualquer
• Armadura simétrica ou não
• Submetidos à flexão composta normal ou oblíqua

IX.2 Filosofia da implantação nos sistemas

O Método Geral já foi incorporado no esquema de dimensionamento do TQS-Pilar. Em cada um dos lances de pilares existentes em um edifício, o programa automaticamente opta por um dos métodos aproximados ou pelo Método Geral, de acordo com o seu índice de esbeltez.

Através de um critério de projeto, é possível definir o índice de esbeltez limite que, uma vez ultrapassado, implicará na chamada do Método Geral, cujo processo de dimensionamento é realizado através de sucessivas verificações, já que a análise necessita das armaduras previamente definidas.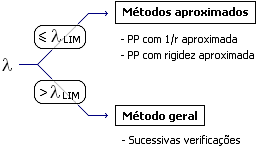

Além disso, foi adicionado um novo comando no Editor de geometria, esforços e armaduras em pilares, que possibilita de maneira extremamente rápida e simples analisar os efeitos locais em qualquer lance de pilar do edifício através do Método Geral.

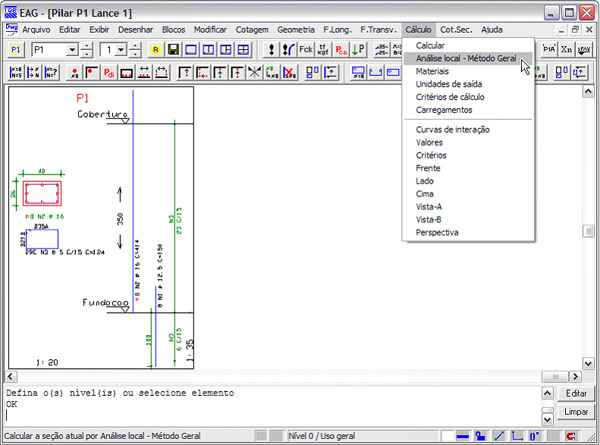
IX.3 Visualizador

Um visualizador 100% gráfico foi desenvolvido exclusivamente para análise dos resultados obtidos pelo Método Geral. Todas as informações relevantes podem ser visualizadas: resultados a cada iteração, diagramas momento-curvatura, dados da discretização do modelo local, restrições consideradas no topo e na base, etc.

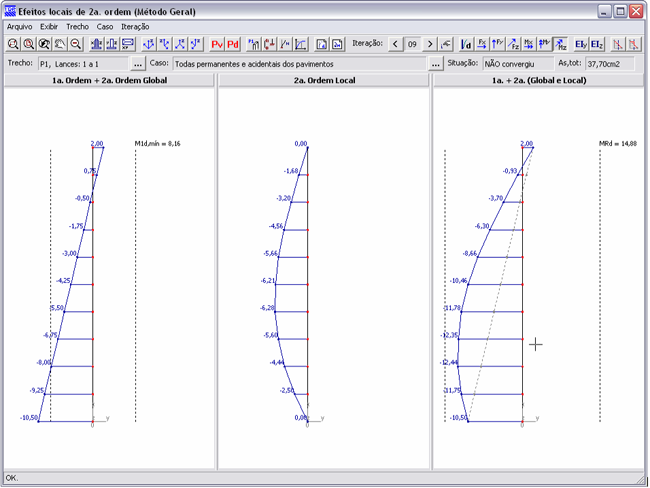
Sua tela principal é subdividida em três partes:

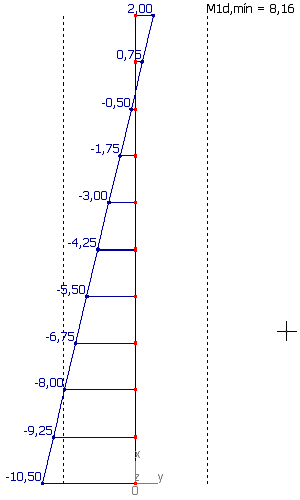
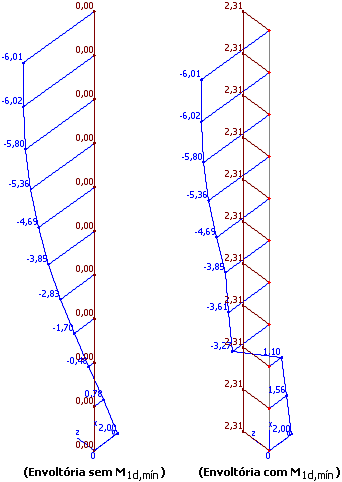
• No painel esquerdo, são visualizados os efeitos de 1ª ordem, acrescidos dos efeitos de 2ª ordem global. O limite referente ao momento mínimo de 1ª ordem (M_1d,mín) é mostrado por uma linha tracejada.
• No painel central, são mostrados os efeitos locais de 2ª ordem.
• No painel direito, são visualizados os efeitos totais (1ª ordem + 2ª ordem global + 2ª ordem local). O limite referente ao momento resistente último (M_rd) é mostrado por uma linha tracejada.

Os resultados podem ser analisados a cada iteração, desde a posição inicial até a posição final de equilíbrio. São mostrados diagramas de: deslocamentos, forças cortantes (Fy e Fz), força normal (Fx), momentos fletores (My e Mz), momento torçor (Mx), rigidezes (EIy e EIz), bem como as envoltórias de momentos (com e sem a consideração das imperfeições locais).

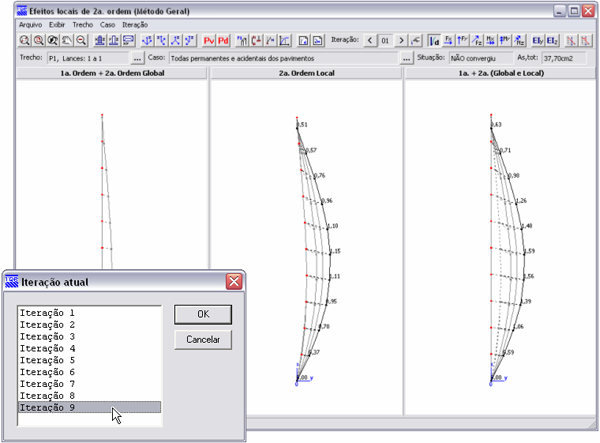
IX.4 Convergência

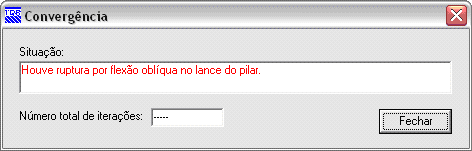
IX.5 Modelo

O lance de pilar analisado pelo Método Geral é simulado por um modelo espacial, montado a partir dos resultados do processamento do pórtico espacial do edifício. Trata-se de um trecho do pilar extraído do edifício.

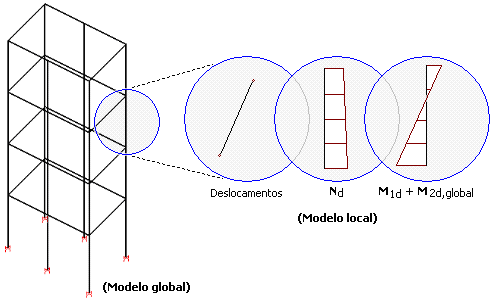
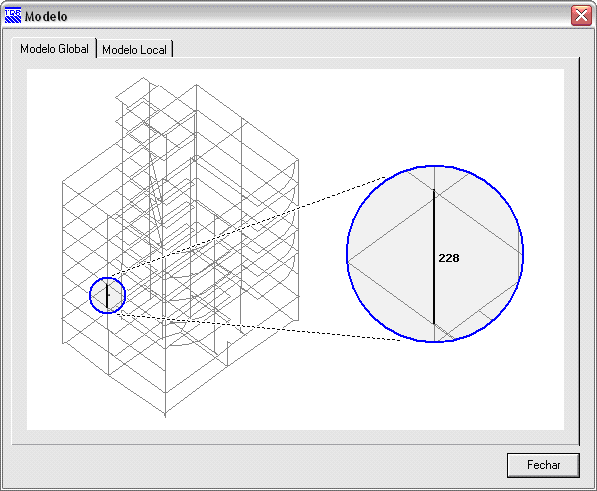
IX.5.a Discretização

Uma vez retirado do modelo global do edifício, o lance do pilar é discretizado de forma adequada.

Como o processamento do pórtico global do edifício somente fornece os deslocamentos nodais, isto é, no topo e na base do lance, torna-se necessário calcular a sua posição deformada inicial.

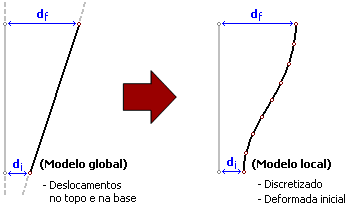
A discretização do modelo local é controlada por um critério de projeto.

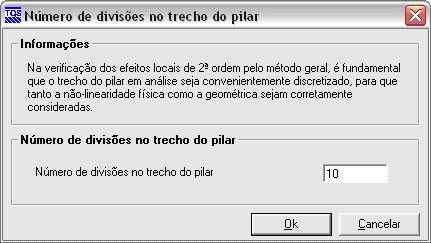
IX.5.b Vinculações

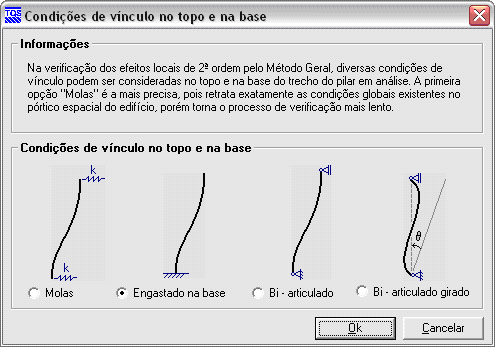
Através de um critério de projeto, as condições de vínculo no topo e na base dos lances podem ser consideradas de diferentes formas.

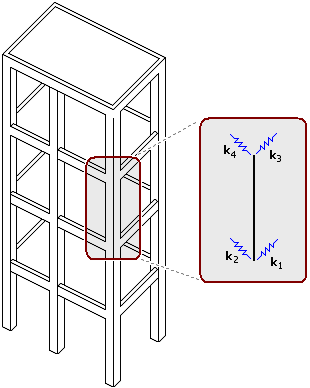
O modelo bi-articulado é a mais usual. Porém, uma das grandes novidades do Método Geral é a possibilidade do cálculo de molas no topo e na base, de tal forma que o modelo local retrate exatamente as condições de vínculo que os extremos do trecho do pilar estão submetidos no interior do edifício.

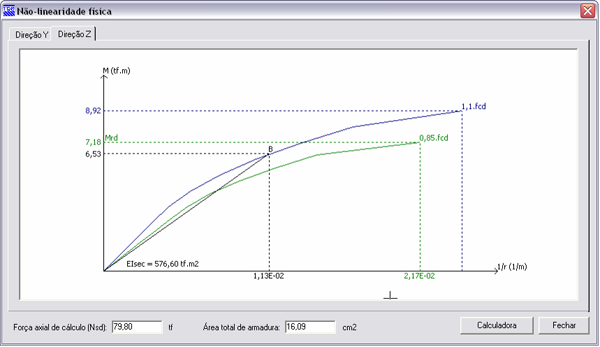
IX.6 Não-linearidade física (NLF)

A não-linearidade física é considerada através da aplicação direta do diagrama momento-curvatura. Através do visualizador, é possível verificar qual o diagrama utilizado na análise em cada uma das direções.

IX.7 Não-linearidade geométrica (NLG)

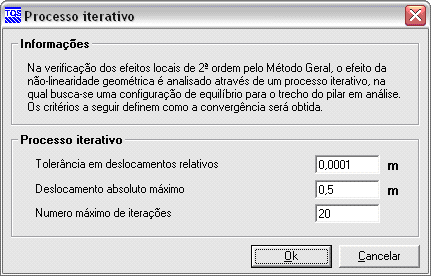
A não-linearidade geométrica é considerada através de um processo no qual busca-se uma configuração de equilíbrio estável através de sucessivas iterações.

Através de critérios de projeto, é possível definir como a convergência deve ser obtida.

IX.8 Flexão composta oblíqua

Por se tratar de um modelo local espacial, a interação entre os momentos solicitantes nas duas direções automaticamente é considerada durante toda a análise. Após o estabelecimento do equilíbrio, é feita a verificação se a composição dos esforços finais (N, My e Mz) ao longo de todo o lance está dentro da envoltória resistente.

Isto é realizado para duas situações:

• a. Envoltória SEM a consideração dos momentos mínimos de 1ª ordem
• b. Envoltória COM a consideração do momentos mínimos de 1ª ordem

X. Exemplos

Neste capítulo, serão apresentados alguns resultados obtidos pelo Método Geral TQS.

X.1 Exemplo 1

Trata-se de um pilar engastado na base, conforme mostra a figura a seguir.

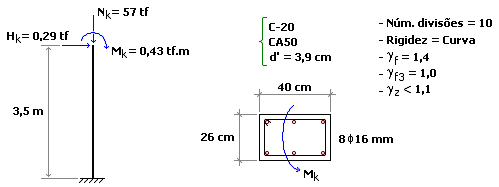
Embora não seja uma situação tão comum nas edificações de concreto-armado, este exemplo servirá para esclarecer certos conceitos interessantes. Os resultados obtidos pelo Método Geral TQS são apresentados a seguir.

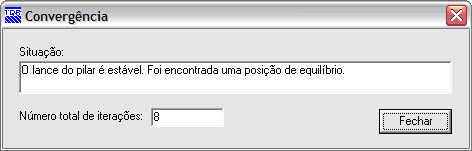
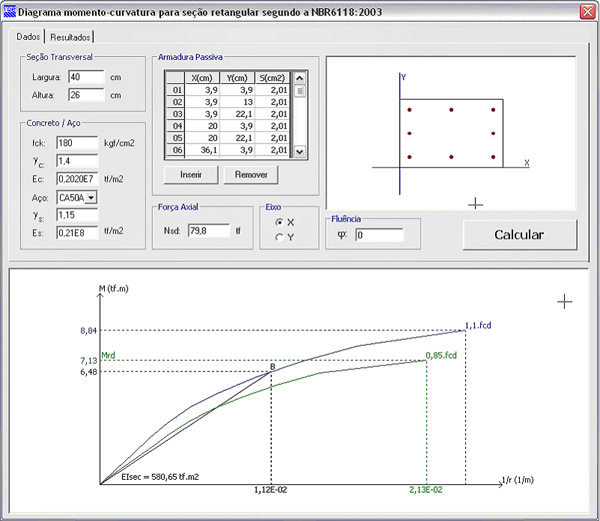
Diagrama momento-curvatura para a força normal N_d = 79,8 tf e armadura total de 16,09 cm²:

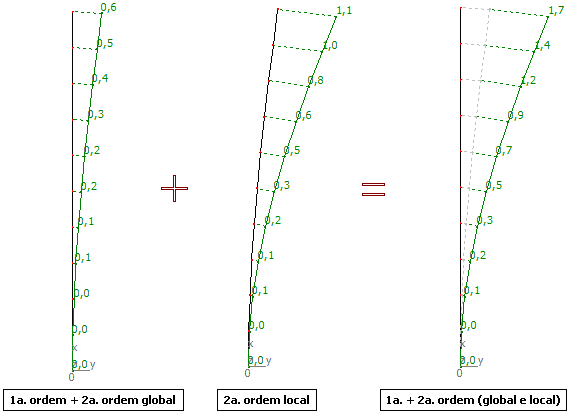
Momentos fletores na posição final de equilíbrio:

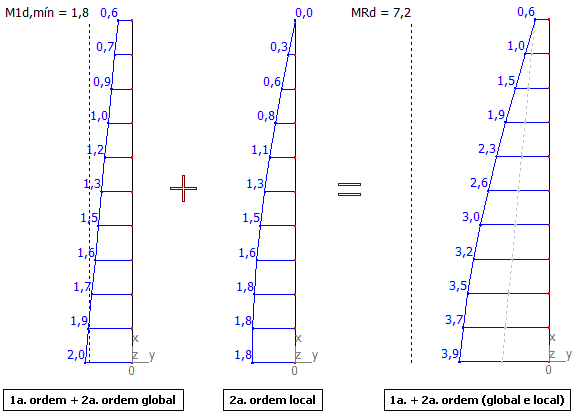
Os resultados anteriores foram obtidos utilizando-se a curva (1,1.f_cd) do diagrama momento-curvatura. Vamos agora, analisar o mesmo problema, porém através da reta que define a rigidez secante EI_sec, constante ao longo de todo o pilar.

Deslocamentos na posição final de equilíbrio:

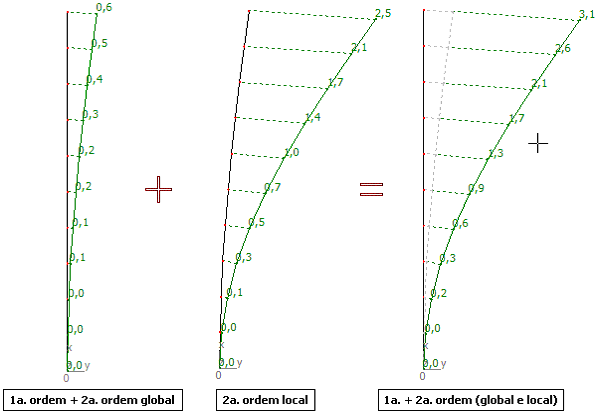
Momentos fletores na posição final de equilíbrio:

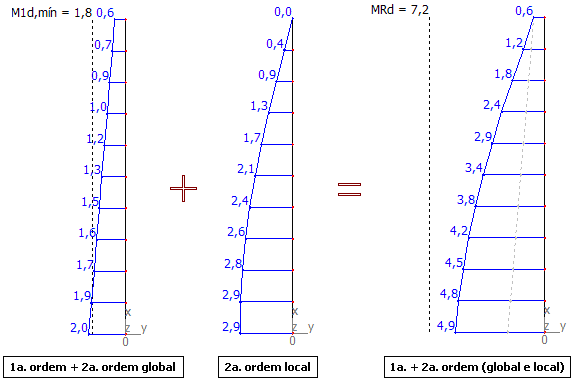
Nota-se que os resultados foram bem diferentes. Isto é claramente explicado através do diagrama momento-curvatura montado para o pilar analisado. A rigidez obtida pela reta secante para o nível de solicitações atuantes (0,6tf.m à 4,9 tf.m) é bem inferior ao da curva, conforme indica a figura a seguir.

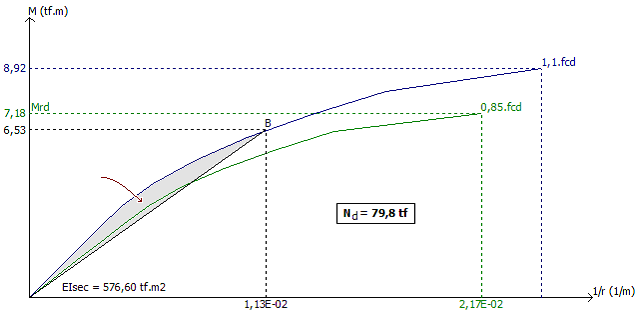
Rigidezes pela curva e pela reta:

Vale lembrar mais uma vez, que o diagrama momento-curvatura varia sensivelmente em função da normal de compressão e da configuração das armaduras dispostas na seção. Veja a seguir o diagrama para o mesmo pilar, porém com um força N_d = 120 tf. Praticamente, a diferença entre a reta e a curva deixa de existir.

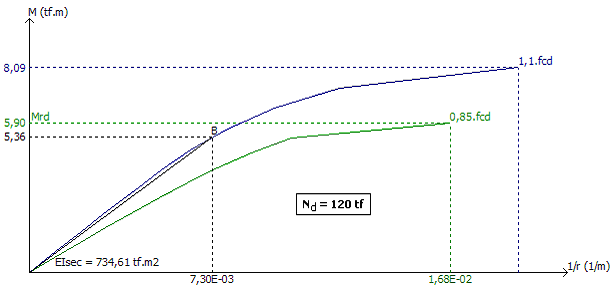
X.2 Exemplo 2

Trata-se de um lance de pilar submetido a uma flexão composta oblíqua, conforme mostra a figura a seguir.

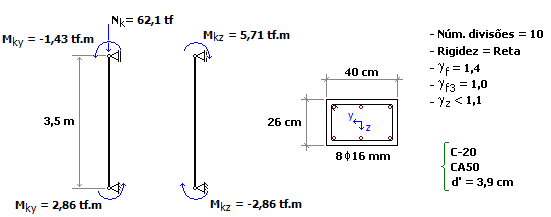
Os resultados obtidos pelo Método Geral são apresentados a seguir.

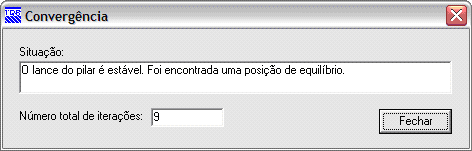
Diagrama momento-curvatura em z para a força normal N_d = 86,9 tf e armadura total de 16,09 cm²:

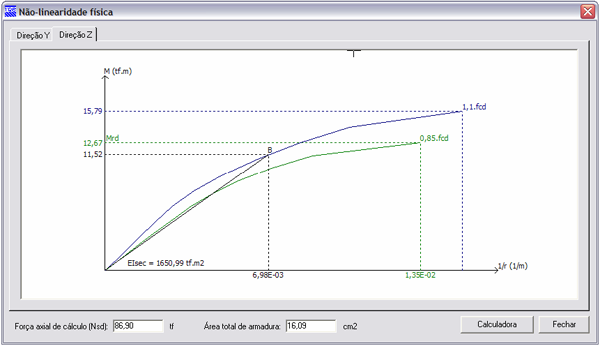
Diagrama momento-curvatura em y para a força normal N_d = 86,9 tf e armadura total de 16,09 cm²:

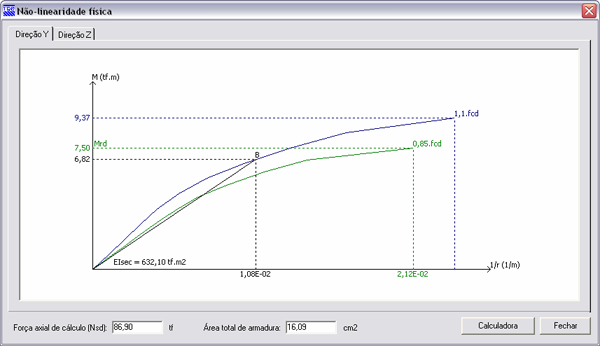
Deslocamentos na posição final de equilíbrio:

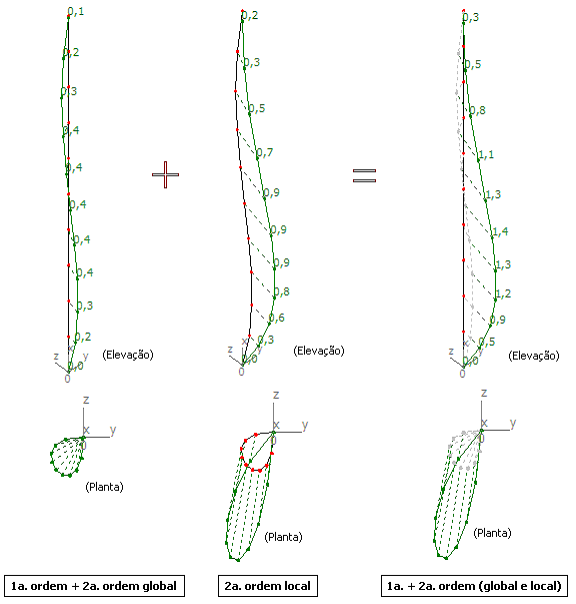
Momentos fletores My na posição final de equilíbrio:

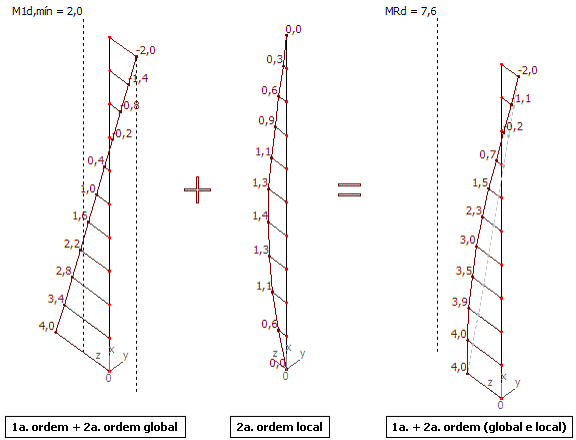
Momentos fletores Mz na posição final de equilíbrio:

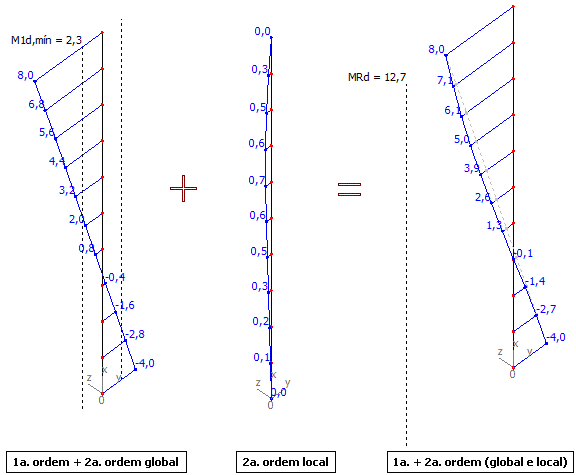
Envoltórias com e sem a consideração dos momentos mínimos de 1ª ordem:

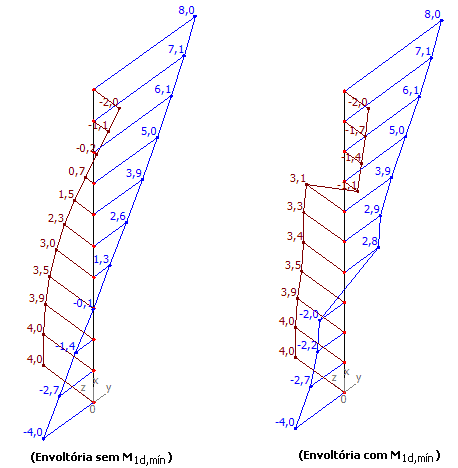
X.3 Exemplo 3

Trata-se de um lance de pilar submetido a uma flexão composta normal, conforme mostra a figura a seguir.

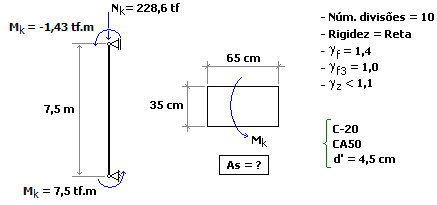
Os resultados obtidos não serão apresentados com detalhes como nos exemplos anteriores. O objetivo será apenas de comparar o dimensionamento obtido pelo Método Geral com os processos aproximados existentes na nova norma.

As armaduras dimensionadas foram:

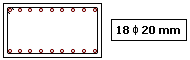
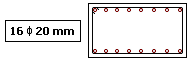
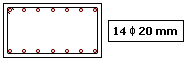
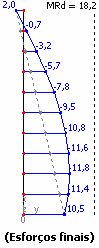
XI. Comentários finais

Através dos capítulos anteriores, foi possível apresentar de maneira resumida alguns dos diversos conceitos estabelecidos pela nova NBR6118:2003. Foi demonstrado também como eles são adaptados nos sistemas TQS.

A grande novidade é a análise dos efeitos locais pelo Método Geral, na qual as não-linearidades física e geométrica serão tratadas de forma detalhada e 100% automatizadas.

XII. Referências

FRANÇA, R.L.S. Contribuição ao estudo dos efeitos de segunda ordem em pilares de concreto-armado. São Paulo, 1991. Tese (Doutorado)

FRANÇA, R.L.S. Relações momento-curvatura em peças de concreto-armado submetidas a flexão oblíqua composta. São Paulo, 1984. Dissertação (Mestrado)

SANTOS, L.M. Estado limite último de instabilidade, EP/USP, São Paulo, 1987.

PECE/USP "Estabilidade global e análise de peças esbeltas", Notas de aula, 2003.

ABNT NBR6118:2003 “Projeto de estruturas de concreto – Procedimento”, 2003.