Casos Especiais de Protensão

Generalidades

A protensão tal como vem sendo usada em obras de rotina já está bem compreendida por todos e não constitui matéria para ser abordada neste curso. Entretanto casos particulares que fogem à intuição ou que exigiriam alguma reflexão mais profunda podem ser interessantes pois aguçam a sensibilidade e permitem melhor do que os casos usuais, fixar os conceitos.

A melhor maneira de entender bem o conceito de protensão é procurar afastar a matemática, que só deve ser aplicada depois que os conceitos tiverem sido muito bem absorvidos.

A protensão deforma as peças. Sem deformação não há protensão. Quando existirem várias peças juntas, a protensão se reparte entre elas de acôrdo com as respectivas rigidezes.

Sabe-se que a rigidez das peças comprimidas é geralmente muito maior do que a rigidez das peças fletidas. A protensão pode ser aplicada comprimindo axialmente a peça (fig. 1) ou fletindo-a (fig. 2). A deformação no primeiro caso é de um encurtamento. No segundo, de um encurvamento.

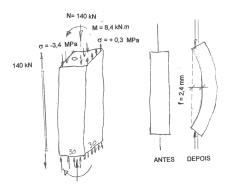
Fig. 1 – Protensão por compressão centrada

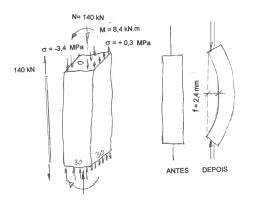
Fig. 2 - Protensão por compressão excêntrica (flexo-compressão)

Coloquemos alguns valores, para que se tenha uma idéia melhor. Seja uma barra de seção quadrada 30 x 30 cm e comprimento L=6 m. No caso da Fig. 1 a barra possui um furo centrado por onde pode passar um cabo de aço (cordoalha) de ? 12,7 mm ao qual se pode aplicar uma força de 140 kN. A tensão no concreto será ?_c = -0,140 / 0,302 = -1,5 MPa (compressão: negativa). Para um módulo de elasticidade Ec = 23.500 MPa (correspondente a uma resistência f_ck = 25 MPa) a deformação longitudinal da peça será em radianos e_c = -1,5 / 23.500 = -0,064 ‰ (ou seja mm/m). O deslocamento de uma das seções extremas em relação à outra é então ?L = -0,064 x 6 ? -0,4 mm, o sinal indicando que se trata de uma aproximação das extremidades (encurtamento da peça). Percebe-se que o deslocamento é muito pequeno! Esse deslocamento poderia tambem ser calculado por NL /E_c.A_c = 0,140 x 6 / 2.115 = 0,0004 m = 0,4 mm, sendo o produto no denominador a rigidez por compressão E_c.A_c = 23.500 x 0,09 = 2.115 MN.

No caso da Fig. 2 o furo é excêntrico. Para maior simplicidade, imaginemos que o furo é reto, paralelo ao eixo da peça, com excentricidade e = 6 cm. Suponhamos que o cabo seja idêntico ao do caso anterior, com a força aplicada de 140 kN. As tensões numa seção transversal qualquer, não importa qual seja, pois a excêntricidade do cabo é constante, são facilmente determinadas e valem -3,4 MPa (compressão: negativa) na borda mais próxima do cabo e +0,3 MPa na borda oposta. Essas tensões são provocadas por uma força normal N = 140 kN e por um momento M = 140 x 0,06 = 8,4 kN.m. A deformada da peça é uma curva representada pelo eixo, inicialmente reto, que se deformou. O afastamento máximo do eixo deformado ocorre no meio da peça e se denomina "flecha". Essa flecha calculada em regime elástico, com o concreto resistindo à tração de 0,3 MPa vale 2,4 mm.Essa flecha é calculada com a rigidez por flexão E_cJ_c = 15,86 MN.m² resultando um deslocamento muito maior do que o provocado pela compressão centrada de 0,4 mm que continúa existindo concomitantemente com a flecha. Ao mesmo tempo que a peça se encurva, aparece tambem o encurtamento longitudinal de 0,4 mm sem contar o efeito de 2ª ordem devido à diminuição da corda com o encurvamento.

Se a força de 140 kN for aplicada simultaneamente a uma peça metálica que envolve a de concreto e a ela esteja aderente, dependendo das rigidezes relativas E.A, pode acontecer de o concreto não receber sinão uma parcela insignificante da protensão. Isto tem sido um erro bastante freqüênte em projetos mal quantificados. Imagine-se um tubo de aço de seção quadrada com chapa soldada de espessura 12,5 mm, dentro do qual tenha sido moldada a peça da Fig. 1. A seção de concreto é 900 cm² e sua rigidez, como já mencionado, é E_cA_c = 2115 MN. O tubo de aço possui seção de 150 cm² e uma rigidez E_sA_s = 210.000 x 0,0150 = 3.150 MN. Considerando a rigidez total do concreto e do aço 2.115 + 3.150 = 5.265 MN, verifica-se que a rigidez do tubo de aço contribui com 60% do total e portanto, da força de protensão aplicada de 140 kN apenas 40% vai efetivamente protender o concreto. Se o concreto sozinho é comprimido com a tensão de 1,5 MPa, no caso do concreto dentro do tubo de aço ele só receberá a compressão de 0,4 x 1,5 = 0,6 MPa, menos da metade do valor previsto.

Quando numa obra se aplica a protensão em cabos embutidos numa laje que, para receber a protensão prevista deve arrastar pilares para que os deslocamentos se realizem, pode acontecer que os pilares venham a receber uma fração significativa da protensão. Vejamos um exemplo: uma laje de 16 cm de espessura e um vão de 8 m, possui numa faixa de 2 m de largura, cabos engraxados de ? 12,7 mm espaçados de 20 cm. A protensão resultante na faixa é de 10 x 140 = 1400 kN. Existem nas extremidades pilares de 20 x 150 cm com a dimensão de 150 cm na direção do vão. As rigidezes são, para concreto com fck = 25 MPa:

Da laje 23.500 x 0,16 x 2,00 = 7520 MN

Dos pilares 23.500 x 0,20 x 1,5³/12 = 1.321 MN.m²

Não é possível comparar diretamente as rigidezes pois são de natureza diferente, mas mesmo assim já servem para que se tenha uma idéia dos valores, mostrando que a laje se deformando por compressão simples parece ser mais rígida do que os pilares se deformando por flexão. Entremos um pouco mais a fundo nos deslocamentos.

Deslocamento relativo da extremidade da laje em relação ao centro: ?L = 1,400 x 4 / 7520 = 0,7 mm

Deslocamento por flexão do pilar com 2,5 m de altura: f = 1,400 x 2,5³ / 8 x 1.321 = 2,1 mm

Estes valores ?L e f são comparáveis, pois estão na mesma unidade. Notase que o deslocamento da laje representa apenas a quarta parte do total ?L + f . Assim sendo, a laje absorverá A MAIOR PARTE DA PROTENSÃO, PORQUE É MAIS RÍGIDA. A protensão será distribuida pelas peças na relação inversa dos valores 0,7 e 2,1 mm. Quem apresentar menor deslocabilidade receberá o maior quinhão. A protensão será repartida entre laje e pilares na seguinte proporção 1/0,7 para a laje e 1/ 2,1 para os pilares ou seja, 75% para a laje e 25% para os pilares. Vê-se portanto que os pilares recebem uma parcela significativa da protensão. Se não refletirmos seriamente sobre este problema, pensaremos que a laje estará recebendo toda a protensão, quando na realidade receberá apenas ¾ do que se pretende. Lembrando que, no decorrer do tempo haverá uma perda de mais ou menos 20% por fluência e relaxação, restará na laje apenas 0,75 x (1 - 0,20) = 60%! Isto não pode deixar de ser pensado. Quantos projetistas pensam neste problema?

É por isso que se observam trincas importantes em lajes protendidas, em serviço! Isto é bastante agravado quando se aplica a protensão prematuramente, por exemplo aos 3 dias. Pensa-se que, se a resistência do concreto é suficiente para manter os fios esticados sem haver escorregamento (diretamente ligado à resistência à tração do concreto), a protensão pode ser realizada sem transtornos. Acontece que os pilares já possuem maturidade bem maior do que a laje e portanto seu módulo de elasticidade já cresceu. A laje aos 3 dias, ainda não possui um módulo de elasticidade pois ele ainda "está nascendo"! A rigidez dos pilares é maior ainda do que nos cálculos acima, quando os módulos de elasticidade são iguais para laje e pilares. Imagine-se que o módulo da laje não ultrapasse 50% do dos pilares. Isto significa que o deslocamento da laje ao invés de ser 0,7 mm será 0,7/0,50 = 1,4 mm. A participação no deslocamento relativo total é então 1,4 / (1,4 + 2,1) = 0,40. A laje receberá então a fração de 60% e não 75% como se pensava. No decorrer do tempo este valor cairá para 0,60x(1-0,20) = 48%, isto é, apenas a metade do que foi calculado!

A fissuração do concreto surge como um corretivo da natureza para estes cochilos dos projetistas ou dos construtores.

As razões para que se esperem pelo menos 10 dias para a aplicação da primeira parcela da protensão são portanto muito importantes e muito difíceis de convencer os construtores que só estão interessados em cumprimentos de prazos e em aproveitamento de fôrmas... Por causa de uma semana ficamos com a obra condenada para o resto da vida. Não existem mais desastres por causa da elevada segurança com que se projeta.

O que se disse aplica-se a qualquer tipo de obra. O interesse no momento é a aplicação da protensão a casos especiais que pretendemos ilustrar com exemplos reais extraidos de nossa vida profissional.

Primeiro Exemplo: Cobertura do túnel Rebouças no Rio

Este caso, que ocorreu na década de 60, foi objeto de uma concorrência. A idéia era executar rapidamente uma casca cilíndrica com raio de curvatura maior do que o do túnel, separando um volume de ar entre a cobertura e a rocha cortada. A casca de concreto serviria ao mesmo tempo de acabamento do teto do túnel e de condutos de ar, separando o ar poluido sugado e o ar puro injetado. A casca seria constituida de lâminas cilíndricas de largura da ordem de 2 m (para possibilitar um transporte fácil pelas rodovias) e de espessura de 5 cm, para vencer vãos da ordem de 12 m. A casca seria levantada por 4 pontos, por meio de um balancim de 5 m que receberia os 4 cabos inclinados presos em ganchos salientes na própria casca, ficando balanços de apenas 2,5 m (?0,207.L). Foi estudada a altura disponível para a grua móvel penetrar no túnel e montar a peça em consolos contínuos, inclinados previamente preparados para servirem de apoio às cascas. O limite de peso para os equipamentos disponíveis na época para a montagem era de 40 kN e cada peça pesava cerca de 39 kN.

A peça era levantada com o balancim ligeiramente excêntrico, resultando uma subida oblíqua, de tal modo que as extremidades da peça conseguissem passar entre os consolos já executados. Tendo passado no vão livre de 11,8 m a casca descia suavemente até que sua extremidade mais baixa se apoiasse num dos consolos corridos, onde existiriam placas de neoprene já colocadas em posições corretas. Continuando a descer, a casca só poderia descer do outro lado, até que encostasse nos correspondentes aparelhos de apoio de neoprene. Depois de instalada a peça, o gancho do balancim era deslocado para a posição simétrica e a peça era novamente levantada para o posicionamento final e o encostamento na peça vizinha, anteriormente instalada.

As juntas laterais eram grautedas, preenchendo a cunha escavada nos extremos da peça pré-fabricada, exatamente como acontece com os painéis alveolares tão comuns em nosso meio. Resultava uma junta estanque, sem degraus com possibilidade de um trabalho em conjunto. Eventuais pequenos degraus, que sempre aparecem nas execuções mais cuidadosas por diferenças de comportamento elástico das peças (principalmente por diferenças de temperatura durante a cura térmica), poderiam ser compensadas por engenhoso aperto com pequenos T de aço encaixados entre as peças e apertados pela parte superior com parafusos soldados. Como era a protensão de tais peças, tão finas, com apenas 5 cm de espessura?

As peças foram concebidas com protensão centrada, num molde curvo de aço, com bordas com o perfil de forma bem estudada e extremidades perpendiculares à superfície média da casca (Fig. 3). Os fios de protensão acompanhavam a curvatura da peça e eram apoiados em roletes constituidos por tubos metálicos ôcos de parede fina e diâmetro interno de 12,7mm cheios com argamassa. Os roletes tinham a finalidade de permitir que os fios de aço de protensão, que eram de aço CP150 com diâmetro ? 5 mm, acompanhassem a curvatura da peça com disposição simétrica.

Cada fio era protendido com a força de 20 kN e era preso com cunhas nas extremidades da "mesa de protensão", que possuia resistência suficiente para resistir à força dos 40 fios esticados um por um. Os fios, dispostos em uma só camada central eram esticados por uma das extremidades escorregando sobre roletes, sendo nessa operação alongados de 76 mm. Após o esticamento controlado com precisão de milímetro, os fios eram presos por meio de cunhas provisórias recuperáveis, situadas em vigas extremas de aço, sobre calços de 100 mm que poderiam ser retirados na hora da transferência da protensão da "mesa" para a peça.

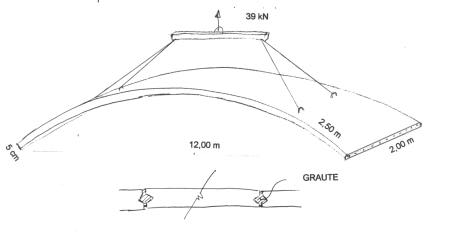
Fig.3 - Elemento pré-fabricado para cobertura do túnel Rebouças (projeto)

A situação crítica para a peça da Fig. 3 era a situação de montagem. A peça seria fabricada com f_ck = 30 MPa e seria protendida quando a tensão alcançasse o valor f_cj = 21 MPa.

A Fig. 3 mostra o carregamento no instante de montagem, com balanço de 2,5 m e carga de peso próprio (M_g = 7,82 kN.m).

A verificação seria feita no Est. Ib com o concreto da zona superior (tracionada) com módulo de elasticidade igual a 1/3 do módulo da zona comprimida, levando em consideração a plastificação do concreto tracionado. A dedução das expressões que levam em conta módulos diferentes não interessa aqui.

Considerando a protensão sem perdas (pois as peças seriam fornecidas na obra imediatamente após a fabricação) os cálculos a seguir mostram alguns valores. A tensão inicial de protensão era ?_pi = 1000 MPa e a área da seção ideal com E_c = 4700.?21 = 21.500 MPa e E_s = 210.000 MPa vale A_i = 1070 cm² resultando a tensão inicial de protensão centrada no concreto:

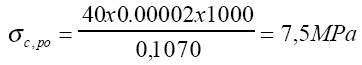
e a tensão correspondente no aço

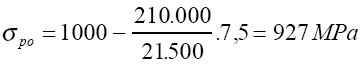
Na montagem, os esforços solicitantes eram apenas o momento de peso próprio g = 2,00x0,05x25 = 2,5 kN/m no balanço de 2,5 m acrescido de 20% de impacto:

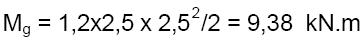
A força de protensão aplicada ao concreto após a liberação da peça protendida era N_po = 927 x 40 x 0,00002 x 1000 = 742 kN.

Sob a ação dos esforços M_g e N_po o cálculo da peça de concreto simples no Est. Ib fornece as tensões nas bordas superior e inferior nas seções onde estão os ganchos de levantamento:

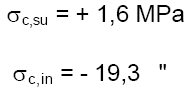
A tensão de 19,3 MPa de compressão no concreto representa apenas 64% do valor especificado de f_ck na data, sendo portanto satisfatória segundo a norma de prémoldados. A tensão de tração de 1,6 MPa mostra que a peça pode resistir sem fissurar. Cálculo adicional no ELU mostra que a área de aço de protensão necessária é de 3,4 cm2, existindo 8 cm² existindo portanto segurança 2,4 vezes maior do que a exigida em normas.

Depois de montada a obra, as tensões são uniformes em todas as seções, com o valor final (20% de perdas progressivas) de 3,2 MPa, valor bastante folgado. Por razões políticas a obra não foi executada conforme o projeto apresentado, bem mais econômico do que a execução tradicional final que se pode apreciar no túnel em funcionamento.

Outro exemplo de aplicação de protensão centrada é extraido do livro de Möll - Hormigón Pretensado (Fig. 4 [1]). Trata-se de uma escada helicoidal executada com elementos pré-moldados, com 20 cm de altura em cada degrau e largura de 120 cm, vencendo um desnível de 4 m. A espessura da laje é 12 cm atravessada por 3 furos de ? 3,5 cm para passagem de 3 cabos de protensão constituidos cada um, de 12 fios paralelos de 5 mm. A fig. 5 mostra uma seção longitudinal desenvolvida pelo eixo da escada mostrando a posição dos 3 cabos ancorados nos extremos dos degraus 1 e 19. Os fios não são cortados rentes à ancoragem mas se prolongam e penetram, na parte inferior num bloco de 55 x 40 x 120 cm que serve de apoio à base da escada, na parte superior numa viga de seção retangular 70 x 35 cm, possuindo um encosto inclinado para apoio do degrau 19. O bloco da base é previamente concretado com as extremidades dos 3 cabos além das ancoragens inferiores pré-cravadas, imersas no concreto. O degrau 1 é diferente dos demais pois possui um nicho para alojamento das ancoragens e um formato apropriado para encaixe no bloco como se vê na fig. 5.

Fig. 4 - Escada helicoidal com degraus pré-moldados (Möll - [1])

Ele é enfiado nos 3 cabos que saem do bloco e se encosta no encaixe através de uma manta asfaltica que evita a aderencia. Dessa forma o apoio inferior da escada no bloco é articulado. Os degraus sucessivos são enfiados nos cabos um por um e suportados por um cimbramento apropriado. Depois de montados os 19 degraus, os 3 cabos são protendidos com 20 toneladas cada um e suas pontas salientes são distribuidas dentro da fôrma da viga quando terminada a cravação das cunhas. A viga, que constitui o degrau 20 e encosta totalmente no degrau 19, fica solidarizada com a escada por meio dos cabos salientes. Qualquer movimentação da escada, por efeitos térmicos, por cargas de uso ou por efeitos reológicos do concreto, não causa esforços de coação prejudiciais ao bom funcionamento da escada, cujo peso próprio se distribui sem hiperestaticidade pelos dois apoios. Na Fig. 5 vê-se ainda um desgrau isolado em perspectiva, com indicação dos 3 cabos de protensão e as medidas principais. Pelo efeito de perspectiva as larguras de 120 cm dos degraus ficaram muito reduzidas para que se pudesse perceber que as extremidades por onde passam os cabos, são retângulos reversos e os próprios cabos seguem uma hélice diferente por causa da variação do raio em planta.

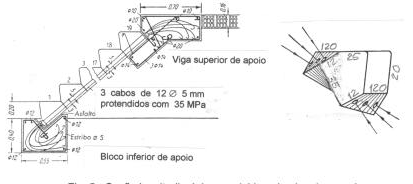
Fig. 5 - Seção longitudinal desenvolvida pelo eixo da escada helicoidal da Fig. 4. No detalhe um dos degraus em perspectiva, mostrando as posições dos 3 cabos [1].

Para ilustrar melhor o fato de que na protensão centrada não havendo flexão as deformações são exclusivamente axiais e portanto muito menores do que as deformações por flexão ( ou por torção) como se viu nas Figs. 1 e 2, foi construido um modelo de escada helicoidal (Fig. 6). Neste modelo, usou-se um tubo fino de cobre, dentro do qual passava um cabinho de ? 3 mm. Este cabinho foi esticado mediante um sistema de porca e parafuso, acionado com a mão, ficando a extremidade inferior fixa. Para tornar mais vizível o efeito, foi desfeita a fixação inferior e o cabinho foi introduzido num furo feito numa barra roliça de madeira dura e ancorado. Dois homens, um de cada lado, forçaram a barra de madeira para baixo e, enquanto isto se observava a extremidade superior. Esta permanecia praticamente fixa, sendo o deslocamento devido apenas ao encurtamento do tubo de cobre ao longo de seu desenvolvimento, igual ao encurtamento do tubo retificado e submetido à mesma força. Aplicando entretanto com a mão uma pequena força externa na parte superior, a deformação foi enorme. Predominavam os deslocamentos devidos à flexão e à torção, os únicos perceptíveis a olho. Tal modelo mostrava melhor do que palavras que a protensão aplicada por dentro do tubo só produz reação axial em cada seção transversal do tubo. Não importando o formato do eixo do tubo, a protensão assim aplicada só produz esforços axiais. O efeito dos demais carregamentos é calculado de maneira independente da protensão.

Fig. 6 - Modelo de escada helicoidal sendo submetido a uma protensão axial por meio de dois homens que fazem a função de macaco.

Segundo Exemplo: Protensão por aquecimento

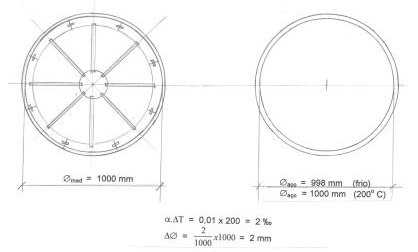
Fig. 7 - Protensão aplicada por meio de calor, ao aro de uma carroça.

Todo mundo sabe que, desde épocas imemoriais, os aros das rodas de carroças são montados a quente. Para uma roda constituida de peças isoladas de madeira que se encaixam entre si e nos raios que partem de uma peça central chamada "cubo", com diâmetro externo de 1000 mm é previsto um aro de aço com 998 mm de diâmetro interno a frio. Não há possibilidade deencaixar a roda de madeira dentro do aro. Porém, aquecendo o aro a 200º C, com o coeficiente de dilatação do aço de 0,01 mm/m o aumento de diâmetro será igual a 2 mm, sendo possível então encaixar a roda de madeira. Colocado o aro na posição certa, imediatamente ele é resfriado para não queimar a madeira e, não podendo encurtar, ficará submetido a uma pressão interna suficientemente grande para produzir um atrito que impeça sua extração. Se a madeira não cedesse absolutamente nada, o aro ficaria sujeito a uma tração correspondente à deformação de 2‰ e a tensão correspondente seria igual à tensão de escoamento do aço. Como a madeira sempre cede algo, a tensão se torna um pouco menor. A fig. 6 mostra o que se explicou com palavras.

Quando um material é aquecido ele sofre um aumento de comprimento caracterizado pelo coeficiente de dilatação ? rad/ºC. Para o aço este coeficiente vale ? = 10-5 rad /ºC= 0,01 mm/m/ºC. Se uma haste de aço sofre um aumento de temperatura, ela se alonga de

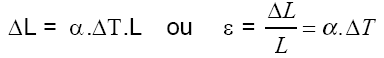
Para um aumento de temperatura ?T = 150 ºC o alongamento específico de uma haste de aço será

? = ?.?T = 0,01 x 150 = 1,5 mm / m

Prendendo-se a haste aquecida de tal maneira que ela não possa se encurtar ao esfriar, aparece uma tensão de coação determinada pela lei de Hooke: ?_s = ?.E_s

Sendo E_s = 210.000 MPa o módulo de elasticidade do aço, a tensão que surge para anular o encurtamento é de tração e vale

?_s = 1,5 x 10^-3 x 210.000 = 315 MPa

A aplicação da lei de Hooke exige neste caso que o material possua um limite de escoamento f_y > 315 MPa. Se o aço for CA-25 cujo limite de escoamento é f_y = 250 MPa não é necessário esquenta-lo até 150 ºC bastando adotar ?T = 119 ºC pois

? = ?.?T = 0,01 x 150 = 1,5 mm / m

?_s = 1,19 x 10^-3 x 210.000 = 250 MPa

Se a haste tiver sido esquentada a mais do que 119 ºC sua dilatação será maior do que 1,19 mm / m e, para impedir seu encurtamento ao esfriar será necessário aplicar uma tensão que produza tal deformação, superior à de escoamento da haste. Ao ser atingido o escoamento, a deformação da haste se processa com tensão constante. Portanto, qualquer que seja a temperatura de aquecimento, superior a 119 ºC, a haste impedida de se encurtar apresentará uma tensão constante de coação de 250 MPa. Este é o princípio da protensão por aquecimento: a haste é aquecida a uma temperatura qualquer acima de 119 ºC e nessa temperatura a barra é bloqueada, por solda por exemplo. Ao esfriar ela vai apresentar uma tensão igual à de escoamento.

Para que isto aconteça é necessário que a deformação imposta não exceda a correspondente ao fim do escoamento, que para o aço doce é muito grande, acima de 10%. Dificilmente se conseguirá esquentar uma barra para se conseguir um alongamento de 10% o que daria uma variação de temperatura de 10.000 ºC e o aço já estaria derretido!

Note-se que todo este raciocínio independe do comprimento e da área da seção transversal da haste. A introdução do comprimento influiria apenas no alongamento total e a área, apenas na força, ficando tensão e deformação invariáveis. Fixado o valor de

? = ?.?T fica definida a tensão, independentemente do comprimento e da área da seção. A força é proporcional à tensão, que será sempre a tensão de escoamento, e à seção. Desejando-se aplicar forças maiores, a solução é aumentar a seção da haste. O comprimento da haste influirá apenas no valor da dilatação total. Uma haste curta, por exemplo 2,0 m fornecerá um alongamento total de 3 mm, por exemplo, ao passo que uma haste de 20 m terá para a mesma variação de temperatura, um alongamento de 30 mm. A tensão entretanto será a mesma e dependerá apenas de

?T.

Este modo de protender já foi aplicado em diversos casos patológicos, de estruturas que sofreram danos. É citado aqui o caso de uma viga de ponte rolante em uma indústria em funcionamento, que não podia sofrer paralizações.

A viga era pré-moldada em concreto armado, em forma de duplo T com variação brusca da espessura da alma. Um dia, sob carregamento excepcional, apareceu uma trinca inclinada de 45º assustadora, com quase meio milímetro de abertura. A verificação do projeto mostrou deficiência no dimensionamento dos estribos na região em que a espessura da alma ficava reduzida. Não existia a menor condição de substituir a viga, nem de criar um enchimento com novas armaduras.

A solução dada ao problema foi de fazer um cintamento por meio de chapas de aço A36 na região fissurada. Entre o trilho e a face superior da viga existia um espaço livre de 2,5 cm entre calços do trilho. Este espaço seria suficiente para passagem de uma chapa de 20 mm de espessura e largura de 15 cm, pois a distância entre calços era de 25 cm. Esta chapa ultrapassava cerca de 3 cm de cada lado, a largura da mesa de 25 cm da viga. A viga pré-moldada era suficientemente lisa na parte superior, de modo que não foi necessário intercalar nenhum elemento macio para distribuição de cargas. Chapas verticais de mesma largura e espessura de 16 mm, cortadas em bisel em ambas as extremidades, foram cortadas com comprimento igual à altura total da viga, como mostra o esquema da Fig. 8. Essas chapas foram soldadas na chapa superior de 20 mm, em ambos os lados, formando com ela uma peça em forma de U invertido, aberto em baixo. Na parte inferior foi posicionada uma chapa idêntica à de cima, presa somente com um chumbador de plástico e um parafuso, apenas para simplificar as operações subsequentes. As chapas laterais em bisel ficavam exatamente 2 mm acima da chapa inferior, valor garantido por meio de um calço provisório de 2 mm durante a operação de soldagem na parte superior. Retirado o calço, ficava um espaço vazio de 2 mm.

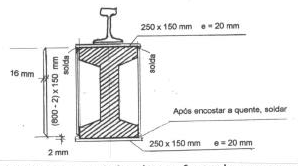
Fig. 8 - Seção transversal da viga reforçada com as chapas de reforço

Como os estribos existentes (CA-60) já deviam ter entrado em escoamento, foi prudente desconsidera-los totalmente. Os estribos existentes na extensão horizontal de 80 cm na região da trinca possuiam uma área de 4 cm² e os estribos necessários com a limitação das normas brasileiras ( com f_yd ? 435 MPa e concreto C30) seriam de seção 9 cm²/m. Como os estribos realmente aplicados eram de ? 6 mm CA- 60, a área necessária com f_yd = 600 / 1,15 = 522 seria 10,8 cm²/m. A força atuante nos estribos existentes no trecho de 80 cm abrangido pela trinca, supostos trabalhando no escoamento com 522 MPa seria de 560 kN. Cumpre aplicar uma protensão capaz de substituir esses estribos, suportando portanto a força de 560 kN. A Fig. 8 mostra o cintamento previsto com suas dimensões. Aquecidas as faixas laterais a 250 °C o alongamento dos 80 cm de seu comprimento inicial será 0,01 x 250 x 0,80 = 2 mm, preenchendo totalmente o espaço vazio. Ao esfriar o aço, depois de soldado na parte inferior, a tensão para manter o aço esticado é igual à tensão de escoamento do aço A36 ( 36 ksi = 250 MPa) pois 250/210.000 = 1,19 mm/m < 0,01 x 250 = 2,5 mm/m. Portanto, a força aplicada após o resfriamento será igual à força capaz de escoar a chapa de seção transversal 15 x 1,6 = 24 cm², isto é 0,0024 x250.000= 600 kN, valor superior à força necessária de 560 kN. É sempre conveniente neste tipo de reforço, adotar um valor ligeiramente acima do calculado pois, ao ser aplicada a força de 600 kN, haverá alguma acomodação e um pequeno encurtamento do concreto, o que acarretará uma diminuição da força efetivamente aplicada.

Um outro caso análogo se refere ao reforço de um pilar que recebe uma viga de transição. Um edifício importante em São Paulo foi projetado com um grande salão no térreo, com 15 m de vão e pé-direito de 8 m. Uma das vigas no teto do térreo, com 15 m, devia receber um pilar próximo ao meio do vão, que sustentava a caixa d'água superior e 18 pavimentos. Evidentemente, foi necessário utilizar a protensão para que a altura da viga não ficasse exageradamente grande. Foi utilizada a protensão parcial de tal modo que a viga pudesse resistir sem protensão a carga dos 8 primeiros pavimentos. Chegando ao 8° pavimento, já existia um carregamento considerável que estaria sendo resistido apenas pela armadura passiva. Só então é que se aplicariam 50% da protensão prevista, ficando o restante da protensão relegada a uma fase posterior da construção em que já estariam concretados mais 6 andares.

Os apoios da viga de transição foram previstos monolíticos com os pilares. A viga, com 100 x 150 cm ficava totalmente apoiada no pilar de fachada, porém apoiava somente numa área de 30 x 50 cm no pilar interno, cujas dimensões avantajadas de 30 x 300 cm serviam de limite à caixa de escadas. Dos 300 cm, 50 cm serviam de apoio à viga de transição. Os restantes 250 cm continuavam em todos os pavimentos superiores. Para evitar flexões indesejáveis no pilar, existia uma separação vertical entre a viga e o pilar, permitindo apoio para a viga apenas na sua saliencia de 50 cm, onde o pilar sofria uma descontinuidade.

O efeito da 1ª parcela da protensão, contrário ao efeito da carga vertical, produziria na viga uma contraflecha de aproximadamente 5 cm, equivalente ao valor de flecha devida à carga vertical até o 8° pavimento. A carga vertical produziria uma flecha positiva de 5 cm, ocasionando uma rotação da viga nas extremidades de mais ou menos 4 x 5/1500 = 0,013 rad = 0,8° .Sendo a altura da viga 150 cm, esta rotação faria abrir a fenda existente (cerca de 5 mm) entre a face vertical da viga e o pilar, de 0,013 x 150 = 2 cm. A ação superposta da flecha positiva de 5 cm e da contraflecha de 5 cm não originaria nenhuma rotação sensível nos apoios. O projetista da estrutura havia pensado corretamente, prevendo a aplicação de apenas 50% da protensão, somente depois que existisse um carregamento vertical apropriado. Inadvertidamente, decidiu-se aplicar a protensão quando apenas um pavimento acima da viga estivesse concretado. A contraflecha de 5 cm ocorreu sem a existência de uma flecha igual para contrabalançar. A fenda de 5 mm se fechou completamente e a viga, atuando como uma alavanca teria deslizado no apoio caso não existisse uma armadura de ligação viga-pilar.O resultado foi o que se indica esquematicamente na fig. 9: A parte saliente do pilar separou-se do restante, realizando a separação que a natureza exigiu.

Não é preciso dizer que o alarme foi impressionante, até que se verificasse que não existia perigo de desabamento. Com a continuação da obra, logo que se produzisse a flecha prevista, a situação iria melhorar. A fissura aberta, entretanto, nunca fecharia completamente. Tambem não era tranquilo esperar que a construção chegasse ao 8o pavimento. Nem era possível desmanchar a protensão aplicada, pois os trechos salientes de cordoalha já haviam sido cortados depois de terminada a protensão. A solução foi realizar um "estribo" horizontal na região fissurada, por meio de uma fita metálica protendida por meio de calor. A fig. 10 mostra o resultado do reforço.

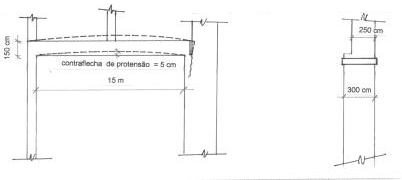
Fig. 9 - Trinca em pilar           Fig. 10- Tipo de reforço realizado.

Terceiro Exemplo: Viga protendida com cabo concordante

Este exemplo é uma adaptação de um caso real mais complexo (Ponte sobre o Rio Feio entre Guaraçaí e Junqueirópolis, SP), de uma viga de ponte, simétrica de dois tramos, sobre 3 apoios. Os vãos são de 21 m e o cabo resultante foi concebido de tal modo que, sob ação da protensão atuando sozinha, o ponto central de apoio não sofreria nenhum deslocamento para cima ou para baixo. Desta maneira não haveria hiperestáticos de protensão.

O cabo nestas condições é chamado em português "cabo concordante", expressão mais feliz correspondente à denominação alemã de "protensão a forma fiel". O cálculo dos efeitos da protensão pode ser feito como se a viga não tivesse apoios. Estes receberiam as mesmas reações verticais que vigas não protendidas. Não haveria transferência de reações do apoio central para os laterais.

A Fig. 11 representa o esquema da viga prevista para um Trem-Tipo de 450 kN e carga distribuida de 5 kN/m². No tabuleiro existem 4 vigas iguais separadas de 2,5 m.

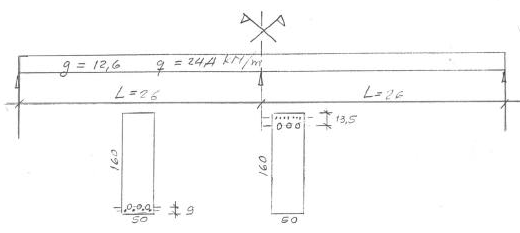
Fig. 11 - Esquema da viga de ponte, protendida com cabo concordante

O peso próprio do tabuleiro aplicado a cada viga de 50 x 160 cm é de 12,6 kN/m e a carga móvel, transformada em carga uniformemente distribuida é de 24,4 kN/m. Com estes dados, os momentos fletores no vão AB e no apoio B são respectivamente (a 1ª parcela é para carga permanente e a 2ª para carga variável já incluido o impacto):

M_AB = 817 + 1155 kN.m

|M_B | =1065 + 2061 kN.m

Usando a tabela para dimensionamento no ELU do "Manual de Concreto Protendido" (publicação da CSBM, por A .C.Vasconcelos, p. 30) tem-se:

No apoio: M_d = 1,3 x 1065 + 1,4 x 2061 = 2,079 MN.m

No vão: M_d = 1,3 x 817 + 1,4 x 1155 = 3,126 MN.m

Adotando f_ck = 34 MPa e protensão inicial com ?_pi = 6 ‰ = 6 mm/m tem-se com cobrimento d' = 13,5 cm

Braço de alavanca z = 0,888 x 1,465 = 1,30 m

Deformação do aço na ruptura da peça: ?_pd = 9,5 + 6 = 15,5 ‰

Tensão correspondente no aço: ?_pd = 1510 MPa

Área de aço necessária:

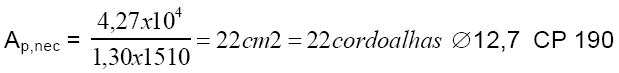
Serão adotados 3 cabos de 4 ? 12,7 (A_p = 12 cm²)

O complemento necessário será feito com armadura passiva de aço CA-50 trabalhando no escoamento na ruptura da peça ( pois 9,5 > 2,07 ‰):

A_s,nec = (22 - 12) x 1510/435 = 34,7 cm² = 7 ? 25

Foi adotada portanto a protensão parcial na fração de 55% de protensão (12/22 = 55%).

Procedento de modo análogo para o vão, os 3 cabos prolongados do apoio para as extremidades são suficientes com cobrimento de 9 cm.

O traçado correspondente do cabo é o da Fig.12.

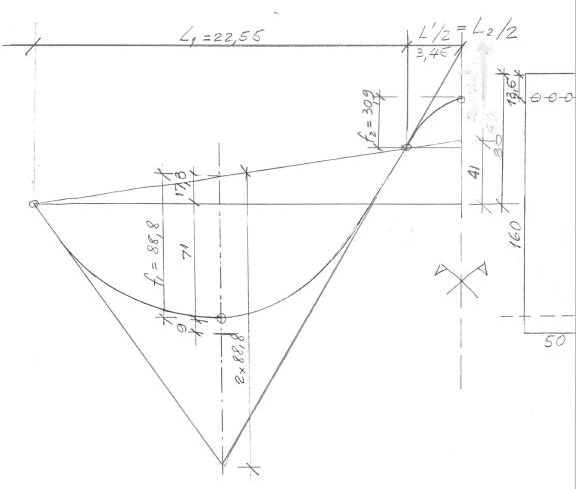
Fig. 12 - Desenho do cabo resultante composto de duas parábolas positivas com vão de 22,55 m e uma parábola negativa com vão de 2 x 3,45 = 6,9 m. Na realidade não se costuma adotar os cobrimentos positivos e negativos diferentes. Isto foi feito para se conseguir a condição de cabo concordante.

O traçado do cabo foi feito por tentativas, até que resultasse flecha numa no centro da viga de 52 m de vão com ação exclusiva da protensão. As pressões de desvio do cabo são, com os dados da Fig. 12:

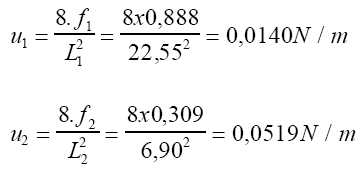
A flecha no meio do vão, sem o apoio central, causada pelas duas cargas distribuidas u₁ = 0,0140 N/m para cima em todo o vão e a carga u₁ + u₂ = 0,0140 + 0,0519 = 0,0659 N/m no trecho central de L' = 6,90 m vale:

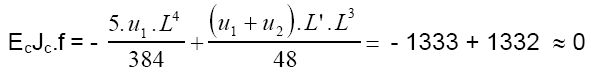
Para que isto aconteça é necessário que o cabo tenha cobrimentos diferentes nos vãos e no apoio central, o que não se costuma fazer. O normal é considerar o efeito do hiperestático de protensão e usar o mesmo cabo tanto para os vãos como para o apoio, complementando a deficiencia com armadura passiva.

Para melhor ilustrar o que acontece preparei um modelo feito de borracha, com furos acompanhando a trajetória do cabo resultante. Pela aplicação da protensão por meio de porca e rosca, percebe-se com clareza a deformação da peça, que, numa viga de concreto não se nota a olho nú. Deliberadamente não foram coladas as fatias de borracha, pois se notou que as borrachas não coladas apresentavam flechas muito maiores, e além disso, as regiões tracionadas facavam aparentes pela abertura das juntas. Nos trechos colados, a rigidez foi muito maior. Percebe-se tambem a influência do atrito, pois a ação da protensão foi aplicada numa só extremidade.

Fig.13 - Aspecto do modelo de aduelas de borracha com cabo concordante interno, conforme desenhado.

Quatro Exemplo: Cabos de protensão comprimidos

Os cabos usuais de protensão são tracionados e ancorados nas extremidades onde transmitem para o concreto por intermédio de suas ancoragens, por reação, a força neles aplicadas pelos macacos. O traçado do cabo é tal que ele atravessa em cada seção transversal da peça, a zona onde existem tensões de tração causadas pela carga de uso. Numa viga simplesmente apoiada, a zona de tração se situa na parte inferior, sendo a tração mais intensa nas vizinhanças do meio do vão, onde o momento é maior. O cabo geralmente acompanha o diagrama de momentos, sendo suas excentricidades maiores onde os momentos são maiores. Para cargas externas uniformemente distribuidas, o melhor traçado do cabo é parabólico.

Com excentricidades apropriadas, é possível equilibrar totalmente os momentos das cargas permanentes, cancelando toda tração existente. Entretanto, as forças aplicadas pelo cabo tracionado ao concreto, compreendem as forças de contato do cabo com o concreto e tambem as forças nas ancoragens. Quando estas ancoragens são centradas nos extremos da peça, essas forças possuem componentes axiais que comprimem uniformemente todas as seçòes, tanto na parte inferior como na superior. Essas compressões são úteis na parte inferior onde cancelam as trações existentes, porém na parte superior, onde a peça já está comprimida, agravam as compressões existentes.

Billig, no fim de 1950, solicitou patente na Inglaterra de um processo de protensão, no qual um tubo de aço com um cabo no seu interior (Fig. 14 [2]), era colocado dentro de uma fôrma da peça a ser moldada, num estado de elevada compressão.

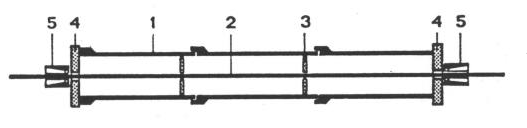
Fig. 14 - Cabo de compressão comprimido segundo Billig [2].

Legenda: 1 = tubo colocado em compressão dentro da peça de concreto na ocasião da moldagem, ficando perdido.

2 = cabo provisório, recuperável, servindo para comprimir 1

3 = septos para impedir a flambagem de 1

4 = placas de ancoragem de 2

5 = cunhas provisórias de ancoragem de 2

O sistema proposto por Billig nunca chegou a ser usado em obras. Entretanto, Reiffenstuhl em 1956 executou uma ponte municipal Classe I na Austria sobre o Rio Alm na circunscrição de Almegger. Essa ponte possui 76 m de vão em viga simplesmente apoiada com seção caixão de 2,50 m de altura e largura total de 10,50 m (Fig. 16 - [2]).

O sistema proposto por Reiffenstuhl está esquematisado na Fig. 15, com indicação de dois cabos parabólicos simétricos em relação ao eixo da peça. Os dois cabos são protendidos simultaneamente pela extremidade direita. Suas extremidades esquerdas são providas de ancoragens mortas. Ao ser aplicado o macaco para esticar o cabo inferior, seru apoio se dá exclusivamente no cabo comprimido superior. Desse modo não existe no concreto nenhuma resultante axial. As componentes normais ao eixo da peça são equilibradas internamente pelo concreto, não existindo qualquer reação externa. Toda reação de apoio provem apenas das cargas externas.

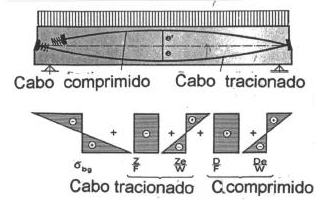
Fig. 15 - Esquema do processo imaginado por Reiffenstuhl, com um cabo tracionado e um cabo comprimido [2].

Reiffenstuhl não fornece detalhes em sua publicação, mas afirma que todos os problemas que sempre aparecem na execução foram resolvidos depois de diversos ensaios bem sucedidos.

Fig. 16 - Seção transversal no meio do vão da Ponte sobre o Rio Alm, executada com concreto B450 (45 MPa em cubos) na Austria [2].

A ponte sobre o Rio Alm foi protendida com 40 cabos tracionados e 48 cabos comprimidos (Fig. 16). Ao serem protendidos os cabos tracionados, os macacos eram apoiados contra os cabos comprimidos, havendo então uma compensação mediante ajuste adequado dos suportes.

A Fig. 17 mostra uma vista da ponte executada em 1956. De lá para cá não se falou mais neste tipo inusitado de protensão dando a impressão de que os custos não eram compensadores, não obstante tratar-se de uma proposta tecnicamente muito interessante. Como a resistencia do concreto melhorou muito a partir dos anos 70, é possível que os custos tenham ficado mais atraentes com o uso dos CAD (Concretos de Alto Desempenho) do que com os cabos comprimidos.

Fig. 17 - Ponte sobre o Rio Alm na Austria, projetada com cabos tracionados e comprimidos [2].

Quinto Exemplo: Os Troncos são realmente protendidos?

A própria natureza executa obras com os chamados "cabos comprimidos" do exemplo anterior. Quando se teve a idéia de aplicar tais cabos, como foi descrito no exemplo anterior, porovavelmente não se pensou em copiar a natureza. Deve ter sido uma casualidade em que se procurou tirar proveito do que parece racional, como a natureza vem fazendo há milhões de anos. Por causa da analogia existente é que se procurou introduzir aqui, como QUINTO EXEMPLO, o que já existe na natureza para ser copiado.

Pode-se afirmar que, de um modo geral a resistência à tração das madeiras usuais é da ordem de 4 vezes a respectiva resistência à compressão. É o contrário do que acontece com os materiais de construção, tais como concreto e ferro fundido, geralmente aplicados nas obras de engenharia: eles resistem melhor à compressão. Assim, por exemplo, o concreto resiste cerca de 10 vezes mais na compressão, o ferro fundido cerca de 8 vezes, o alumínio, 7 vezes. Gordon fornece em [3] uma tabela com alguns valores de referencia: madeira na tração com resistência de 100 MPa e na compressão apenas 27.

Tensões de Crescimento

Como crescem os troncos das árvores produtoras de madeira ? Para poder explicar isto de maneira rápida e inteligível, é aqui reproduzida uma figura esclarecedora extraida da obra de Burger & Richter [4], Fig. 18.

Fig. 18 - Esquema simplificado do modo de crescimento de um tronco [4]

A Fig. 18 esclarece como se processa o crescimento de maneira melhor do que palavras. Cada camada de crescimento, tanto do tronco como dos ramos, é adicionada à camada anterior como a superposição de uma série de casquinhas cônicas de sorvete. Cada camada se forma numa fina lâmina de células do tronco chamada cambio. A nova camada que se forma possui células que se ajustam às células da camada anterior como se estivessem empurrando-as para baixo, comprimindo-as. Por reação elas mesmas ficam tracionadas. O crescimento não se processa de maneira tão simples, porém não existe um modo rápido melhor de explicar o fenômeno. As células que crescem são internamente tracionadas e durante seu crescimento comprimem as células vizinhas. Dessa maneira, a tração que já existia na camada anterior vai diminuindo a cada nova camada acrescentada. As camadas mais internas deixam de possuir tração e passam a ser solicitadas somente à compressão. Pode-se afirmar que a tração é máxima na periferia e vai se transformando gradativamente em compressão, que atinge o máximo valor no centro. O diagrama de tensões ao longo de um diâmetro do tronco assume o aspecto da Fig. 19. Para um tronco cilíndrico, o diagrama numa seção transversal terá o aspecto de um volume gerado pela rotação daquele diagrama em torno do eixo do tronco.

A existência de tensões de tração num anel periférico do tronco é bastante favorável para aumentar a capacidade resistente aos esforços devidos ao vento. De fato, o vento atuando da esquerda para a direita, Fig. 20, produz tensões de tração na região esquerda do tronco ( a barlavento ) e tensões de compressão na região direita ( a sotavento). Superpondo estas tensões com as tensões próprias, originárias do crescimento, resultam tensões reduzidas de compressão a sotavento, melhorando a capacidade resistente do tronco. Ele se torna apto a resistir a ventos mais fortes. Em contrapartida, a barlavento as tensões de tração se somam, o que não constitui uma desvantagem, pois a resistência à tração da madeira é bem maior.

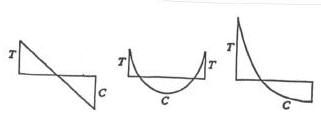
Fig. 19 - Diagrama de tensões internas equilibradas numa seção do tronco.

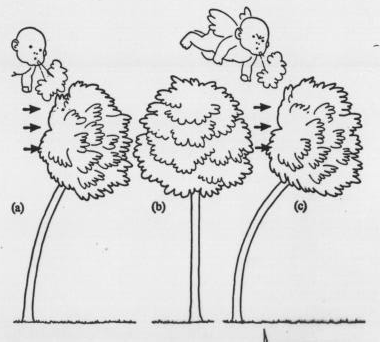
Fig. 20 - Diagrama explicativo da maior resistência do tronco em consequência da "protensão" [1].

As tensões próprias do crescimento podem ser consideradas como uma verdadeira protensão do tronco, porém às avessas do que acontece no concreto protendido. Neste, sendo a resistência do concreto à tração muito pequena, são as tensões de tração que devem ser evitadas ou diminuidas. Os cabos de protensão provocam o aparecimento de grandes tensões iniciais de pré-compressão no concreto, tornando-o assim apto a resistir trações elevadas. Nas árvores a "protensão" provoca o aparecimento de grandes tensões iniciais de pré-tração, tornando a madeira mais apta a resistir compressões elevadas.

Gordon cita em [3] que a "pré-tração" na parte externa do tronco chega a 14 MPa, valor bastante elevado se se considerar que a resistência à compressão da madeira pode ser apenas 27 MPa. Desta maneira, a capacidade do tronco de resistir a compressões aumenta cerca de 60% pois 27 x 1,6 - 14 = 26,5! Não foi possível descobrir qual a origem deste valor da protensão, que não é citado em nenhuma outra obra consultada.

Fato muito interessante citado por Gordon [3], refere-se ao uso de troncos inteiros para fabricação de mastros dos galeões e caravelas do passado. Engenheiros da época teriam preferido usar tabuas coladas de madeira, previamente escolhidas dentre as melhores, gruda-las com colas adequadas, usando cavilhas para garantir o funcionamento conjunto. No final teriam executado mastros "perfeitos" e controlados, com anéis de aço de quando em quando para dar uma segurança adicional e facilitar a fixação das velas. Não obstante todos estes cuidados e a perfeição da manufatura de tais mastros, os marinheiros "práticos" continuavam preferindo o uso de mastros feitos com troncos naturais dos quais era retirada apenas a casca externa, mantendo inalteradas todas as ondulações e mossas da madeira natural. Eles não sabiam explicar o porquê desta preferência mas insistiam que tais mastros eram mais resistentes! Hoje nós sabemos a justificativa daquela intuição: a protensão da madeira por meios naturais. Os mastros fabricados com madeira serrada ficavam sem a ajuda daquela protensão que desaparecia com o corte em tabuas.

Sexto Exemplo: A Arquitetura da Vida (segundo Ingber)

Com este título foi publicado um artigo revolucionário de Donald E. Ingber na revista Scientific American de Janeiro de 1998 [5]. Ingber é médico pesquisador do Departamento de Patologia e Cirurgia em Boston. Na última década, Ingber publicou vários trabalhos sobre a estrutura da célula reunindo conhecimentos de física, arquitetura e forma com os de biologia ([6] a [8]).

Do mesmo modo que Frei Otto em Stuttgart [9], que julga ser tudo na natureza nada mais do que PNEU - no sentido de membrana inflável - também Ingber referencia tudo como TENSEGRITY, isto é, estrutura formada por bielas comprimidas ligadas por fios tracionados . Ingber declara explicitamente que isto é extensamente válido desde o campo molecular onde proteínas e diversas outras moléculas se estabilizam por meio dos princípios que governam a "tensegrity", até os esqueletos dos vertebrados ou os orgãos dos organismos vivos.

TENSEGRITY não tem tradução em lingua portuguesa, mas poderia ser chamada “tensegridade”. É um têrmo em inglês, inventado por R. Buckminster Fuller na década de 50. É uma união de "tensional" - que significa em inglês "relativo à tração"- com "integrity", isto é "integridade". Tensegrity significa portanto algo que possui integridade, coesão, graças aos elementos (fios) tracionados. Para garantir a tração nos fios ( o que exige a aplicação prévia de alguma protensão!) devem existir elementos comprimidos que recebem as forças de tração e as equilibram por meio de compressões capazes de manter os pontos de junção imobilizados.

Fuller começou estudando os "domos geodésicos" (Fig. 21) que nada mais são do que cúpulas nas quais a superfície foi dividida em triângulos, cada elemento triangular sendo substituido por três barras capazes de resistir tanto à tração como à compressão, ligadas entre si.

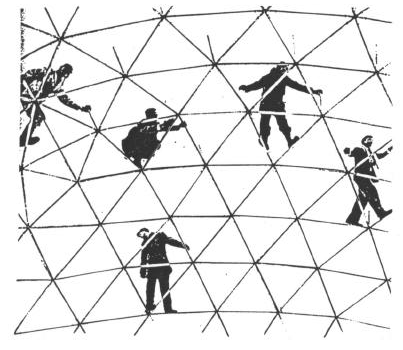
Fig. 21 - Domo geodésico de Buckminster Fuller [10]. Observando bem esta foto é possível notar a existência de hexágonos e também pentágonos!

Ao invés de uma cúpula com superfície contínua, Fuller obteve uma estrutura reticulada formada de barras articuladas em nós resistentes. Desde que as barras assim obtidas tivessem capacidade suficiente para resistir às forças de tração e de compressão sem sofrer flambagem, a estrutura seria estável. O preenchimento dos vazios por meio de um tecido de lona ou folhas finas de plástico ou alumínio, com função exclusiva de vedação, confere à construção condições favoráveis de uso como abrigo.

Este tipo de "tensegridade" cai numa categoria de estruturas resistentes pela forma, em que cada elemento pode resistir tanto à tração como à compressão, sendo o estado de tensão dependente das cargas que são aplicadas exclusivamente nos nós.

Outro tipo de "tensegridade" constitui uma segunda categoria de estruturas resistentes em que os elementos que resistem à tração (fios) são separados dos elementos que resistem à compressão (bielas) . Os elementos tracionados são contínuos, isto é, eles se encontram nos nós e continuam em direção a outros nós. Os elementos comprimidos são descontínuos, isto é, eles não se tocam entre si. Servem apenas de suporte aos elementos tracionados. Como a existência de tração ou compressão depende do valor e da posição das cargas, que são aplicadas apenas nos nós, é possível que, sob certos carregamentos, os elementos tracionados passem a receber compressões. Como esses elementos são apenas fios, na situação em que eles passem a receber compressões, flambam e se tornam inativos. É possível que a estrutura com os fios tornados inúteis, continue resistindo às mesmas cargas, mobilizando diferentemente os elementos resistentes rmanescentes. Se isto não for possível, a estrutura desaba. A fig. 22 mostra uma estrutura nestas condições, concebida como a mais simples que se possa imaginar.

Fig. 22 - Estrutura do tipo "tensegridade" com barras tracionadas contínuas e barras comprimidas descontínuas, imaginada por Fuller [10].

Existe entretanto a possibilidade de manter a estabilidade da estrutura inicial. Para isto basta aplicar aos fios uma tração prévia, maior do que a eventual compressão que venha a receber. Isto significa que os fios devem ser previamente esticados, antes de serem solidarizados na estrutura. Essa protensão permitirá que a estrutura tenha condições de resistir a qualquer sistema de cargas, desde que as compressões que estas cargas possam aplicar às barras, sejam satisfatoriamente resistidas: nas barras resistentes à compressão, separadas das demais barras análogas, desde que elas possuam rigidez suficiente para não sofrerem flambagem; nas barras não resistentes à compressão, isto é, nos fios, desde que elas possuam uma pré-tração superior à compressão que venha a existir. Tais estruturas podem ser deformadas por cargas externas até se transformarem num conjunto plano e no entanto voltarem a assumir a mesma configuração inicial quando as cargas forem retiradas. A protensão fica armazenada na estrutura sob a forma de energia potencial elástica. Qualquer carregamento externo modifica a energia armazenada, modificação que é devolvida uma vez cessado o carregamento.

Este tipo de "tensegridade" foi realizado pela primeira vez por Keneth Snelson, aluno de escultura de Buckminster Fuller nos anos 60.

Não sendo engenheiros, tanto Fuller como Snelson possuiam a mente livre e não contaminada pela matemática, para poderem raciocinar de maneira livre de conhecimentos preconceituosos. Dessa maneira, sem se ater às estruturas tradicionais, provavelmente Snelson começou a montar suas criações utilizando "canudinhos de refresco" como elementos resistentes à compressão, e "fios de linha" como elementos resistentes à tração. Supõe-se que deve ter feito diversos modelos para realizar criativamente novas formas pelo método de "tentativa e erro". Ao constatar que aplicando pequenas cargas, alguns fios ficavam frouxos, resolveu substitui-los por fitas elásticas previamente esticadas. Notou então que, até certo valor da carga aplicada, tais fitas elásticas não chegavam a se afrouxar totalmente. Dai em diante seu grau de criatividade permitiu ampliar a gama de modelos representativos de estruturas formadas por uma série CONTÍNUA de fios e uma série DESCONTÍNUA de bielas.

Ingber, mesmo não sendo engenheiro, teve a intuição de que as macroestruturas criadas por Fuller e por Snelson, poderiam se repetir no campo molecular. Os átomos são mantidos em suas posições por forças de atração ou repulsão de natureza elétrica. Essas forças, de valores enormes, são responsáveis pela integridade da matéria. Para realizar a fissão do átomo é necessário vencer tais forças daí resultando grande libertação de energia, fato evidenciado pelos efeitos da bomba atômica. Os átomos se reunem formando moléculas. As forças de atração entre átomos varia de acôrdo com a maneira de aproximação e o tipo de átomo envolvido. Essas forças de atração são caracterizadas pelo que chamamos "valências". Existem então as ligações simples ou duplas. Para realizar a separação, transformando uma molécula em outra, é necessária a colaboração de catalizadores (enzimas) que facilitam a anexação de um átomo por outro. A luz pode facilitar esssa transformação como acontece na fotossíntese. A ação do calor, de campos elétricos ou magnéticos, o bombardeamento por meio de partículas elementares dotadas de alta velocidade, são outros meios de interferir na composição da matéria. O fato é que a composição das moléculas deve obedecer a um tipo estrutural em que as bielas são as forças de atração entre átomos e os fios são representados pelas forças de repulsão. O equilíbrio de cada átomo (nó) é representado pela soma de todas as forças atuantes no nó, quer de atração (compressão) quer de repulsão (tração) exercida pelos nós vizinhos. Essas forças constituem a abstração de uma estrutura que possui uma integridade estrutural ( tensegridade ). Quanto mais estável for uma molécula, tanto mais eficientes são aquelas ligações estruturais. A estabilização de uma proteína, por exemplo, obedece ao princípio da já definida "tensegridade".

Ainda se conhece muito pouco da verdadeira estrutura molecular, sendo que apenas se descobriu algo através dos estudos da difração de raios X ou bombardeamento por neutrons.

Ingber julgou que, sendo a "tensegrity" válida tanto nas macro-estruturas dos engenheiros, como no campo molecular justificando a estabilização de proteínas, deveria ser aplicável tambem às células. Como interagem os elementos constitutivos das células ?

Frei Otto é partidário de que a célula é um PNEU, isto é, é uma membrana inflável [9] dentro da qual existe um líquido comprimido recebendo as forças que a membrana esticada exerce sobre ele. Otto explica assim o equilíbrio existente em que o elemento estrutural é somente uma membrana, isto é, um material que resiste exclusivamente à tração, qualquer que seja a direção, com igual capacidade resistente.

Ingber se volta para a estrutura que existe no interior da célula. Não é apenas um líquido comprimido, e todos os biólogos concordam que todas as células que possuem núcleo, possuem tambem no seu interior uma rede espacial de três elementos fundamentais [5]: a) micro-filamentos contendo actina; b) micro-túbulos contendo tubulina; c) filamentos intermediários contendo os polímeros vimentina, desmina, keratina. Todos estes elementos são proteínas ainda em processo de estudos.

Fig. 23 - Modelo de célula imaginada por Ingber e reproduzido pelo autor

Como no estudo das contrações musculares já é conhecida a atuação das proteínas actina e miosina, a maioria dos biólogos [5] concorda que uma rede tridimensional de filamentos no interior da célula forma um "esqueleto" denominado "citoesqueleto". Este conjunto forma uma estrutura sólida que pode mudar de forma e tambem pode se mover. O estudo da "tensegrity"aplica-se portanto igualmente ao campo celular.

Ingber montou o modelo da Fig. 24 para explicar como se deforma uma célula. O autor reproduziu este modelo com varetas de madeira e fios elásticos contínuos e o resultado foi realmente surpreendente, análogo ao que já havia obtido com o modelo da Fig. 23.

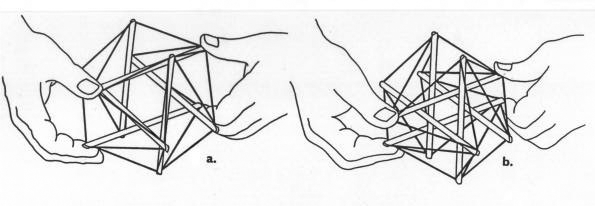
Fig.24 - Modelo de uma célula segundo Ingber, feito com varetas de madeira e fios elásticos [8].

Uma verdadeira revolução está acontecendo na interpretação dos estímulos mecânicos traduzidos em reações químicas que governam o crescimento. Há muito tempo sabe-se que os músculos se desenvolvem com o exercício. Mas é somente o estímulo freqüênte que produz efeitos significativos. Um atleta que pratica de vez em quando não observa efeitos importantes. Entretanto, quando o exercício é freqüênte os resultados são notáveis. A resposta à solicitação freqüênte não é novidade. Na engenharia tambem se sabe, de longa data, que não é a carga máxima que causa a fadiga e sim a solicitação freqüênte, ainda que de valor pequeno em relação à capacidade resistente. Uma árvore assolada por ventos freqüêntes cresce de maneira a poder resistir a tais solicitações. Não é contudo capaz de resisti-las se aplicadas "sem uma preparação adequada".

Até pouco tempo acreditava-se que a forma das células era controlada por diversos fatores: tensão superficial de sua membrana envolvente, pressões osmóticas, viscosidade do protoplasma (mais especificamente, do cito-esqueleto!), polimerização molecular [5]. Anos mais tarde Donald Ingber, revolucionou de maneira esplêndida todos os conceitos da época: estabeleceu um elo entre os estudos de engenharia, revolucionados por Buckminster Fuller (falecido em 1983) e as pesquisas biológicas. O elo estava nas estruturas imaginadas por Fuller, constituidas de barras tracionadas contínuas e barras comprimidas descontínuas. Ingber, num rasgo de genialidade, associou tais estruturas com as células. Estas seriam tambem constituidas por um grande número de filamentos e micro-tubulos comprimidos e independentes, ligados por elementos tracionados em continuação uns dos outros.

Os elementos tracionados de Fuller deviam ser "protendidos", isto é, previamente esticados. Dessa maneira a estrutura, ao receber algum carregamento externo que causasse compressão naqueles elementos, não os deixaria "bambos" mas apenas "menos tracionados". Isto é fundamental. Para qualquer tipo de carregamento, os elementos tracionados continuam tracionados. Era portanto indispensável que existissem elementos comprimidos capazes de equilibrar as tensões de tração instaladas. Este é o segredo das estruturas de Fuller, para manutenção de sua integridade. A isto Fuller atribuiu um nome: "tensegity" ou "integridade por meio de tração". O importante no caso é existir uma sequencia contínua de elementos tracionados com tensões prévias, equilibrada por elementos comprimidos convenientemente dispostos.

As células segundo Ingber, teriam uma estrutura semelhante. Sua membrana não é um elemento contínuo ( um PNEU segundo a expressão de Frei Otto [9]): é constituida por uma malha bastante fina com "tensegridade" estrutural. Nos espaços entre as barras poderia haver passagem de líquidos e isto seria interpretado como "osmose". No interior da célula existiria tambem uma estrutura denominada "cito-esqueleto" constituida da mesma maneira: elementos tracionados contínuos e elementos comprimidos descontínuos. O núcleo estaria como que "dependurado" naquele emaranhado com "tensegridade" estrutural, sendo ele próprio outra estrutura do mesmo gênero.

Graças à protensão existente nos elementos tracionados, qualquer estímulo externo de natureza mecânica, elétrica, térmica, acarreta uma resposta imediata que provoca variação das tensões de tração. A esta variação correspondem compressões nos elementos descontínuos ou nas regiões onde as células se apoiam. Estas regiões constituem a "matriz extra-celular" .É ali que se estabelece o equilíbrio com as solicitações externas.

Ingber imagina que este é o modo como os tecidos são construidos. Esclarece em escala maior do que a das células, que nossos ossos são os elementos indispensáveis para equilibrar as forças da gravidade. Eles são equilibrados mecanicamente por meio dos seus elementos tracionados (músculos e tendões). Esse mecanismo se repete nos insetos que, ao invés de ossos, possuem um exo-esqueleto, e nas plantas, através das pressões de turgescência dentro das células, que correspondem tambem a uma protensão, como mecanismo de equilíbrio.

Bibliografia:

[1] MÖLL, H. - Hormigón pretensado , Editora GG, Barcelona 1958

[2] REIFFENSTUHL, H. - Druckspannbewehrung, ein neues Konstruktions- element zur entscheidenden Steigerung der Tragfähigkeit von Stahlbeton- und Spannbetonquerschnitten, in DK 624.012.454/.464.046 (??)

[3] GORDON, J.E. - Structures (or why things don't fall down ), Da Capo Press (Penguin Books Ltd.), 1978 p. 280-3.

[4] BURGER, L.M. e RICHTER, H.G. - Anatomia da Madeira, Livraria Nobel S.A., São Paulo, 1991, p. 35

[5] INGBER, D.E. - The Architecture of Life, in Scientific American, Jan. 1998

[6] INGBER, D.E. - Cellular tensegrity: defining new rules of biological design that govern cytoskeleton, in Journal of Cell Science 104, UK 1993, p. 613-27.

[7] INGBER, D.E. -Tensegrity: The Architectural Basis of Cellular Mechanotransduction, in Annual Review of Physiology, vol. 59, 1997, p. 575-99

[8] INGBER, D.E. et al. - Cell Shape, Cytoskeletal Mechanics and Cell Cycle Control in Angiogenesis, in Journal of Biomechanics , vol. 28 No. 12, 1995, p. 1471-84.

[9] THYWISSEN,C. et al. - Growing and Dividing Pneus, publicação IL19 do Instituto de Estruturas Leves de Stuttgart, 1979.

[10] BALDWIN, J. - Bucky Works - Buckminster Fuller's Ideas for Today, Johm Wiley & Sons, 1996.

[11] VILNAY, O . - Tensegric Shells (in R. NARAYANAN, Shell Structures: Stability and Strength, Elsevier Applied Science 1985, Chapter 10).

[12] PUGH,A . - An introduction to tensegrity, University of California Press, Berkeley 1976.