NBR6118:2003 - Mais sobre o dimensionamento de pilares
No dia 30 de março deste ano, a tão comentada NBR6118:2003 “Projeto de estruturas de concreto armado - Procedimento" completará oficialmente um ano de vigência exclusiva, isto é, sem a presença paralela da antiga NB1-1978.
Diversas inovações foram incorporadas ao novo texto e estão sendo adaptadas de forma gradativa no nosso dia-a-dia. Inúmeras análises, discussões e comparações circularam nas comunidades da internet, em cursos, em congressos, etc. Um assunto porém, a meu ver, ainda tem gerado bastante dúvidas, e até em certos pontos, controvérsias. Trata-se do dimensionamento de pilares.
Este tema, não só pela sua indiscutível relevância no contexto de um projeto estrutural, vem também chamando a atenção de muitos engenheiros devido a um outro fator: significativas alterações no consumo de aço. No Encontro Nacional de Engenharia e Consultoria Estrutural (ENECE) realizado em São Paulo em 2004, inclusive, o prof. Francisco Graziano proferiuuma palestra exatamente sobre este assunto.

Resumidamente, as principais modificações que influenciaram diretamente no dimensionamento de pilares são:
- Adoção do M1d,mín para consideração das imperfeições geométricas locais.
- Novo comprimento de flambagem le.
- Novo índice de esbeltez limite λ1.
- Novas formulações para análise local em 2ª ordem.
- Introdução da análise dos efeitos localizados em pilares-parede.
Diversos estudos iniciais revelaram que em pilares comuns, isto é, aqueles que não são pilares-parede, a aplicação destas prescrições pode ocasionar uma certa diminuição no consumo de armaduras. Quantificar o valor desta redução, ou mesmo generalizá-la, é uma tarefa complicada. “Cada caso é um caso.”
Até então, já havia me deparado com as mais diversas situações: casos em que a armadura não reduzia, casos com queda de 10%, de 15%, ..., até que, nesta semana, constatei num determinado lance de pilar uma redução de 70% no consumo de aço.
Tal fato me deixou bastante surpreso. Vejamos os seus dados.
A. Dados do exemplo
O pilar em questão está localizado no mezanino de um edifício, possui seção tranvsersal com dimensões de 210cm X 30cm e pé-direito duplo em torno de sua direção menos rígida igual a 6,0 m.
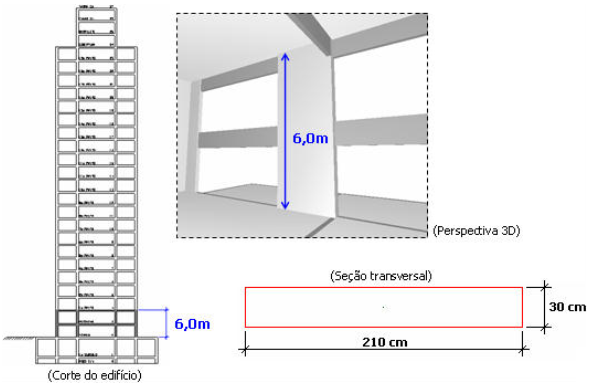
Apesar de possuir dimensões que o caracteriza como um pilar-parede (B > 5.H), o momento fletor em torno da direção de maior rigidez não gerava efeitos localizados em seus extremos. Diante disso, e também para simplificar os cálculos, vamos considerar a seguir somente as seguintes solicitações:
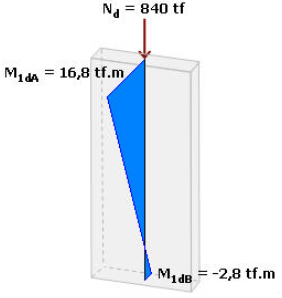
Demais dados necessários:
- Concreto C35; ɣc = 1,4
- Aço CA50; ɣs = 1,15; Es = 210.000MPa
- ɣf = 1,4; ɣf3 = 1,1
- c = 2,5 cm
B. Dimensionamento segundo as prescrições da NB1-1978
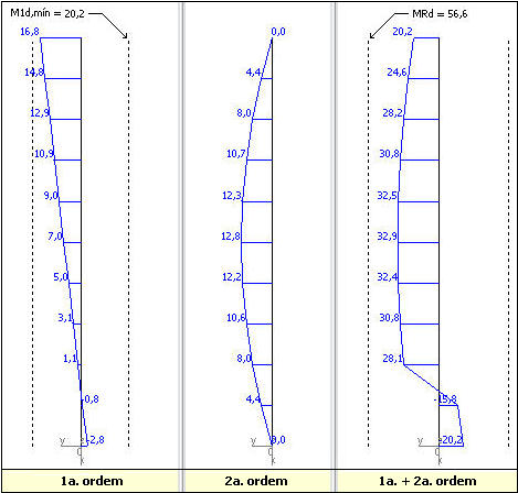
- Índice de esbeltez do pilar = 3,46*6 / 0,3 = λ = 69,3 > 40 (tem que considerar 2ª ordem)
- Excentricidade inicial no meio do lance = 0,6*(1680/840) + 0,4*(-280/840) = ei = 1,07 cm
- Excentricidade acidental aditiva = ea = 2,00 cm
- Força normal adimensional = 840 / [(2,1*0,3)*(3500/1,4)] = Ni = 0,53
- Curvatura aproximada = [0,0035+(500/1,15)/210000] / [(0,53+0,5)*0,3] = 1/r = 0,018 m-1
- Excentricidade de 2ª ordem = (36/10) * 0,018 = 0,0647 m = e2 = 6,47 cm
- Excentricidade total = 1,07+2,00+6,47 = etot = 9,54 cm
- Momento total de cálculo = 840*0,0854 = Md,tot = 80,1 tf.m
- Armadura necessária = As,nec = 104 cm2 (1,7%)
C. Dimensionamento segundo as prescrições da NBR6118:2003
- Excentricidade mínima de 1ª ordem = 0,015+0,03*0,3 = 0,024 m = e1,mín = 2,40 cm
- Momento mínimo de 1ª ordem = 840*0,024 = M1d,mín = 20,2 tf.m
- M1dA < M1d,mín αb = 1,0
- Índice de esbeltez limite = {25+12,5*[(1680/840)/30]} = 25,8 < 35 λ1 = 35
- Índice de esbeltez do pilar = λ = 69,3 > 35 (tem que considerar 2ª ordem)
- Excentricidade inicial no meio do lance = 1,0*1680/840 = ei = 2,00 cm < e1,min
- Força normal adimensional = 840 / [(2,1*0,3)*(3500/1,4)] = Ni = 0,53
- Armadura mínima = 0,15*840/(50000/1,15) = 29 cm2 > 0,004*AcAs,mín = 29 cm2
C.1 Pelo método do pilar-padrão com curvatura aproximada
- Curvatura aproximada = 0,005 / [(0,53+0,5)*0,3] = 1/r = 0,016 m-1
- Excentricidade de 2ª ordem = (36/10)*0,016 = 0,0581 m = e2 = 5,81 cm
- Excentricidade total = 2,40+5,81 = etot = 8,21 cm
- Momento total de cálculo = 840*0,0821 = Md,tot = 68,9 tf.m
- Armadura necessária = As,nec = 73 cm2 (1,2%)
C.2 Pelo método do pilar-padrão com rigidez kappa aproximada
- Rigidez adimensional aproximada = kappa = 34,8
- Excentricidade de 2ª ordem = 3,82 cm
- Excentricidade total = 2,40+3,82 = etot = 6,22 cm
- Momento total de cálculo = 840*0,0622 = Md,tot = 52,3 tf.m
- Armadura necessária = 27cm2 < As,mín = As,nec = 29 cm2 (0,5%)
C.3 Pelo método do pilar-padrão acoplado a diagrama N,M,1/r
- Adotando uma armadura longitudinal que atenda a As,mín = 16 ? 16 = 32 cm2
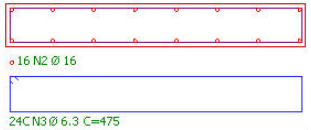
- Diagrama N,M,1/r
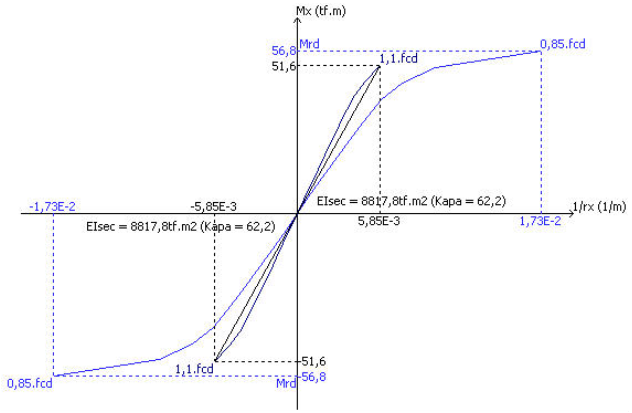
- Momento resistente último de cálculo = Mrd = 56,8 tf.m
- Rigidez adimensional aproximada = kappa = 62,2
- Excentricidade de 2ª ordem = 1,26 cm
- Excentricidade total = 2,40+1,26 = etot = 3,66 cm
- Momento total de cálculo = 840*0,0366 = Md,tot = 30,7 tf.m
- O pilar passa com a configuração de armadura adotada (32,2 cm2).
C.4 Pelo método geral
- Adotando a mesma armadura longitudinal anterior = 16 ɸ 16 = 32 cm2
- Excentricidade de 2ª ordem = 1,52 cm
- Excentricidade total = 2,40+1,52 = etot = 3,92 cm
- Momento total de cálculo = 840*0,039 = Md,tot = 33,0 tf.m
- O pilar passa com a configuração de armadura adotada (32,2cm2).
D. Resumo dos resultados
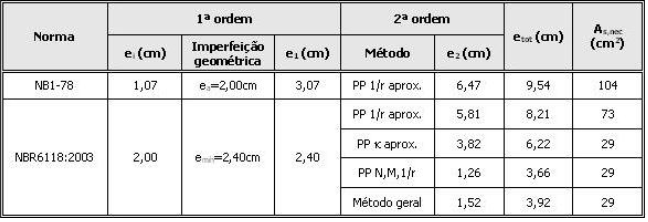
Notem a redução de 30% de armadura em relação a NB1-1978 quando da utilização do método do pilar-padrão com curvatura aproximada.
Notem a redução de 70% de armadura em relação a NB1-1978 quando da utilização dos métodos da rigidez aproximada, pilar-padrão acoplado a diagrama N,M,1/r e método geral.
Mais uma curiosidade: se fosse utilizado o processo Ω preconizado pela NB1-60, a armadura necessária também seria a mínima (29 cm2).
E. Comentários
Diante dos resultados do exemplo que acaba se ser analisado, arrisco-me então a fazer alguns comentários sobre o assunto. Notem o seguinte: a grande maioria deles está baseada em informações que outros colegas já haviam alertado, ou seja, somente estou reafirmando o que já havia sido colocado.
Sob ponto de vista matemático, isto é, da aplicação direta das fórmulas propostas pela NBR6118:2003, a redução no consumo de aço me parece justificada. O cálculo dos efeitos de 2ª ordem segundo os novos métodos mais precisos (rigidez kappa, diagrama N,M,1/r e método geral) indicou, até certo ponto, uma imprecisão do método mais aproximado (1/r aproximada). No entanto, sob ponto de vista de engenharia, acredito que a redução de armadura foi um tanto exagerada.
Muito embora a eficiência de um pilar não esteja atrelada integralmente a quantidade armadura, mas sim também pela quantidade e qualidade do concreto existente, o que mais me chama atenção no exemplo analisado é a consideração das imperfeições geométricas. A existência das mesmas não estão sob nosso controle durante o projeto. Na realidade, o que nós, engenheiros estruturais, estamos fazendo é tentar prever uma situação que certamente irá ocorrer durante a execução do pilar, seja em menor ou maior magnitude. É um problema complicado, e que precisa ser mais estudado. O pilar é um elemento extremamente sensível às imperfeições geométricas.
Sou favorável a adoção de coeficientes de segurança diferenciados por elemento (um para vigas, um para pilares, um para lajes, ...). Precisamos dar mais segurança para os elementos mais importantes da estrutura.
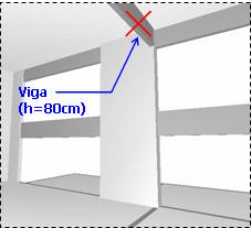
O item 15.6 da NBR6118:2003 que define o valor do comprimento le deve ser aplicado com extrema ressalva. No pilar analisado, por exemplo, se a viga (h = 80 cm) que chega no topo do lance fosse considerada como elemento de travamento (o que não é verdade), o valor adotado no cálculo seria: le = l0 + h = 5,2 + 0,3 = 5,5 m. Isto, de forma equivocada, reduziria ainda mais a armadura final.
A excentricidade de 2ª ordem calculada pelo método do pilar-padrão com curvatura aproximada segundo a formulação da NBR6118:2003 é 10% menor que a da NB1-1978, apesar do método ser o mesmo. Esta diferença é ocasionada pela alteração no cálculo da curvatura.
A aplicação do momento mínimo de 1ª ordem segundo a proposta que o eng. Graziano apresentou no ENECE2004 me parece bastante coerente.
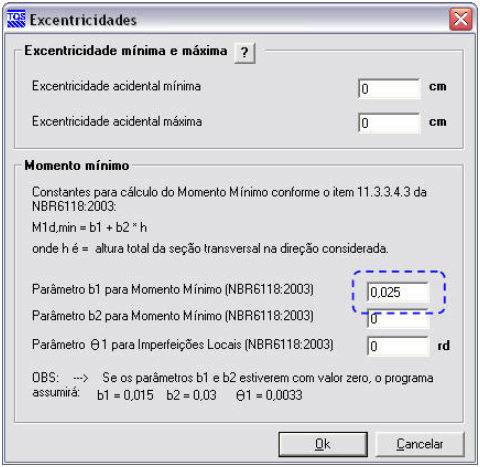
E. Dica para usuários TQS
A redução da armadura no exemplo anterior foi um tanto brusca, muito embora esteja exatamente de acordo com às prescrições da nova norma. O eng. Nelson Covas indicou, então, uma alternativa bastante interessante que torna o dimensionamento mais seguro.
Eis a dica: os coeficientes da fórmula do M1d,mín estão parametrizados no arquivo de critérios de projeto do TQS-Pilar (item botão ). Configure o coeficiente b1 = 0,025 de tal forma a acrescentar mais 1cm na excentricidade mínima.
Utilizando b1 = 0,025 no dimensionamento do pilar analisado, a armadura necessária (método do pilar-padrão com rigidez kappa aproximada) sobe para 60cm2.
Eng. Alio Kimura
TQS Informática Ltda.
