Efeitos do vento sobre edifícios de alvenaria estrutural

Mensagem originalmente postada no Grupo Alvenaria

Nos últimos vinte anos, a construção civil brasileira tem utilizado com sucesso o sistema construtivo de alvenaria estrutural. Pode-se considerar como construção pioneira, no ano de 1967, um edifício de apartamentos de quatro pavimentos em São Paulo, segundo Schumacher (2000). Dessa época até os dias atuais a alvenaria estrutural ganhou impulso no Brasil e hoje é possível encontrar esse tipo de construção em quase toda a extensão do País. Pelo seu pioneirismo, a região Sudeste, principalmente São Paulo, já utiliza esse sistema construtivo em empreendimentos de alto padrão. São construídos edifícios com mais de 15 pavimentos sobre transições de concreto armado. Obras desse porte só são possíveis, graças ao esforço conjunto das construtoras, das universidades e dos institutos de pesquisa para aprimorar a metodologia de construção, a qualidade dos materiais empregados, assim como os modelos de cálculo estrutural do edifício. No intuito de contribuir com o aperfeiçoamento do cálculo estrutural, avaliou-se um modelo matemático para análise dos efeitos do vento. Tal modelo leva em consideração o efeito tridimensional da estrutura e a participação dos lintéis no contraventamento.

Nos casos de edifícios mais altos, devido ao maior impacto dos efeitos do vento, o sistema de contraventamento tem papel fundamental no comportamento da estrutura. Dessa forma, torna-se importante a busca por modelos que representem melhor o comportamento do edifício sob as ações horizontais. Com esse modelo mais representativo é possível obter reduções dos esforços internos condizentes com o comportamento da estrutura. Assim, torna-se possível dimensionar paredes com blocos de menor resistência à compressão, reduzir a quantidade de armadura não-construtiva ou, até mesmo, considerar menos paredes estruturais para o edifício.

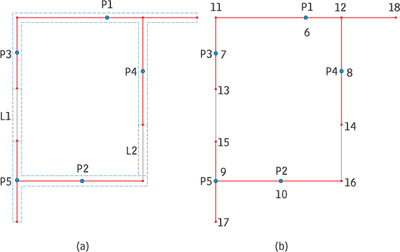
Figura 1 - Planta baixa da modelagem dos painéis de contraventamento: (a) Definição das paredes e inclusão de lintéis, (b) Incidência das barras na modelagem

Modelo teórico para análise

A modelagem descrita a seguir pode ser considerada, no âmbito dos modelos com elementos barra, como uma das mais completas. As paredes de contraventamento tornam-se mais discretas por elementos barra tridimensional, com seis graus de liberdade em cada extremidade - duas translações e duas rotações em relação a dois eixos transversais, e uma translação e uma rotação em relação a um eixo axial. Essas barras possuem as características geométricas das seções transversais retangulares das paredes, e são posicionadas nos correspondentes centros de gravidade.

Em projeto de edifícios de alvenaria estrutural é prática comum considerar o efeito de interação entre paredes que se interceptam. No modelo teórico em questão, barras horizontais rígidas simulam esses efeitos, assim como as excentricidades inerentes às forças de interação. Como essa interação é associada ao surgimento de forças cortantes verticais, é necessário articular a extremidade das barras rígidas que a simulam. Existe, também, a possibilidade de inclusão de lintéis no modelo, Figura 1 (a).

O comprimento e a quantidade de barras rígidas na modelagem dependem das interseções que ocorrem entre as paredes e da inclusão ou não dos lintéis. Observe-se a Figura 1 (b). Cada parede possui um nó no centro de gravidade da seção e aqueles definidos pela interseção entre paredes. O nó do CG é utilizado na incidência das barras verticais. Os nós de interseção, juntamente com o nó do CG, determinam a incidência das barras rígidas. De acordo com a Figura 1(b), a parede P1 possui três barras rígidas: a primeira do nó 11 ao 6, a segunda do nó 6 ao 12, e uma terceira do nó 12 ao 18. Na primeira barra rígida, a extremidade inicial é articulada, pois o nó 11 determina um ponto extremo na modelagem da parede, e a extremidade final permanece sem liberação de vínculos, pois o nó 6 determina um ponto interno na modelagem. A segunda barra rígida apresenta as duas extremidades contínuas, pois os nós 6 e 12 determinam pontos internos na modelagem. A terceira barra rígida possui extremidade inicial contínua e extremidade final articulada. Essa última barra pode ser excluída, caso não apresente interseção em sua extremidade final com um lintel ou outra parede.

Se os lintéis forem incluídos no modelo, suas extremidades devem possuir ligação contínua com as extremidades das barras horizontais rígidas. Quanto à laje, sua simulação é feita por um diafragma rígido em seu plano.

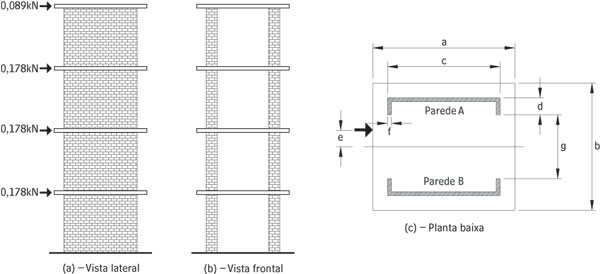
Figura 2 - Modelo reduzido ensaiado por U. C. KALITA and A. W. HENDRY (1970)

Validação do modelo teórico

Para validar o modelo teórico proposto foi utilizado o estudo experimental apresentado por KALITA U. C. and HENDRY A. W. (1970). O estudo consistiu na análise experimental de uma estrutura construída com tijolos maciços cerâmicos na escala 1:6 e composta de duas paredes simétricas e quatro lajes, Figura 2 (b).

Durante o ensaio foram aplicadas cargas verticais para simular a pré-compressão das paredes, e o modelo teórico de análise considerou a variação do módulo de deformação transversal G com a pré-compressão segundo os resultados apresentados em KALITA U. C. and HENDRY A. W. (1969). No modelo de barras, esse efeito foi considerado, ao se utilizar a relação entre os módulos E e G, obtendo-se os seguintes resultados: E=2.596 MPa para as paredes na base da estrutura, E=2.078 MPa entre a primeira e segunda lajes, E=1.602 MPa entre a segunda e terceira lajes e E=1.213 MPa entre a terceira e quarta lajes.

Com o emprego de macacos hidráulicos foram aplicadas forças horizontais de intensidades 0,178 kN, nas lajes intermediárias, e 0,089 kN na última laje, todas com excentricidade e=7,62 cm.

O modelo reduzido apresentava as seguintes dimensões: a = 50,80 cm; b = 50,80 cm; c = 44,14 cm; d = 7,62 cm; f = 1,75 cm; g = 28,90 cm; pé-direito medindo 43,18 cm; e laje com espessura de 2,54 cm.

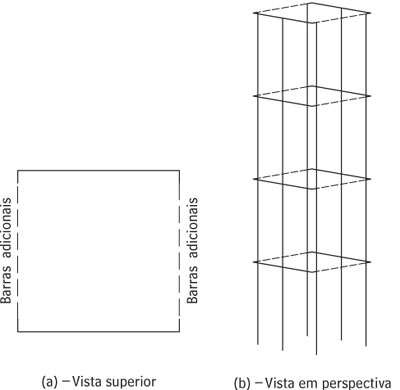
Figura 3 - Modelo de pórtico tridimensional para o ensaio

Para validação do modelo de pórtico tridimensional, foram comparados os deslocamentos horizontais das lajes. A modelagem teórica desenvolvida com o método dos elementos finitos foi extraída de KALITA U. C. and HENDRY A. W. (1970). No modelo de pórtico tridimensional, a contribuição da laje foi simulada considerando-se barras horizontais adicionais com módulo de deformação E=30.337 MPa e características geométricas correspondentes à espessura da laje e à largura colaborante segundo recomendações de KALITA U. C. and HENDRY A. W. (1969). Essas barras adicionais interligam as barras verticais dos trechos menores das paredes A e B.

Observando-se os gráficos dos deslocamentos da Parede A, Figura 4(a), percebe-se que os resultados do modelo de pórtico tridimensional praticamente coincidiram com o modelo em elementos finitos. No caso da parede B, Figura 4(b), o modelo de pórtico tridimensional obteve resultados muito próximos do experimental, evidenciando a qualidade da modelagem. Nessa análise, a variação dos deslocamentos entre as duas paredes, rotação da laje, foi maior no modelo de pórtico tridimensional. Isso pode ser atribuído ao tipo de modelagem utilizada para tornar a laje mais discreta. O modelo em elementos finitos permite que seja feita uma atenuação mais refinada, principalmente nas regiões de ligação da laje com a parede.

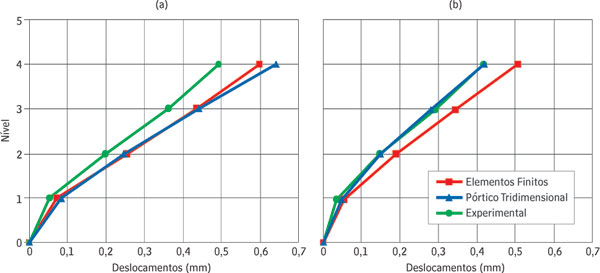
Figura 4 - Deslocamentos horizontais: (a) Parede A e (b) Parede B

Edifício exemplo

Como aplicação do modelo proposto foi analisado um edifício de sete pavimentos, representativo da prática de construção em alvenaria estrutural empregada no país. A Figura 5(a) ilustra a planta do pavimento tipo, que possui pé-direito medindo 2,80 m, enquanto a Figura 5(b) ilustra o diagrama unifilar das paredes consideradas no sistema de contraventamento. Foram avaliados quatro modelos distintos para a análise estrutural do edifício: o modelo 1 corresponde ao de paredes isoladas sem inclusão das deformações por cisalhamento das paredes; o modelo 2, ao de paredes isoladas considerando-se as deformações por cisalhamento; o modelo 3, ao pórtico tridimensional sem a inclusão dos lintéis; e o modelo 4, ao pórtico tridimensional com a participação dos lintéis. Em todos os modelos as deformações por cisalhamento das paredes são consideradas de modo aproximado. Dos resultados obtidos foi dado destaque aos deslocamentos horizontais ao nível dos pavimentos, à distribuição dos esforços cortantes entre os painéis e, quando conveniente, à distribuição de momentos fletores.

Foram considerados blocos com resistência variando de 6,0 MPa a 4,5 MPa da base ao topo, adotando-se módulo de deformação E = 2.960 MPa para todas as paredes. O carregamento devido ao vento foi determinado segundo a NBR 6123, considerando-se velocidade básica V0 = 38 m/s e edifício de classe 2 e categoria 4. Em todos os modelos foram consideradas forças horizontais segundo as direções principais X e Y, coincidentes com o centro geométrico de cada pavimento.

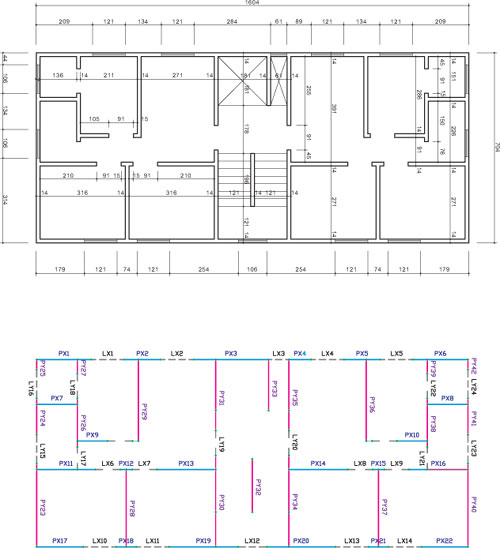
Figura 5 - Pavimento tipo do edifício analisado: (a) Arquitetura e (b) Diagrama unifilar dos painéis de contraventamento

O gráfico dos deslocamentos, Figura 6, mostra o ganho de rigidez dos modelos 3 e 4 em relação aos modelos 1 e 2. O modelo 3 apresentou reduções consideráveis, da ordem de 14%, no deslocamento do topo da estrutura, em relação ao modelo 1. O modelo 4 demonstrou o efeito benéfico da consideração dos lintéis, reduzindo ainda mais os deslocamentos. Esses lintéis aumentam substancialmente a rigidez do edifício devido à formação de painéis bastante longos. Isso permite que se manifeste uma interação mais intensa entre os elementos estruturais do sistema de contraventamento.

É importante alertar para o fato de que essas análises foram desenvolvidas considerando-se comportamento elástico linear da estrutura, não se avaliando, portanto, o grau de fissuração e a perda de rigidez dos lintéis.

Os dois modelos extremos, 1 e 4, foram comparados mediante a distribuição dos esforços cortantes, Figura 7(a). As diferenças máximas ocorreram na parede PX3 para a direção X, e PY30 e PY34 para a direção Y, com valores percentuais de 29% e 28% respectivamente. No caso das paredes PY30 e PY34, seus esforços se reduziram de 41,3 kN para 29,7 kN, valores obtidos com os modelos 1 e 4 respectivamente. Nos gráficos de distribuição de esforços cortantes, percebe-se claramente a tendência de redistribuição, ao se utilizar os modelos 3 e 4.

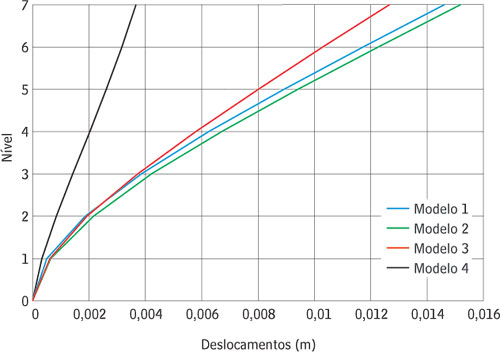
Figura 6 - Deslocamentos horizontais ao nível dos pavimentos

As análises com os modelos 3 e 4 objetivam avaliar o efeito dos lintéis no sistema de contraventamento. A consideração dos lintéis implica em redução nos deslocamentos, e também em reduções nos esforços cortantes e momentos fletores absorvidos pelas paredes, Figura 7(b) e Figura 8, respectivamente. O decréscimo no esforço cortante máximo (paredes PY30 e PY34) foi da ordem de 10%, enquanto no momento fletor máximo atingiu 53%. Com a consideração dos lintéis, surgem forças normais excêntricas nas paredes. Isto pode explicar a maior diferença associada ao momento fletor, pois essas forças originam reações verticais formando um binário resistente ao momento de tombamento da estrutura. Cabe ressaltar que o decréscimo elevado dos momentos implica em acréscimo das forças normais nas paredes.

Os lintéis mais solicitados, LY19 e LY20, apresentam esforço cortante V=18,5 kN, Figura 9. Foram considerados blocos com resistência característica fbk = 6,0 MPa no 1o e 2o pavimentos. Adotando eficiência h = 0,8, a tensão de cisalhamento admissível fcis1 = 0,20 MPa impõe o limite da solicitação de cisalhamento no lintel, para que seja dispensada a utilização de barras verticais/estribos.

Os referidos lintéis possuem seção transversal com b=14 cm e d=55 cm, de modo que resultam numa solicitação de cisalhamento t=0,24 MPa, indicativa da necessidade de reforço com estribos. A máxima tensão tangencial permitida para a alvenaria pode ser, nesse instante, tomada igual a fcis2=0,55 MPa. A armadura, calculada de acordo com a NBR 10837, deve possuir área As=0,31cm2 distribuída em cada furo dos blocos (espaçamento de 15 cm), correspondendo por exemplo, a f 6,3 por furo para estribo de um ramo.

Como o grauteamento do lintel seria inevitável devido à presença dos estribos, torna-se interessante analisar a alternativa de prismas cheios. Desse modo, dobra-se a resistência de prisma, resultando numa tensão admissível fcis1 =0,27 MPa. Nesse caso, seria suficiente o grauteamento de toda a seção do lintel, sem necessidade de estribos.

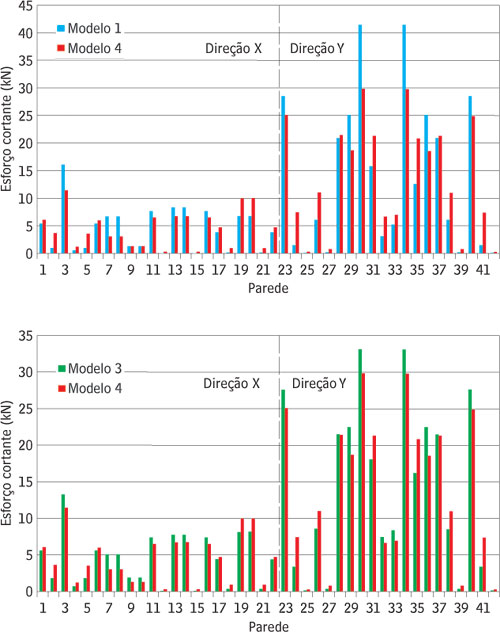
Figura 7 - Distribuição dos esforços cortantes entre os painéis de contraventamento com atuação do vento segundo as direções X e Y

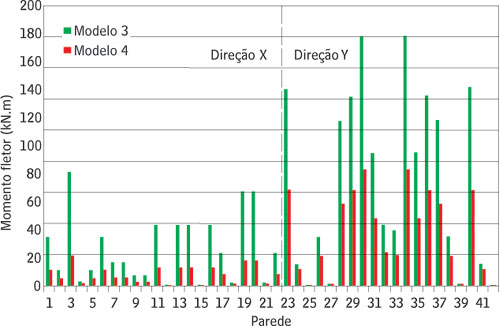
Figura 8 - Distribuição dos momentos fletores entre as paredes de contraventamento com atuação do vento segundo as direções X e Y

Comentários finais

O efeito do vento em edifícios de alvenaria estrutural pode ser analisado por vários modelos. Dentre esses modelos, um modelo tridimensional foi estudado e validado mediante comparação com resultados experimentais, obtendo-se boa aproximação. Além disso, utilizou-se um edifício exemplo para ser analisado com esse modelo tridimensional e com o de barras isoladas comumente empregado em projetos estruturais.

A análise do edifício exemplo destacou as alterações que podem ocorrer na distribuição dos esforços, ao se adotar um ou outro modelo de análise. Dos modelos avaliados, aquele que toma partido dos lintéis apresentou os menores valores de deslocamentos e esforços internos, notadamente os momentos fletores. Todas as análises feitas demonstram a representatividade do modelo tridimensional, apontando-o como uma alternativa viável para representação do comportamento estrutural de edifícios de alvenaria estrutural submetidos a ações horizontais. Como vantagens associadas a esse modelo de cálculo, podem ser citadas: melhor representação do comportamento estrutural de edifícios altos; possibilidade de redução do número de paredes estruturais, assim como a adoção de bloco com menor resistência à compressão.

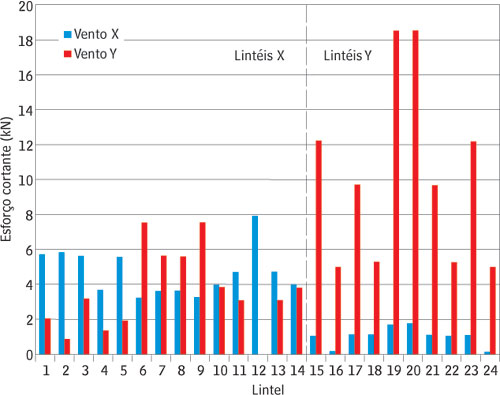
Figura 9 - Esforços cortantes máximos nos lintéis

Efeitos do vento sobre edifícios de alvenaria estrutural

Modelo teórico para análise

Validação do modelo teórico

Edifício exemplo

Comentários finais

Leia Mais