CRV – Sapatas e Tubulões
Para considerar a influência do solo junto à fundação, usou-se a hipótese de Winkler, onde se estabelece que as pressões aplicadas sejam proporcionais, em uma relação escalar, ao recalque mobilizado. Não havendo influência entre o ponto de aplicação desta pressão com sua vizinhança.
Considerando esta hipótese, estabelece uma relação discreta (pontual) entre fundação-solo, mediante a definição de uma constante de mola que representará a rigidez do maciço. Para isto, é necessário definir o valor de Kv o qual é denominado de Coeficiente de Reação Vertical (CRV). Este é um valor escalar que representa o coeficiente de rigidez que o solo possui para resistir ao deslocamento mobilizado por uma pressão imposta. Ele é análogo ao coeficiente de mola, mas não relacionado a uma força, mas sim a uma pressão (força por área), de acordo com o exemplo esquemático na figura 1:
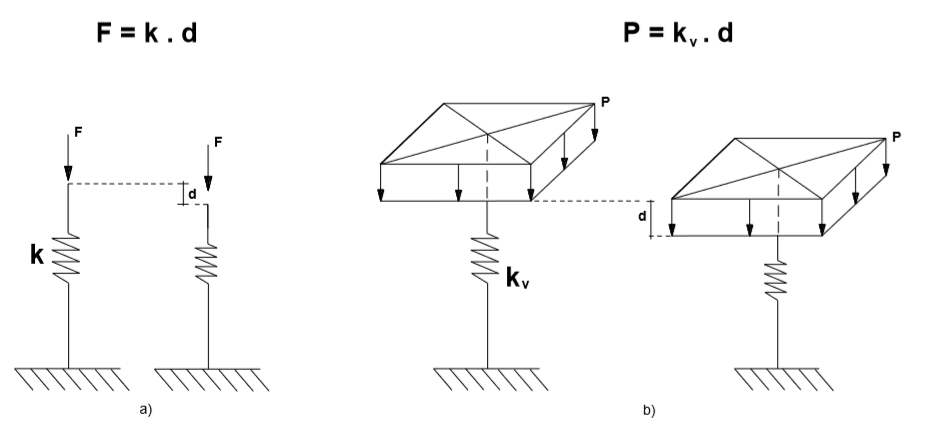
Figura 5.1
a) coeficiente de mola, quociente entre força – deslocamento;
b) coeficiente de reação vertical, quociente entre pressão – deslocamento.
Neste sentido, este texto descreve vários métodos, os quais foram implementados no SISEs, para obtenção deste coeficiente. Ele pode ser obtido por três diferentes maneiras: 1) Valores padronizados; 2) Ensaio de Placa; e 3) Recalque vertical estimado.
A seguir, são definidas e apresentadas cada uma dessas categorias, bem como seus métodos e particularidades, que foram implementados no SISEs.
Métodos Implementados
Os métodos implementados no SISEs para a determinação do coeficiente de reação vertical (CRV) do solo são:
1. VALORES PADRONIZADOS (VP)
Vários pesquisadores apresentam tabelas e ábacos que relacionam o módulo de reação vertical com o tipo de solo. Estes valores foram obtidos em ensaios in situ em regiões e condições específicas, conforme podem ser averiguados nas referências bibliográficas indicadas. Assim, os seus valores podem não ser representativos em certas condições, devendo ficar a critério do profissional o seu uso. Foram considerados três métodos nesta categoria, os quais são:
1.a) Tipo de Solo;
1.b) SPT – Tensão Admissível;
1.c) Tipo de Solo - Tensão Admissível.
2. ENSAIO DE PLACA (EP)
São chamados também de métodos racionais, onde os parâmetros de deformabilidade são obtidos in situ ou em laboratórios mediante o ensaio de provas de carga ensaios mais conhecidos são os apresentados nas tabelas de:
2.a) Terzaghi;
2.b) Outros autores.
3. RECALQUE VERTICAL ESTIMADO (RE)
De acordo com a definição de módulo de reação vertical, que pode ser escrito como:
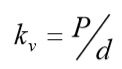
é possível estimar o coeficiente vertical (Kv) a partir do cálculo do recalque da fundação sobre o maciço mobilizado por uma pressão unitária. Os métodos desenvolvidos então nesta categoria foram:
3.a) Teoria da Elasticidade / Valor Típico;
3.b) Teoria da Elasticidade / Schmertmann;
3.c) Teoria da Elasticidade / Teixeira & Godoy;
3.d) Método de Schultze & Sherif;
3.e) Método de Parry;
) Método de Boussinesq;
3.g) Método de Rausch & Cestelli Guidi;
3.h) Módulo Edométrico – Tabelas;
3.i) Módulo Edométrico – SPT.
Valores Padronizados
Tipo de Solo
Neste método, os valores do coeficiente de reação vertical (Kv), em F/L³, são relacionados ao tipo de solo indicados na Tabela de Béton – Kalender de 1962, vide Tabela 5.1.
Referência bibliográfica: MORAES (1981).
| Valores de Kv (em kgf/cm³) | |
| Turva leve-solo pantanoso | 1,0 |
| Turva pesada-solo pantanoso | 1,5 |
| Areia fina de praia | 1,5 |
| Aterro de silte, areia e cascalho | 2,0 |
| Argila molhada | 3,0 |
| Argila úmida | 5,0 |
| Argila seca | 8,0 |
| Argila seca endurecida | 10,0 |
| Silte compactado com areia e pedra | 10,0 |
| Silte compactado com areia e muita pedra | 12,0 |
| Cascalho miúdo com areia fina | 12,0 |
| Cascalho médio com areia fina | 12,0 |
| Cascalho grosso com areia grossa | 15,0 |
| Cascalho grosso com pouca areia | 20,0 |
| Cascalho grosso com pouca areia compactada | 25,0 |
Tabela 5.1 – Valores de Kv da tabela de Béton – Kalender
SPT – Tensão Admissível
Neste método, obtêm-se a média dos valores do SPT compreendidos dentro do bulbo de pressões, vide Figura 5.2. Nesta figura, o escalar “cte” é a profundidade para determinar o bulbo de pressão, e é indicado no arquivo de critérios de projeto ou no editor de fundações que pode variar de 3. Com o valor do número de golpes médio, calcula-se a tensão admissível pela conhecida relação empírica:

Com as tensões admissíveis estimadas, retira-se da tabela SAFE, MORRISON (1993), o valor de Kv em kgf/cm³, Tabela 5.2.2.
Referência bibliográfica: MORRISON (1993).
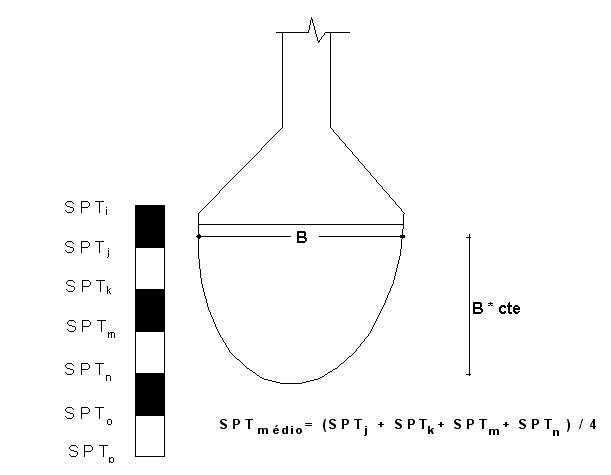
Figura 5.2 – Exemplificação do cálculo do valor médio do SPT dentro do bulbo de pressões.
| Tensão Admissível (kgf/cm²) | Kv (kgf/cm³) | Tensão Admissível (kgf/cm²) | Kv (kgf/cm³) |
| 0,25 | 0,65 | 2,15 | 4,3 |
| 0,30 | 0,78 | 2,20 | 4,4 |
| 0,35 | 0,91 | 2,25 | 4,5 |
| 0,40 | 1,04 | 2,30 | 4,6 |
| 0,45 | 1,17 | 2,35 | 4,7 |
| 0,50 | 1,30 | 2,40 | 4,8 |
| 0,55 | 1,39 | 2,45 | 4,9 |
| 0,60 | 1,48 | 2,50 | 5,0 |
| 0,65 | 1,57 | 2,55 | 5,1 |
| 0,70 | 1,66 | 2,60 | 5,2 |
| 0,75 | 1,75 | 2,65 | 5,3 |
| 0,80 | 1,84 | 2,70 | 5,4 |
| 0,85 | 1,93 | 2,75 | 5,5 |
| 0,90 | 2,02 | 2,80 | 5,6 |
| 0,95 | 2,11 | 2,85 | 5,7 |
| 1,00 | 2,2 | 2,90 | 5,8 |
| 1,05 | 2,29 | 2,95 | 5,9 |
| 1,10 | 2,38 | 3,00 | 6,0 |
| 1,15 | 2,47 | 3,05 | 6,1 |
| 1,20 | 2,56 | 3,10 | 6,2 |
| 1,25 | 2,65 | 3,15 | 6,3 |
| 1,30 | 2,74 | 3,20 | 6,4 |
| 1,35 | 2,83 | 3,25 | 6,5 |
| 1,40 | 2,92 | 3,30 | 6,6 |
| 1,45 | 3,01 | 3,35 | 6,7 |
| 1,50 | 3,10 | 3,40 | 6,8 |
| 1,55 | 3,19 | 3,45 | 6,9 |
| 1,60 | 3,28 | 3,50 | 7,0 |
| 1,65 | 3,37 | 3,55 | 7,1 |
| 1,70 | 3,46 | 3,60 | 7,2 |
| 1,75 | 3,55 | 3,65 | 7,3 |
| 1,80 | 3,64 | 3,70 | 7,4 |
| 1,85 | 3,73 | 3,75 | 7,5 |
| 1,90 | 3,82 | 3,80 | 7,6 |
| 1,95 | 3,91 | 3,85 | 7,7 |
| 2,00 | 4,0 | 3,90 | 7,8 |
| 2,05 | 4,1 | 3,95 | 7,9 |
| 2,10 | 4,2 | 4,0 | 8,0 |
Tabela 5.2.2 - Valores para Kv ; SAFE, MORRISON (1993)
Como limitou o intervalo de SPT entre 1 e 40, o Sises aplica uma aproximação linear para valores de tensão que estejam fora dessa tabela 5.2.2 de Morrison (1993).
Tipo de Solo – Tensão Admissível
Neste método, em função do tipo de solo da camada, retira-se o valor da tensão básica conforme apresentado na Tabela 4 da NBR 6122:1996, ou na Tabela 5.3, fazendo as correções de profundidade e de geometria conforme preconiza esta mesma norma para solos granulares e argilosos.
Com as tensões admissíveis estimadas, retira-se da tabela SAFE, MORRISON (1993), o valor de Kv em kgf/cm³.
A tabela seguir, que relaciona a descrição do solo e sua tensão admissível, é reproduzida no SISEs, item arquivo de critérios. Duas novas linhas são adicionadas a esta tabela, linhas referentes ao item “Conforme SPT” para areia e argila que, em função da cota de assentamento da fundação e de seu respectivo valor de SPT, busca – para cada caso de areia e/ou argila – a sua classificação de consistência e compacidade conforme a tabela 7.1 e o valor da tensão admissível.
Referência bibliográfica: CINTRA et al. (2003), MORRISON (1993).
| Descrição do tipo de solo ** | |
| Rocha sã, maciça, sem laminação | 3,0 |
| Rocha laminada, com pequenas fissuras | 1,5 |
| Solos granulares concrecionados, conglomerados | 1,0 |
| Pedregulho fofo | 0,3 |
| Pedregulho compacto a muito compacto | 0,6 |
| Argila dura (SPT >19) | 0,3 |
Argila média (6 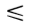 SPT SPT 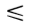 10) 10) | 0,1 |
Argila rija (11 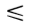 SPT SPT 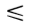 19) 19) | 0,2 |
| Areia muito compacta (SPT >40) | 0,5 |
Areia compacta (19 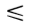 SPT SPT 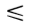 40) 40) | 0,4 |
Areia med. compacta (9 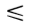 SPT SPT 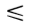 18) 18) | 0,2 |
| Silte muito compacto (ou duros) | 0,3 |
| Silte compactos (ou rijos) | 0,3 |
| Silte médio (medianamente compacto) | 0,1 |
** valores válidos para largura de , em outros casos deve-se fazer correção
Tabela 5.3 – Valores das Tensões básicas (NBR 6122:1996)
Os valores da tabela de tensões básicas devem ser modificados em função das dimensões e da profundidade do elemento de fundação, além do tipo de solo, conforme prescrições da NBR 6122:1996.
i) Prescrição Especial para Solos Granulares
Se solo abaixo até 2 vezes a largura da cota de apoio do elemento de fundação é do tipo (solo granular e areias), corrige-se a tensão básica em função de sua largura (B), de duas maneiras:
1 - Construções não sensíveis a recalques,
Realiza-se uma redução proporcional à menor largura da fundação, com o uso da expressão:
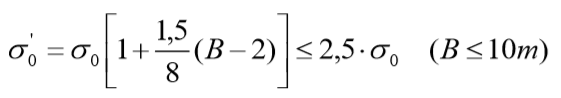
2 - Construções sensíveis a recalques:
Caso B > 2m, a NBR 6122/96 recomenda fazer uma verificação dos eventuais efeitos de recalques. Não se corrige as tensões básicas.
Caso B < 2m, emprega-se a redução proporcional indicada em “Construções não sensíveis a recalques”.
Dentro do SISEs, no arquivo de critérios de projeto, é possível definir se a construção é sensível ou não a recalques, conforme indicação do usuário (default: é sensível a recalque).
ii) Prescrição Especial para Solos Argilosos
Para solos que sejam argilosos (conforme definido pelo usuário em sondagem), devem-se reduzir os valores da tabela com a expressão:
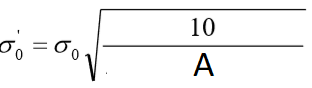
A: área da fundação (A![]() 10m²)
10m²)
Esta redução pode ser rigorosa em alguns casos, e no SISEs, seguindo recomendações indicadas na versão anterior da norma de Fundações, caso este valor reduzido seja menor que a metade do valor da tabela, usa este último como redução:

Resumo dos Diversos Métodos –Valores Padronizados
Abaixo é apresentada uma tabela resumindo os diversos métodos para cálculo do Coeficiente de Reação Vertical com algumas características importantes de cada um, tais como: consideração de camadas, propagação de tensões, associação de camadas, grau de dependência do SPT, etc. Esta tabela tem o objetivo de auxiliar a seleção do método desejado e apresentar o número de variáveis a serem definidas na associação às camadas da sondagem.
| Método para calculo doCRV | Tipo Solo | ConsideraDiversasCamadas? | Propaga-ção deTensões | Associa-çãoCamadaSonda-gempelo SPT | Associa-ção CamadaSonda-gempelo Titulo | Variáve-is a definirporcamada | Depen-dência doMétodo/ SPT |
| Tipo de Solo | Qquer | Não | Não | Não | Sim | CRV | Nenhum |
| SPT – TensãoAdmissível | Qquer | Sim-Bulbo | Não | Sim | Não | --- | Total |
| Tipo do SoloTensão Admissível | Qquer | Não | Não | Não | Sim | T.Adm. | Nenhum |
| AreiaArgila | Não | Não | Sim | Não | T.Adm. | Parcial |
Ensaio de Placa
Tabela de TERZAGHI
Neste método, os valores de Kv (kgf/cm³) são relacionados ao tipo de solo fornecido por TERZAGHI (1955) e indicados na Tabela 5.4. Estes valores foram obtidos no ensaio de uma placa quadrada de lado um pé (30 cm), por isso indicados por k30. Deve ser então corrigido para considerar o efeito de dimensão e forma, conforme indicação nas relações abaixo:
Para argilas:
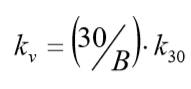
Para areias:
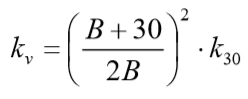
onde B é o lado menor da sapata, em centímetros.
Referência bibliográfica: VELLOSO & LOPES (1996), TERZAGHI (1955).
| Argila | Rija | Muito rija | Dura |
| faixas de valores | 1,6 – 3,2 | 3,2 – 6,4 | > 6,4 |
| valores propostos | 2,4 | 4,8 | 9,6 |
| Areia | Fofa | Med. compacta | Compacta |
| acima do NA | 1,3 | 4,2 | 16 |
| abaixo do NA | 0,8 | 2,6 | 9,6 |
Tabela 5.4 – Valores de k30 da tabela TERZAGHI (kgf/cm³)
Tabela de Outros Autores
Neste método, os valores de Kv (kgf/cm³) propostos por outros autores são relacionados ao tipo de solo. Os valores de k30 são apresentados na Tabela 5.5 e também devem ser corrigidos conforme as expressões do método 5.3.1:
| Descrição do tipo de solo | k30 (kgf/cm³) |
| Areia fina de praia | 1,5 |
| Areia fofa seca úmida | 3,0 |
| Areia média seca úmida | 9,0 |
| Areia compacta seca úmida | 20,0 |
| Areia pedregulhosa fofa | 8,0 |
| Areia pedregulhosa compacta | 25,0 |
| Pedregulho arenoso fofo | 12,0 |
| Pedregulho arenoso compacto | 30,0 |
| Rochas brandas ou alteradas (saprólito) | 500,0 |
| Rocha sã | 30.000 |
Tabela 5.5 – Valores de k30 propostos por outros autores
Referência bibliográfica: ACI (1988), CALAVERA (2000), BOWLES (1997).
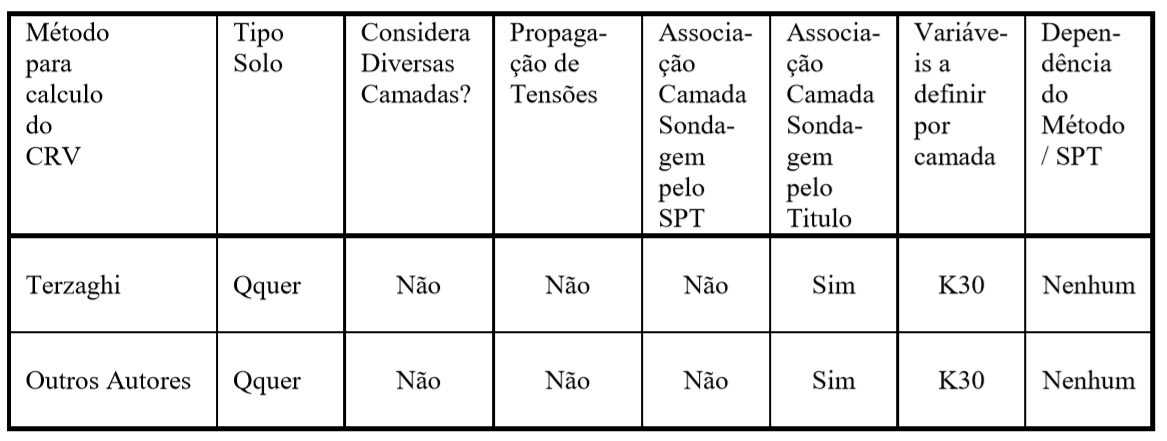
Resumo dos Diversos Métodos – Ensaios de Placas
Abaixo é apresentada uma tabela resumindo os diversos métodos para cálculo do Coeficiente de Reação Vertical com algumas características importantes de cada um, tais como: consideração de camadas, propagação de tensões, associação de camadas, grau de dependência do SPT, etc. Esta tabela tem o objetivo de auxiliar a seleção do método desejado e apresentar o número de variáveis a serem definidas na associação às camadas da sondagem.
Recalque Vertical Estimado
Teoria da Elasticidade / Valor Típico
Nesta opção, empregam-se as expressões analíticas de MINDLIN, indicadas em POULOS & DAVIS (1974), que são as respostas exatas de deslocamentos (d) dentro do meio contínuo semi-infinito homogêneo para um dado carregamento. No caso de se simular o meio heterogêneo e com o plano do indeslocável em uma posição conhecida, Figura 5.3b, usa-se o procedimento de STEINBRENNER, POULOS (1967), o qual é descrito no item 11 desse manual. Para isto é necessário conhecer o módulo de elasticidade e o coeficiente de Poisson do solo em cada camada.
O módulo de elasticidade é obtido conforme os valores sugeridos pela tabela 5.6. O coeficiente de Poisson do solo é indicado na tabela 5.7, valores sugeridos por TEIXEIRA & GODOY (1996).
Referência bibliográfica: TEIXEIRA & GODOY (1996), POULOS & DAVIS (1974), POULOS (1967).
| Descrição do tipo de solo | E (kgf/cm²) |
| Argila conforme SPT | * |
| Areia conforme SPT | * |
| Areia normal adensada | E = 5 (SPT+5) |
| Areia sobreadensada | E = 180+(7,5.SPT) |
| Argila terciária de SP | E = 55,4+(25,9.SPT) |
| Areia fofa (SPT ≤ 4) | 50 |
| Areia pouco compacta (SPT 5 a 8) | 200 |
| Areia medianamente compacta (SPT 9 a 18) | 500 |
| Areia compacta (SPT 19 a 40) | 700 |
| Areia muito compacta (SPT > 40) | 900 |
| Argila muito mole (SPT ≤ 2) | 10 |
| Argila mole (SPT 2 a 5) | 20 |
| Argila média (SPT 6 a10) | 50 |
| Argila rija (SPT 11 a 19) | 80 |
| Argila dura (SPT > 19) | 150 |
Tabela 5.6 – Valores típicos para o módulo de elasticidade do solo
| Descrição do tipo de solo | |
| Argila conforme SPT | * |
| Areia conforme SPT | * |
| Areia fofa (SPT ≤ 4) | 0,35 |
| Areia pouco compacta (SPT 5 a 8) | 0,35 |
| Areia medianamente compacta (SPT 18) | 0,35 |
| Areia compacta (SPT 19 a 40) | 0,35 |
| Areia muito compacta (SPT > 40) | 0,35 |
| Argila muito mole (SPT ≤ 2) | 0,3 |
| Argila mole (SPT 2 a 5) | 0,3 |
| Argila média (SPT 6 a 10) | 0,3 |
| Argila rija (SPT 11 a 19) | 0,3 |
| Argila dura (SPT > 19) | 0,3 |
Tabela 5.7 – Valores sugeridos para o coeficiente de Poisson do solo
O recalque (d) abaixo do vértice de uma área retangular carregada com carga uniformemente constante - Figura 5.3a - é dado pela equação indicada em Poulos & Davis (1974), descrita a seguir:
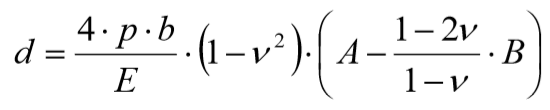
Onde:
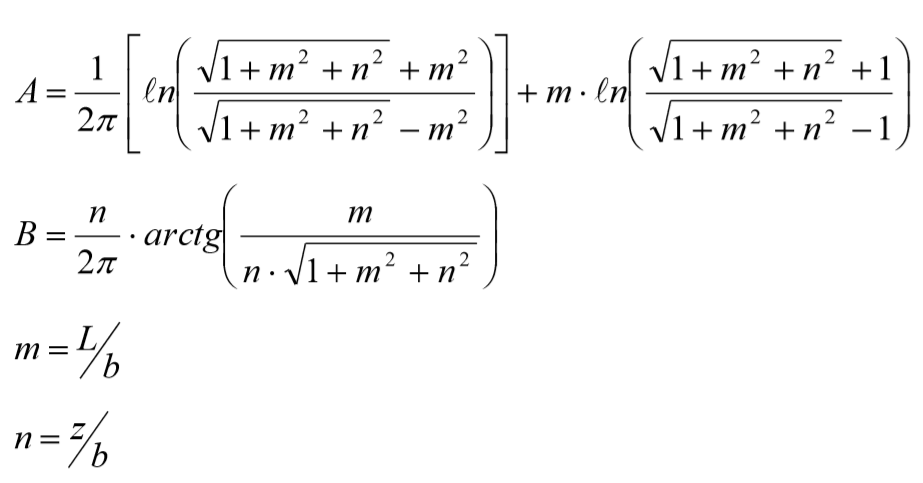
Com
p: carga uniformemente distribuída, no SISEs; p = 1 kgf/cm² ;
b: menor largura da fundação;
L: maior comprimento da fundação;
E: módulo de elasticidade;
: coeficiente de Poisson;
d: recalque calculado
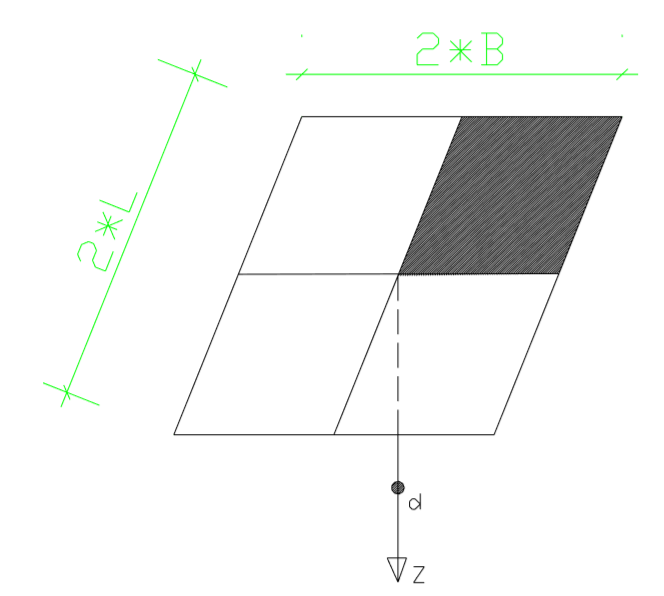
Figura 5.3a – Localização e variáveis para cálculo do recalque de uma área retangular.
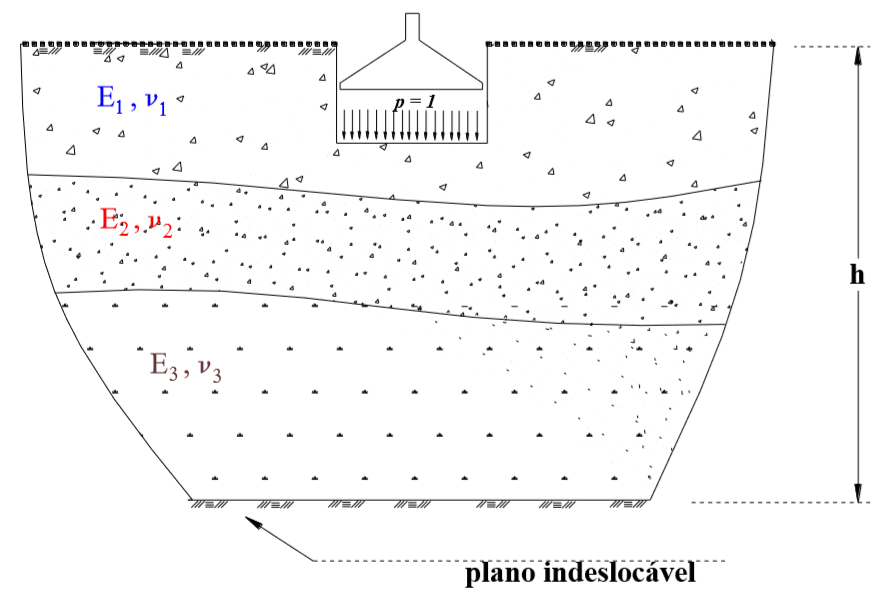
Figura 5.3b – Maciço de solos heterogêneo e com plano indeslocável a distância h.
Teoria da Elasticidade / Schmertmann
Este método utiliza a mesma formulação do item 5.4.1, empregando também o procedimento de Steinbrenner. Mas o módulo de elasticidade é obtido conforme proposto por SCHMERTMANN (1978), sendo dado pela relação:
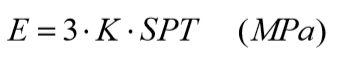
onde K depende do tipo de solo. Na Tabela 5.8 são apresentados seus valores típicos propostos por TEIXEIRA (1993):
| Descrição do tipo de solo | K (MPa) |
| Areia com pedregulhos | 1,10 |
| Areia | 0,90 |
| Areia Siltosa | 0,70 |
| Areia argilosa | 0,55 |
| Silte arenoso | 0,45 |
| Silte | 0,35 |
| Argila arenosa | 0,30 |
| Silte argiloso | 0,25 |
| Argila siltosa | 0,20 |
Tabela 5.8 – Valores sugeridos de K
Referência bibliográfica: CINTRA et al. (2003), SCHMERTMANN (1978), TEIXEIRA (1993).
Teoria da Elasticidade / TEIXEIRA & GODOY
Este método utiliza a mesma formulação do item 5.4.1, empregando também o procedimento de Steinbrenner. Mas o módulo de elasticidade é obtido conforme proposto por TEIXIERA & GODOY (1996) que estabelece a seguinte relação para fundações diretas:
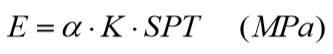
onde é um coeficiente que correlaciona a resistência de ponta (qc) com o SPT. Seus valores para a areia e argila foram propostos por TROFIMENKOV (1974) e são apresentados na Tabela 5.9. O coeficiente K é o mesmo utilizado no item 5.4.2 e apresentado na Tabela 5.8.
| Descrição do tipo de solo | |
| Areia | 3 |
| Silte | 5 |
| Argila | 7 |
Tabela 5.9 – Valores sugeridos de .
Referência bibliográfica: CINTRA et al. (2003), SCHMERTMANN (1978), TEIXEIRA (1993).
Método de SCHULTZE & SHERIF
Este modelo é utilizado para a estimativa de recalques em solos arenosos, sendo a expressão utilizada para o cálculo do valor deste recalque dada por:
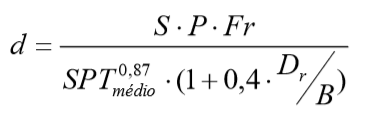
Com:
d – recalque vertical (cm);
S – o coeficiente de recalque (cm³/kgf), conforme Figura 5.4;
Dr – profundidade da fundação (m);
B – largura da fundação (m);
P – pressão aplicada pela fundação sobre o solo (kgf/cm²);
SPTmédio – valor médio obtido conforme descrito e exemplificado na Figura 5.2;
Fr – fator de redução, conforme Tabela 5.10;
DS – espessura entre a cota de assentamento da fundação e a cota do indeslocável (m);
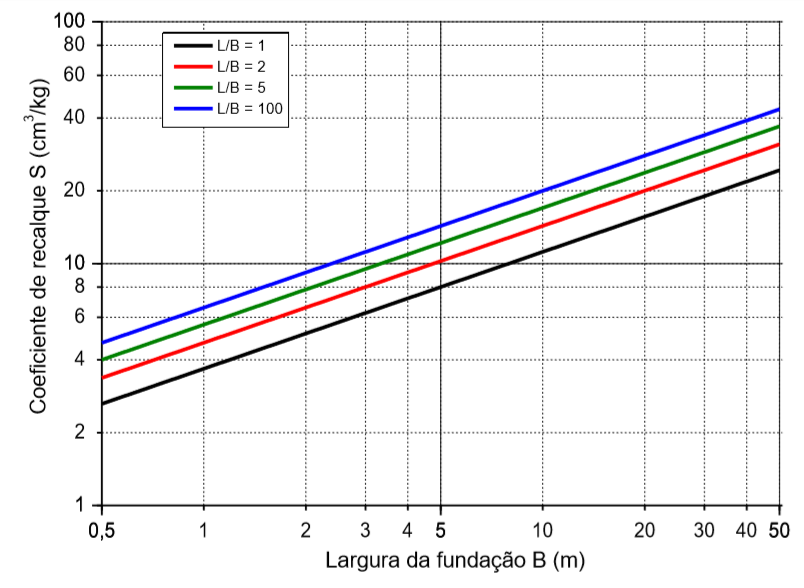
Figura 5.4 – Relação entre o coeficiente de recalque versus largura da fundação do método de Schultze & Sherif.
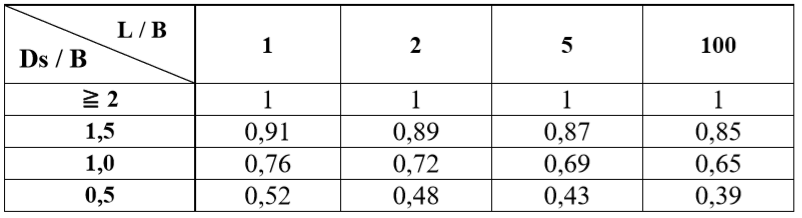
Tabela 5.10 – Valores dos fatores de redução - Fr
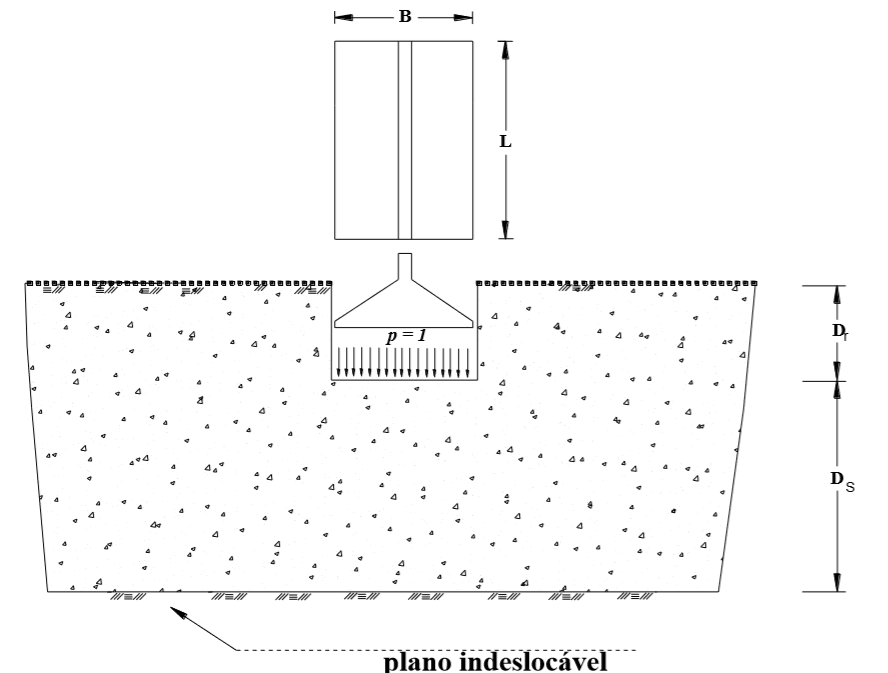
Figura 5.5 – Definição dos parâmetros empregados no método de SCHULTZE & SHERIF.
Referência bibliográfica: SCHULTZE & SHERIF (1973), MOURA (1995).
Método de PARRY
Este modelo é utilizado para a estimativa de recalques em solos arenosos, sendo a expressão utilizada para o cálculo do valor deste recalque dada por:
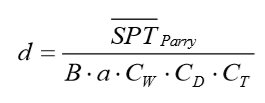
Com:
d – recalque vertical (m);
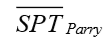 – valor médio do SPT;
– valor médio do SPT;
B – largura da fundação (m), vide Figura 5.6;
a – constante igual a 3x10– 4 ( m²/kN);
CD – coeficiente de influência da profundidade, vide figura 5.7;
CT – coeficiente de correção da espessura da camada compressível, vide Figura 5.8;
CW – coeficiente de correção da influência do lençol freático, veja relações a seguir.
O valor de 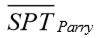 é obtido mediante o emprego da seguinte relação:
é obtido mediante o emprego da seguinte relação:
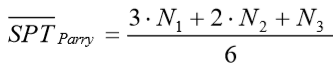
onde se deve considerar os valores de N1, N2 e N3 conforme esquematizado na Figura 5.9.
Os valores de CW são dados de acordo com as expressões abaixo:
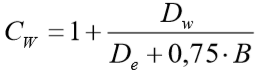
quando 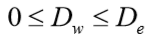
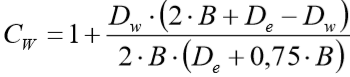
quando 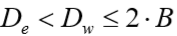
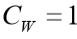
quando 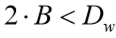
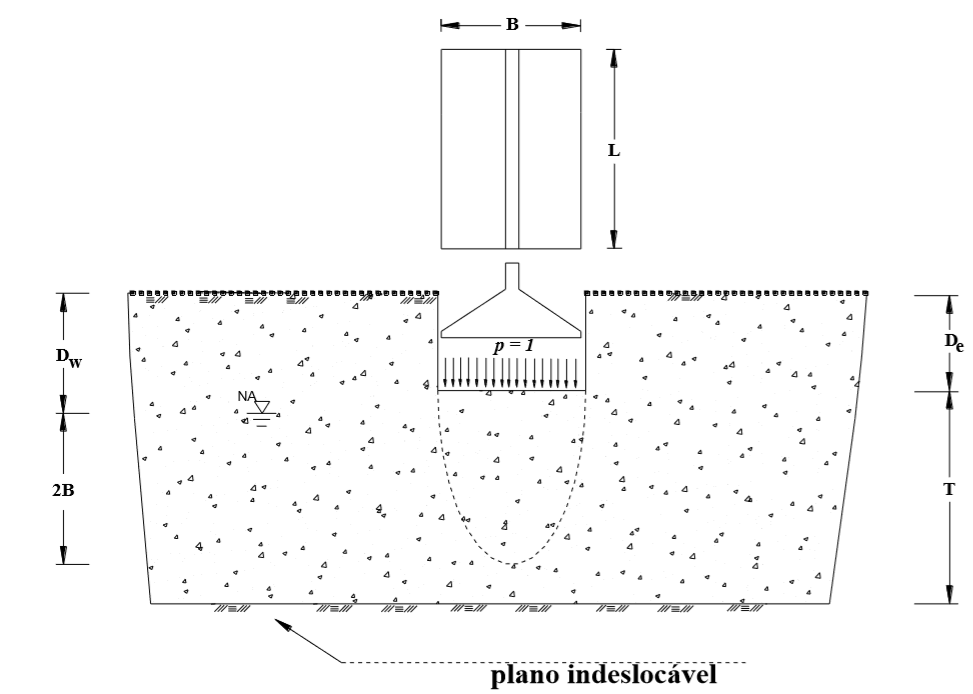
Figura 5.6 – Definição dos parâmetros empregados no método de Parry.

Figura 5.7 – Coeficiente de influência da profundidade, PARRY (1971).

Figura 5.8 – Coeficiente de correção da espessura da camada compressível, PARRY (1971).
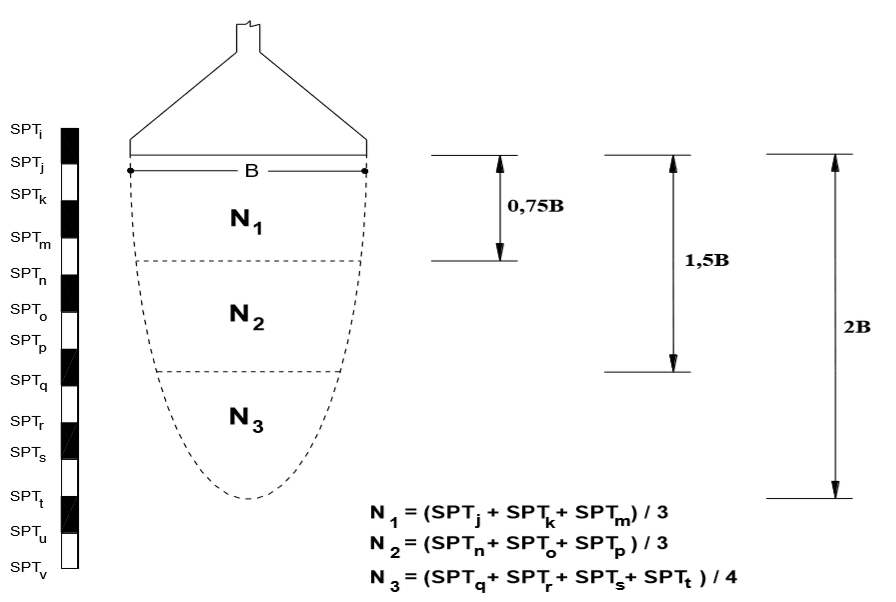
Figura 5.9 – Exemplificação do cálculo do valor médio do SPT dentro do bulbo de pressões para o método de PARRY.
Referência bibliográfica: PARRY (1971), PARRY (1978), MOURA (1995).
Método de BOUSSINESQ
Neste método, calcula-se o recalque do meio elástico mediante a expressão de BOUSSINESQ, aplicada a uma placa circular admitida rígida e submetida a uma pressão constante. A relação é dada por:
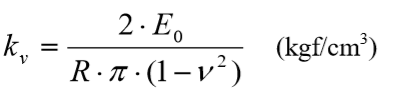
Com:
E0 : módulo edométrico do solo, obtido conforme a tabela 5.11;
R: raio da placa de fundação, para as fundações retangulares, usou-se um raio equivalente (cm);
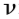 : coeficiente de Poisson, obtido conforme tabela 5.7.
: coeficiente de Poisson, obtido conforme tabela 5.7.
| Descrição do tipo de solo | E0 (kgf/cm²) |
| Turfa | 5 |
| Argila molhada | 40 |
| Argila plástica | 80 |
| Argila endurecida – plástica | 150 |
| Areia solta | 200 |
| Areia compacta | 800 |
Tabela 5.11 – Valores do módulo edométrico sugeridos por CESTELLI GUIDI (Moraes, 1981)
Referência bibliográfica: MORAES (1981).
Método de RAUSCH & CESTELLI GUIDI
Neste método os valores de Kv (kgf/cm3) são obtidos mediante o uso da expressão:
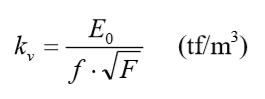
Com:
E0: módulo edométrico do solo, obtido conforme a tabela 5.11;
f: coeficiente adimensional que depende da área da fundação, de valor admitido constante igual a 0,4;
F: área da fundação em m².
Referência bibliográfica: MORAES (1981).
Módulo Edométrico – Tabelas
Neste método, o recalque é estimado com o uso da expressão:
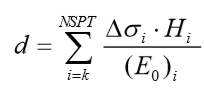
Com:
NSPT: número total de golpes medidos na sondagem;
k: primeira camada subjacente a cota de assentamento da fundação;
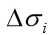 : valor da tensão na cota i que resulta da aplicação da pressão unitária na cota k;
: valor da tensão na cota i que resulta da aplicação da pressão unitária na cota k;
Hi: espessura da camada i, que é igual a 1m;
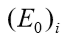 : módulo edométrico da camada i do solo, obtido conforme a tabela 5.11.
: módulo edométrico da camada i do solo, obtido conforme a tabela 5.11.
A expressão acima indica que se deve calcular a contribuição de cada camada para o recalque total. Assim, em função da pressão unitária admitida aplicada na cota de assentamento da fundação, obtêm-se a tensão mobilizada ao longo de todas as camadas subjacentes, bem como o seu módulo edométrico e sua espessura. Admite-se a espessura como a distância entre a medida de um SPT e seu adjacente, ou seja, igual a 1m.
Com a medida final do recalque e admitindo uma pressão unitária aplicada, pode-se chegar ao valor do módulo de reação vertical, usando a definição de Winkler:
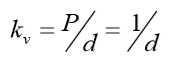
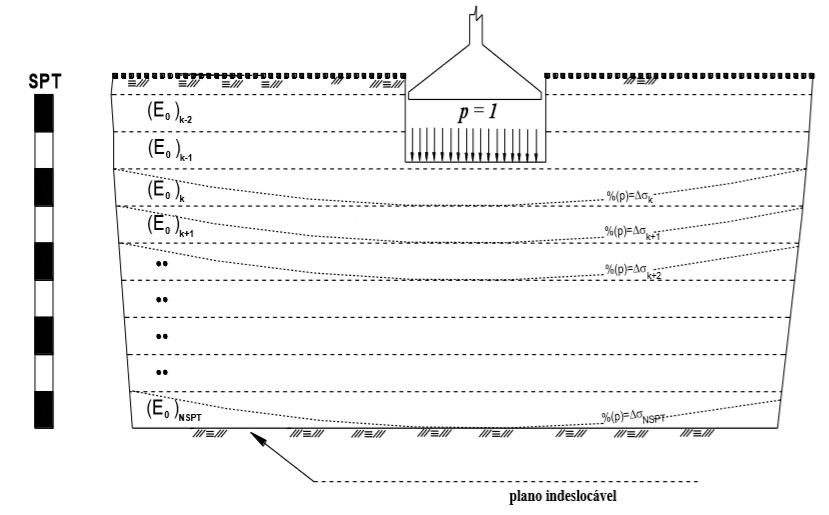
Figura 5.10 – Exemplificação dos parâmetros empregados no método Módulo Edométrico.
É possível fazer a determinação da propagação de tensões ao longo das camadas por três procedimentos, os quais são usados no SISEs:
i) método Simplificado;
ii) método de Boussinesq;
iii) método de Love.
Cada um deles é descrito a seguir.
i) Método Simplificado
A propagação da tensão é feita tomando-se como hipótese um decréscimo linear de seu valor ao longo da profundidade, de razão definida a priori pelo usuário. Assim, seja a Figura 5.11, a tensão aplicada na base da fundação é dada por:
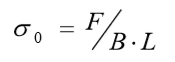
Ao longo da profundidade esta tensão é propagada linearmente, valendo para uma cota genérica z:
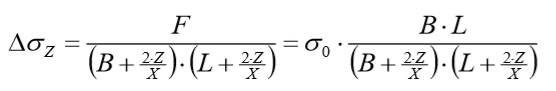
O valor da variável “X” é fornecido no arquivo de critérios de projeto sendo que 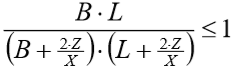 e indica o índice de propagação da tensão ao longo da profundidade.
e indica o índice de propagação da tensão ao longo da profundidade.
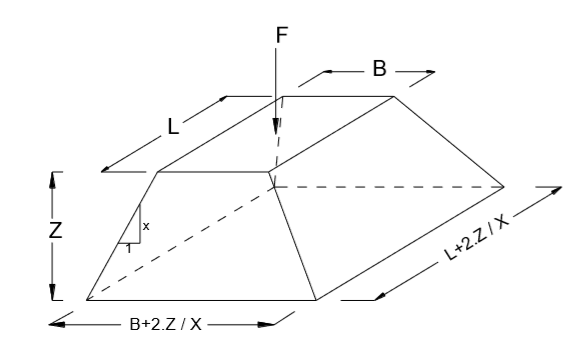
Figura 5.11 – Propagação de tensão com hipótese de decréscimo linear.
ii) Método de Boussinesq
Em BOUSSINESQ (1885) são apresentadas primeiramente as expressões, obtidas via resolução das relações da elasticidade, para cálculo de deslocamentos e tensões dentro de um meio homogêneo, elástico e semi-infinito mobilizados ao se aplicar uma força vertical concentrada na superfície livre deste meio. A partir de então vários autores generalizaram estas expressões, considerando casos como pressões distribuídas em uma área retangular, circular, parabólica, cônico, etc.
Assim, têm-se as expressões de HOLL (1940) que apresenta as relações de tensões e deslocamentos mobilizados no meio em conseqüência de um carregamento vertical, retangular e uniforme aplicado na superfície, conforme exemplificado na Figura 5.12 indicado na expressão abaixo:
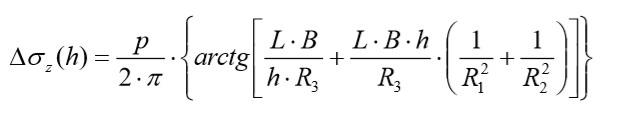
Com:
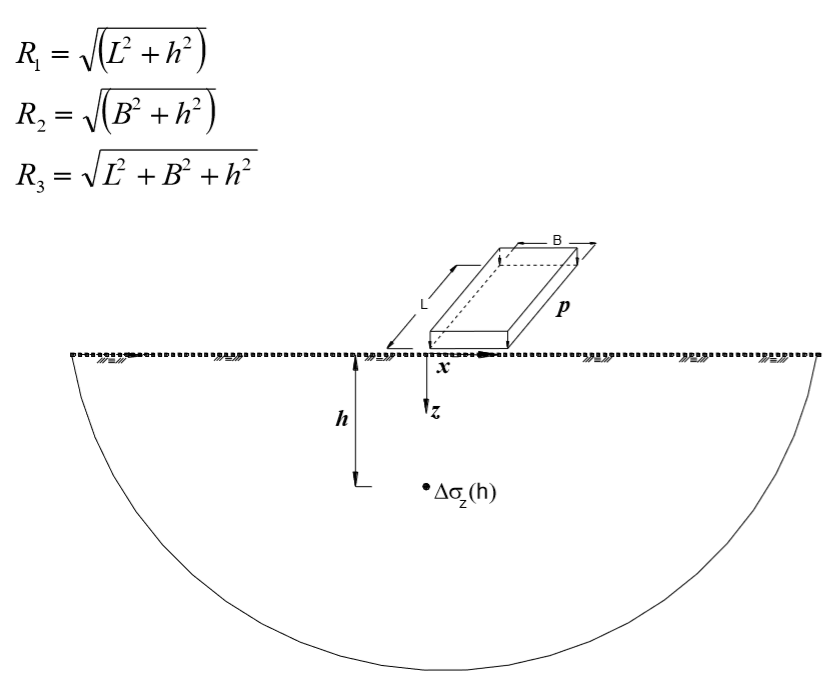
Figura 5.12 – Meio elástico, homogêneo e semi-infinito sujeito a um carregamento vertical, retangular e uniforme.
Referência bibliográfica: BOUSSINESQ (1885), HOLL (1940), POULOS & DAVIS (1974).
iii) Método de Love
LOVE (1945) apresentou as relações obtidas pela teoria da elasticidade, também derivadas de BOUSSINESQ (1885), para o caso da aplicação de um carregamento vertical, circular e uniforme, onde a expressão para a tensão na direção z é dada por:
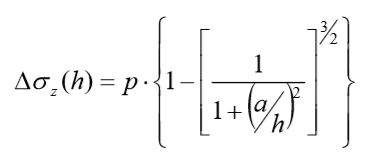
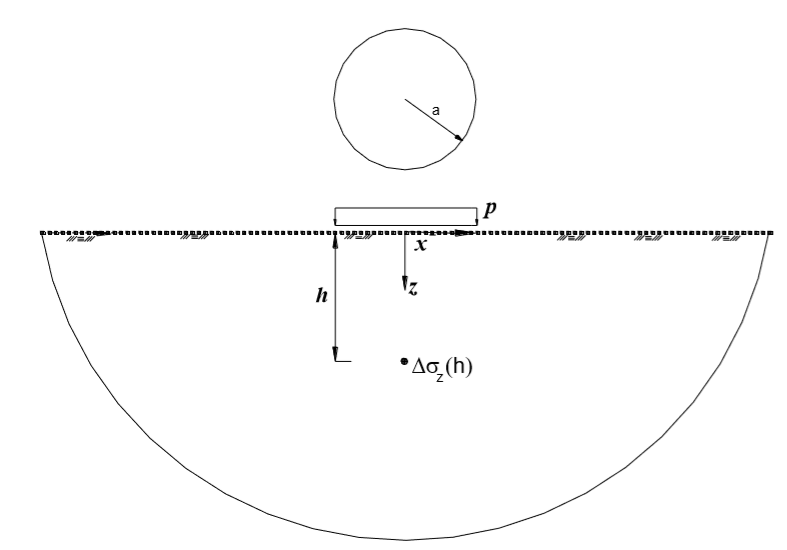
Figura 5.13 – Meio elástico, homogêneo e semi-infinito sujeito a um carregamento vertical, circular e uniforme.
Módulo Edométrico – SPT
Este método é similar ao apresentado no item 5.4.8, mas o módulo edométrico é calculado mediante uma correlação com o número de golpes, o SPT, o qual fora proposto por SCHULTZE & MENZENBACH (1961). A relação é dada por:
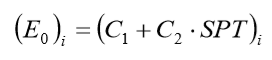
onde i é uma camada genérica do maciço. As constantes C1 e C2 são indicadas na tabela 5.12.
| Descrição do tipo de solo | C1 | C2 |
| Areia fina abaixo do lençol de água | 71 | 4,9 |
| Areia fina acima do lençol de água | 52 | 3,3 |
| Areia | 39 | 4,5 |
| Areia argilosa | 43,8 | 11,8 |
| Areia e argila | 38 | 10,5 |
| Areia fofa | 24 | 5,3 |
Tabela 5.12 – Constantes (bar/golpe) usadas na determinação do módulo edométrico mediante o SPT
Referência bibliográfica: SCHULTZE & MENZENBACH (1961).
Resumo dos Diversos Métodos – Recalque Vertical
Abaixo é apresentada uma tabela resumindo os diversos métodos para cálculo do Coeficiente de Reação Vertical com algumas características importantes de cada um, tais como: consideração de camadas, propagação de tensões, associação de camadas, grau de dependência do SPT, etc. Esta tabela tem o objetivo de auxiliar a seleção do método desejado e apresentar o número de variáveis a serem definidas na associação às camadas da sondagem.
| Método para cálculo do CRV | Tipo Solo | Considera Diversas Camadas? | Propagação de Tensões | Associa-ção Camada Sondagem pelo SPT | Associação Camada Sondagem pelo Titulo | Variáveis a definir por camada | Dependência do Método / SPT |
| Elasticidade Valor Típico | Areia Argila | Sim-St/Po | Não | Sim | Não | --- | Total |
| Areia Argila Outro | Sim-St/Po | Não | Não | Sim | E, Ni | Nenhum | |
| Elasticidade Schmertmann | Qquer | Sim-St/Po | Não | Sim | Sim | K e Ni | Parcial |
| Elasticidade Teixeira Godoy | Qquer | Sim-St/Po | Não | Sim | Sim | Alfa, KNi | Parcial |
| Schultze &Sherif | Areia | Sim-Bulbo | Não | Sim | Não | --- | Total |
| Parry | Areia | Sim-Bulbo | Não | Sim | Não | --- | Total |
| Boussinesq | Qquer | Não | Não | Não | Sim | Eo e Ni | Nenhum |
| Rausch & Cestelli Guidi | Qquer | Não | Não | Não | Sim | Eo | Nenhum |
| Módulo Edométrico Tabelas | Qquer | Sim | Sim | Não | Sim | Eo | Nenhum |
| Módulo EdométricoSPT | Qquer | Sim | Sim | Sim | Sim | C1 e C2 | Parcial |
St/Po: Recalque através de proposição por Steinbrenner, Poulos (1967)
