Correções sobre CRV e tensão em sapatas

As tensões atuantes em cada elemento de fundação superficial (sapatas/radiers) não possuem uma distribuição constante para as fundações flexíveis, conforme indicado pelas referências de TEIXEIRA & GODOY (1996), VELLOSO & LOPES (1996) e esquematizados na Figura 7.1. Dessa forma, para simular essa distribuição não constante entre fundação/solo, desenvolveram-se duas metodologias para simular esse efeito.

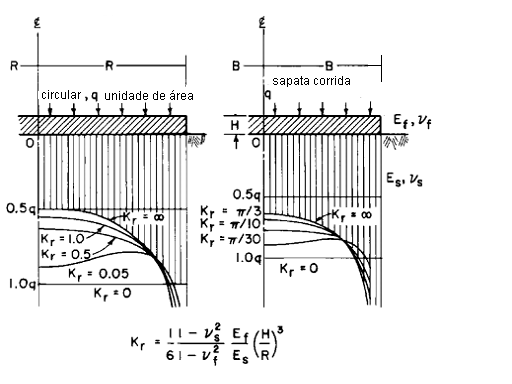
83220524282b34d69686449c0c4fa1b7.png


Figura 7.1 - Pressão de contato para fundação flexível – Adap. de Borowicka (1936, 1938)


A primeira, denominada de ”Modelo de Correção do Coeficiente de Mola”, atua sobre o valor de CRV de elemento de fundação. Assim, independentemente do Método de Cálculo do CRV escolhido, aplica-se um ponderador sobre esse valor, levando a influência do solo variar de ponto a ponto da fundação. Assim, as análises de esforços, recalques e tensões do projeto são realizadas sobre essa configuração.

A segunda, denominada de “Modelo de Pressão de Contato”, realiza a correção de contato entre a fundação/solo sobre as tensões constantes obtidas na análise convencional. Essa correção é realizada em função de características mecânicas e geométricas do conjunto fundação/solo, mediante um fator de rigidez relativo -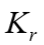797d8feaedf1de84aaa09f1b9e990c3e.png .

Em seguida, são apresentados com mais detalhes os procedimentos de cálculo das tensões de contato fundação/solo desenvolvidos no SISES.


Modelo de Correção do Coeficiente de Mola

Para diversos casos de rigidez relativa entre solo-sapata, se obtém - via Teoria da Elasticidade - valores de deslocamentos para os pontos da sapata, os quais geram uma curva de recalque, a qual é empregada para determinar um coeficiente de rigidez em cada ponto da sapata. Veja exemplo.

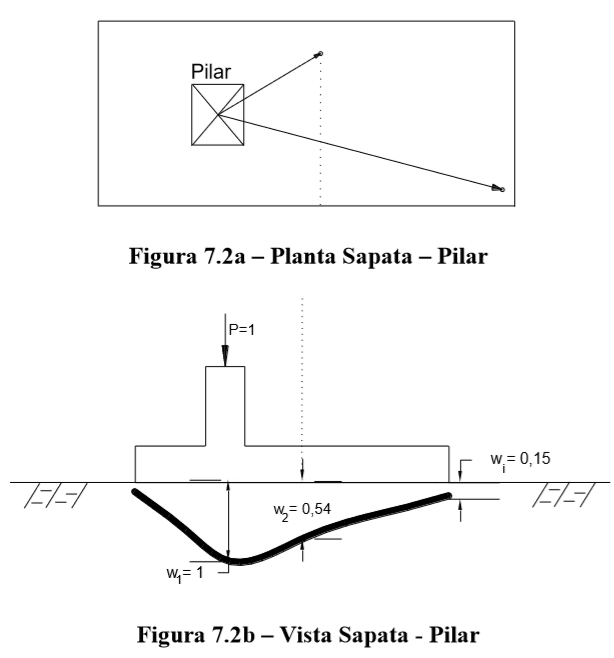
Seja a sapata com um pilar em uma determinada posição, conforme Figura 7.2a. Os deslocamentos calculados (via Teoria da Elasticidade, já considerando a sapata, sua rigidez, geometria, tipo de solo), estão esquematicamente indicados na Figura 7.2b.



d67de20c84867cb3b6c8fb1db3836d58.png


A relação entre recalque (w) e força aplicada (P) é dada pela relação clássica: 332ab47de99a5aac14aaf7df487f2d6b.png

ou para o caso de força unitária: 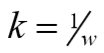1d0503fbc4ca3362d7c942bd9af80518.png

Assim, para os deslocamentos exemplificados e indicados na Figura 7.2b, têm-se os coeficientes de molas, os quais são apresentados na Figura 7.3:

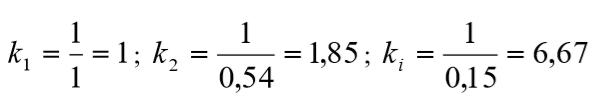
3e87be0d77d8a747a213d4b31fa2c246.png

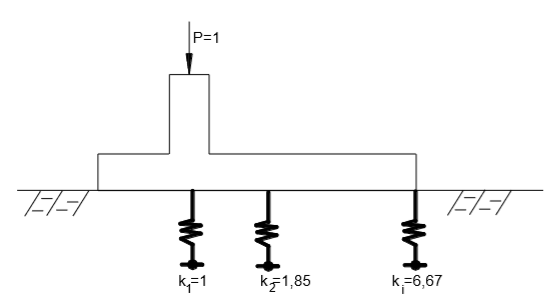
e989af035a149d3eb7a1028d774251d6.png

Figura 7.3 – Valores de mola distintos na mesma sapata

1a137257ff95e372aa514128a8938db2.png

Veja o modelo adotado esquematicamente nas Figuras 7.4a e 7.4b.


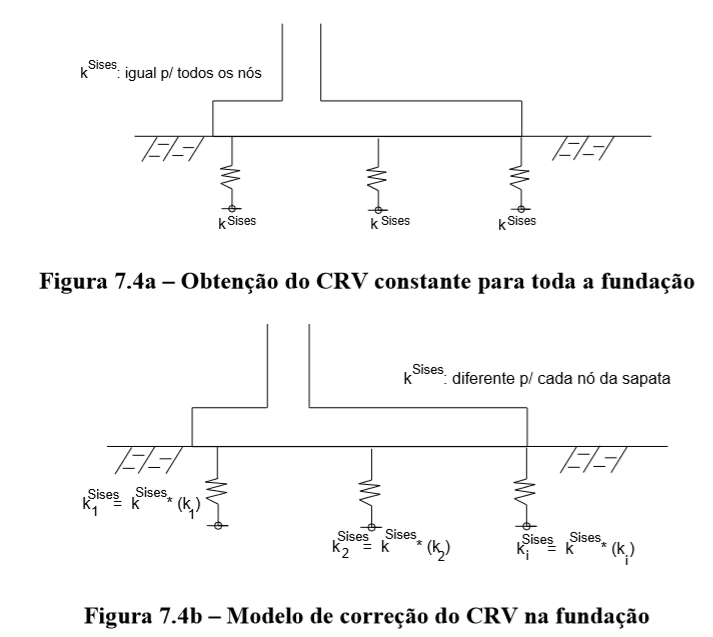
9fde118d1e270dbd4590b50e3f07e4e4.png


A avaliação do recalque fora tomado seguinte modelo da teoria da Elasticidade, de modo a considerar a sapata integrada com o solo homogêneo, seguindo referência de Poulos & Davis (1974).

Estes deslocamentos foram calculados em uma rotina específica para quatro (4) posições do pilar sobre a sapata, indicados na Figura 7.5.


c0c88a422e24cc814f8f969d58d91d78.png


Figura 7.5 – Modelos considerados para posição do pilar na sapata


Foi aproximada então uma curva de ajuste para os quatro (4) casos, de modo que para cada uma destas posições do pilar na sapata, é possível obter o deslocamento de certo ponto qualquer da sapata. Normalizaram-se os deslocamentos para ponderá-los no intervalo de 1.

Isto é feito também para dois (2) casos de geometria de sapata, de comprimento L e largura B: 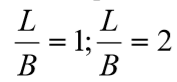0c5c2775e00ca76c51d7500abec6690e.png ; onde se notou que os valores não se alteravam significativamente para outras escalas.

Além das curvas para os diferentes fatores de geometria, também se considerou a relação entre rigidez sapata/solo, com o parâmetro kr dado por:

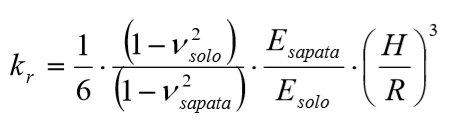
15dc92746afc2ee17c887bf7b0cce6ee.png

Onde se gerou resultados para dois tipos de kr: kr = 1 e kr = 0,05.


Desse modo, com os dados da geometria de cada fundação, das propriedades mecânicas conhecidas (Módulo de Young e Coeficiente de Poisson) tanto da fundação como do solo, via dados de Sondagens, calcula-se o fator de rigidez relativa entre fundação/solo (kr). Em seguida, em função da posição excêntrica do pilar sobre a fundação, de modo a se enquadrar em um dos quatro casos possíveis indicados na Figura 7.5, se obtém os coeficientes ponderados de mola e realiza a operação conforme esquematizado na Figura 7.4b.


Exemplo 7.1: Sapata semi-flexível – Pilar Centrado

Seja a sapata e o solo com as seguintes propriedades:

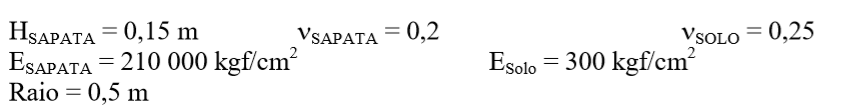
1a4efc2709e551411780660e721e2555.png

Gerando o fator de rigidez Kr = 3

Define-se os seguintes pontos sobre a sapata, Figura 7.5.

Para o caso do pilar no centro da sapata, os valores de deslocamento vertical e dos coeficientes de mola vertical são calculados e descritos a seguir.

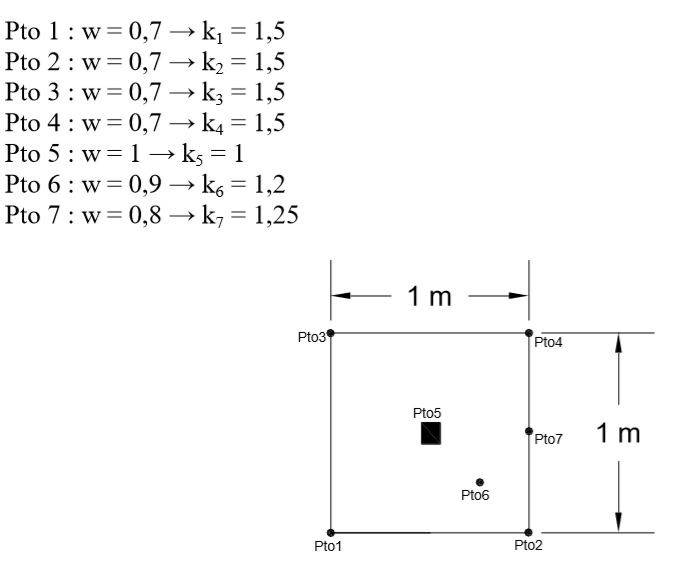
fb06bdf79feeb56e4d4b2d66b641e364.png

Figura 7.5 – Indicação dos pontos da sapata e com pilar central


Exemplo 7.2: Sapata flexível– Pilar Centrado

Seja a sapata e o solo com as seguintes propriedades:


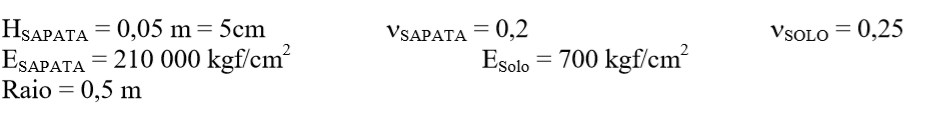
393ce847f83d11c80f706b1af2dff479.png

Gerando o fator de rigidez Kr = 0,05

Os pontos sobre a sapata é o indicado pela Figura 7.5.

Para o caso do pilar no centro da sapata, os valores de deslocamento vertical e dos coeficientes de mola vertical são calculados e descritos a seguir.

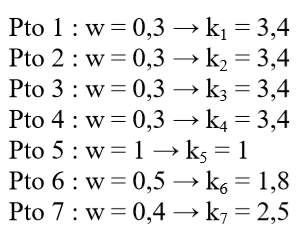
a109278f2e07a9972324bd437e180abd.png


Exemplo 7.3: Sapata semi-flexível– Pilar Pto 6

Seja a sapata e o solo com as seguintes propriedades:


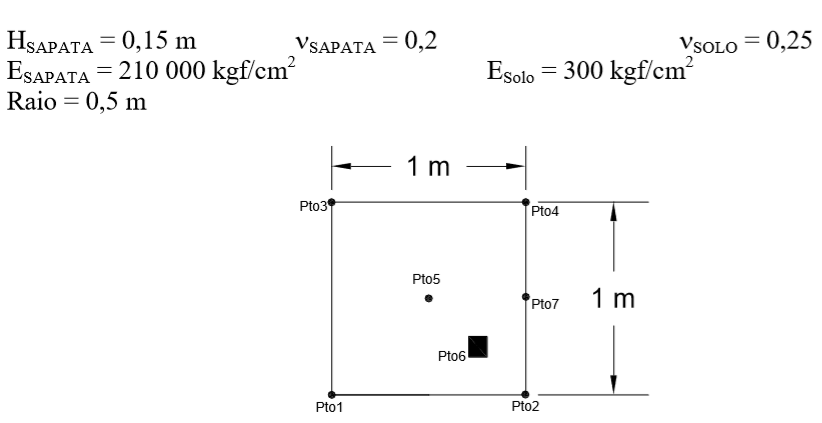
1a4086c06c1d82ab09656627298f404f.png

Figura 7.6 – Indicação dos pontos da sapata e com pilar central


Gerando o fator de rigidez Kr = 3

Para o caso do pilar no ponto 6, os valores de deslocamento vertical e dos coeficientes de mola vertical são calculados e descritos a seguir.


Pto 1 : w = 1 → k1 = 1

Pto 2 : w = 0,6 → k2 = 1,6

Pto 3 : w = 0,1 → k3 = 8,2

Pto 4 : w = 1 → k4 = 1

Pto 5 : w = 0,5 → k5 = 1,9

Pto 6 : w = 0,6 → k6 = 1,5

Pto 7 : w = 0,7 → k7 = 1,4


Exemplo 7.4: Sapata flexível – Pilar Pto 6

Seja a sapata e o solo com as seguintes propriedades:


HSAPATA = 5cm SAPATA = 0,2 SOLO = 0,25

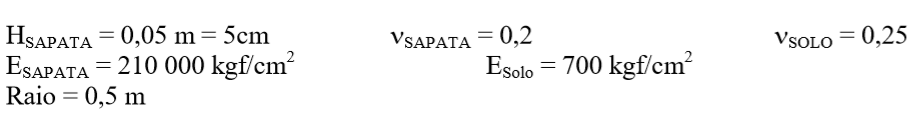
fa08c2b917137d5c13494c1e9db1d992.png


Gerando o fator de rigidez Kr = 0,05

Para o caso do pilar no ponto 6, os valores de deslocamento vertical e dos coeficientes de mola vertical são calculados e descritos a seguir.


Pto 1 : w = 0,4 → k1 = 2,8

Pto 2 : w = 0,5 → k2 = 2,1

Pto 3 : w = 0,1 → k3 = 9,9

Pto 4 : w = 0,4 → k4 = 2,8

Pto 5 : w = 0,5 → k5 = 2

Pto 6 : w = 0,9 → k6 = 1,1

Pto 7 : w = 0,6 → k7 = 1,8


Exemplo 7.5: TQS: Projeto Sap_areia

Seja o projeto Sap_areia, indicado na Figura 7.7.

O modelo gerou o fator de rigidez Kr = 76

A distribuição do coeficiente de mola para esse fator é indicada na Figura 7.8.


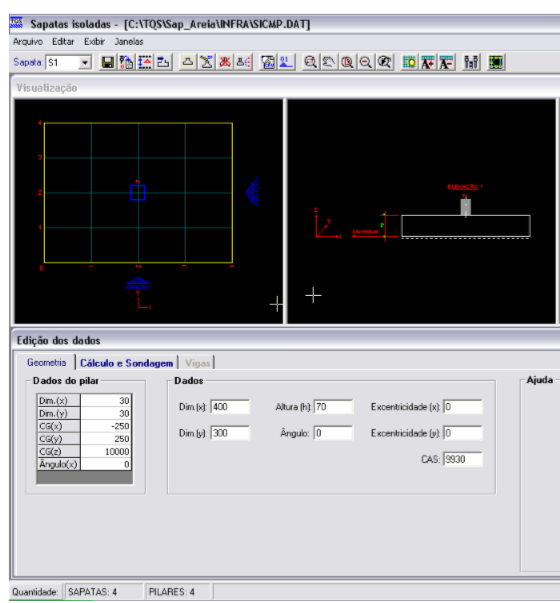
0183c9abbe9f2b8a702a002aea54510c.png


Figura 7.7 – Geometria da sapata com pilar centrado



dab49421e71078c42e85d88b7ba8b110.png

Figura 7.8 – Distribuição do Coeficiente de Mola na Sapata S1


Nas figuras 7.9 e 7.10 mostram-se outro recurso do SISES para visualização dos isovalores de tensões das fundações do projeto, respectivamente, para o caso de não se aplicar e aplicar a correção do CRV.


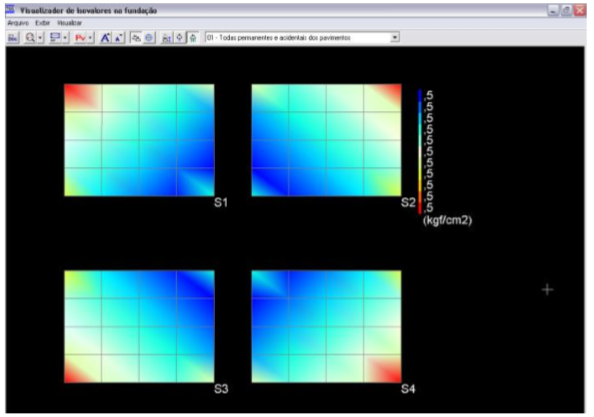
bfe886e4ac11ffcdd635de55a171a17b.png


Figura 7.9 – Isovalores de tensão para o modelo de Não-Correção do CRV


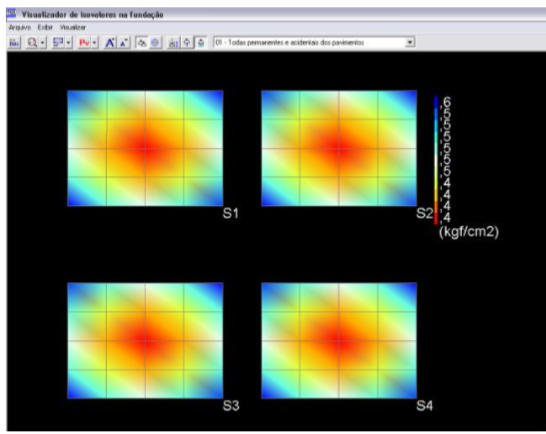
f8908fd3b637865a9cc7e80151282972.png


Figura 7.10 – Isovalores de tensão para o modelo de Correção do CRV


Para o caso de Não Correção do CRV, nos relatórios de tensões das fundações, observe nas figuras 7.11 e 7.12 que em função das tensões admissíveis definidas pelo usuário, Figura 7.11, e confrontando-as com as atuantes na fundação, Figura 7.12, não há avisos de verificação de valores ultrapassados, figura 7.11.

Por outro lado, para o caso de se aplicar a correção do CRV, nas Figuras 7.13 e 7.14, os limites são ultrapassados, veja aviso de verificação em 7.14.


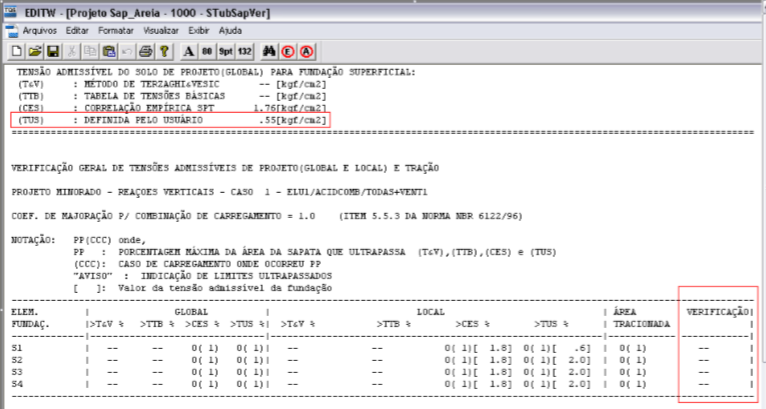
be37bd4511977232da9fee2c7957eaa4.png

Figura 7.11 – Relatório de tensões admissíveis e de verificação no modelo de Não-Correção do CRV


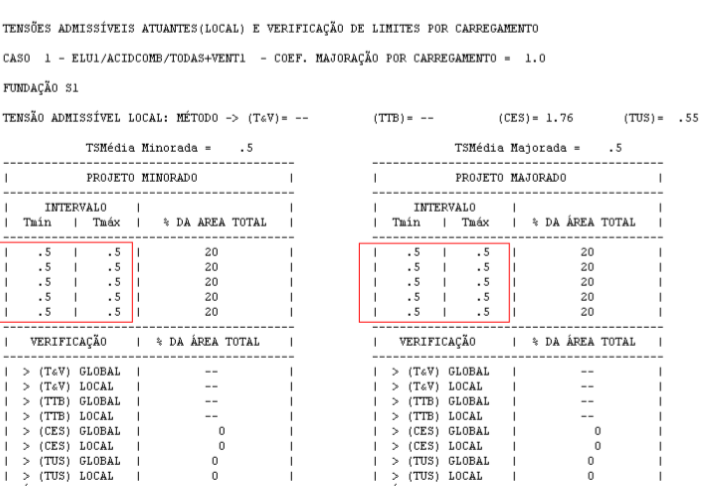
a7875074fff5dda24cb4359af82d2b25.png


Figura 7.12 – Relatório de distribuição de tensões atuantes no modelo de Não-Correção do CRV



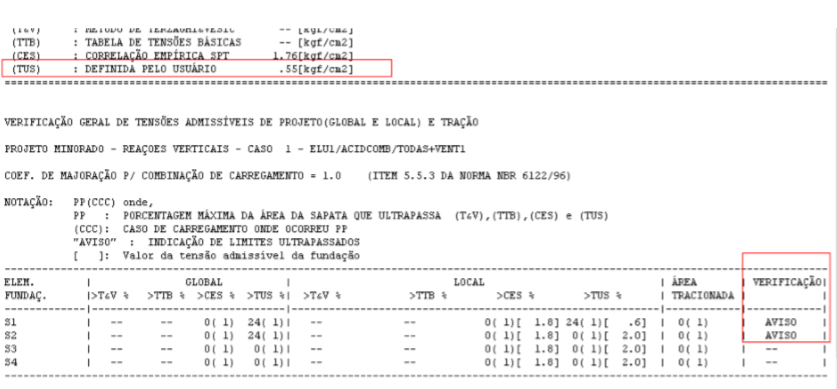
9a57bbea5f0a5655f33fcae25bd72d20.png

Figura 7.13 – Relatório de tensões admissíveis e de verificação no modelo de Correção do CRV


f0bba51fec3f70dfe736e3b47e487d76.png

Figura 7.14 – Relatório de distribuição de tensões atuantes no modelo de Correção do CRV


Modelo de Pressão de Contato

Conforme Borowicka (1936, 1938), e também indicado no livro de Teixeira & Godoy (1996), as distribuições de tensões de contato entre fundação superficial e o solo se configuram conforme gráfico apresentado na Figura 7.1, onde se tem a resposta desta para o caso de fundação de base circular de raio R e para o caso de sapata corrida.

Com o intuito de simular esta distribuição, foram aproximados curvas, via uma aproximação por mínimos quadrados com função polinomial, para os fatores de rigidezes 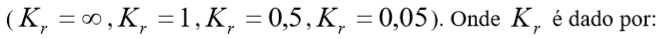6084117f75633da0108096083b9badae.png

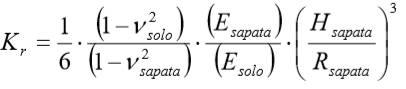
dd0d3271aae6c757d0f013a8c1290b0f.png

Com

f6e685704c7f8849778d3d8e70007b8c.png


Obs.:

Estipulou-se no Sises que se usará como referência o gráfico para a fundação circular, sendo obtido, para cada fundação retangular, um raio equivalente usando a seguinte regra:

Raio equivalente estimado em 70% do maior valor entre as dimensões da fundação, ou seja:

R = 0,7*Max[Dim(x);Dim(y)];

Emprega-se um valor fixo do Coeficiente de Poisson de 0,2, sapata = 0,2;

Foram definidos os seguintes intervalos para ponderar as pressões de contato:

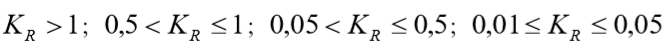
cd703354d2c37099f02f24d55470091f.png

Assim, após definir o parâmetro Kr da fundação, calcula-se - para cada ponto (X,Y) - seu fator de ponderação da pressão de contato, com o uso das curvas ajustadas conforme a Figura 7.1. Este valor calculado é usado para multiplicar o valor que fora obtido no Sises para cada ponto da fundação. Veja exemplos a seguir.


Exemplo 7.5: Fundação quadrada

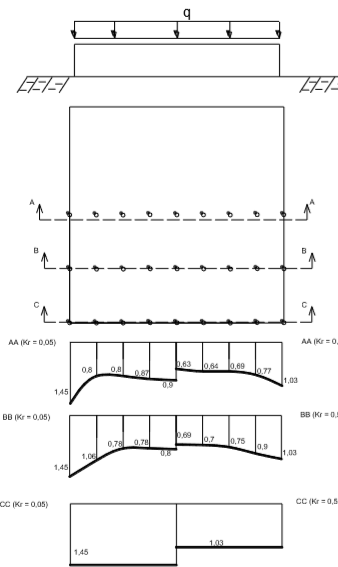
76b4bede2303416f231447b0f26a6767.png

Figura 7.15 – Fatores de ponderação da pressão de contato para Kr = 0,5 e Kr = 0,05 em diversos pontos da fundação flexível.


Obs. No Sises, na escolha do presente modelo, os valores da figura 7.15 devem ser multiplicados pela tensão obtida com o modelo sem correção para cada ponto da fundação, gerando a distribuição não-uniforme.


Dessa forma, é possível escolher no Arquivo de Critérios, veja na Figura 7.16, os seguintes procedimentos para escolha da distribuição de tensão de contato.


Modelo de Tensões de Contato com Distribuição Uniforme:

Nesse caso, como os CRVs são formulados para serem iguais para um mesmo elemento de fundação, portanto, para as combinações onde as ações verticais são predominantes as tensões de contato, em geral, também uniformes, veja Figura 7.17.

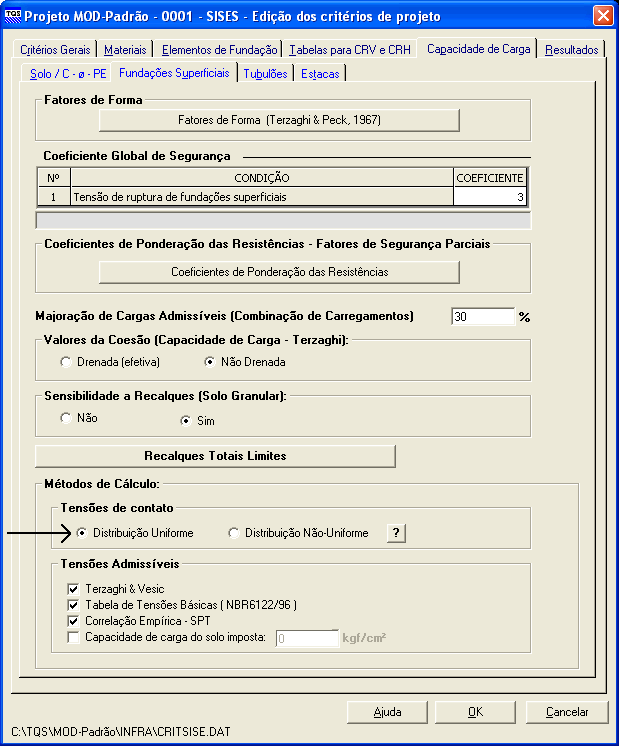
856fb7c1cf83453d15ddbd2cff96f814.png


Figura 7.16 – Escolha do Modelo Uniforme de Tensões de Contato em arquivos de Critérios



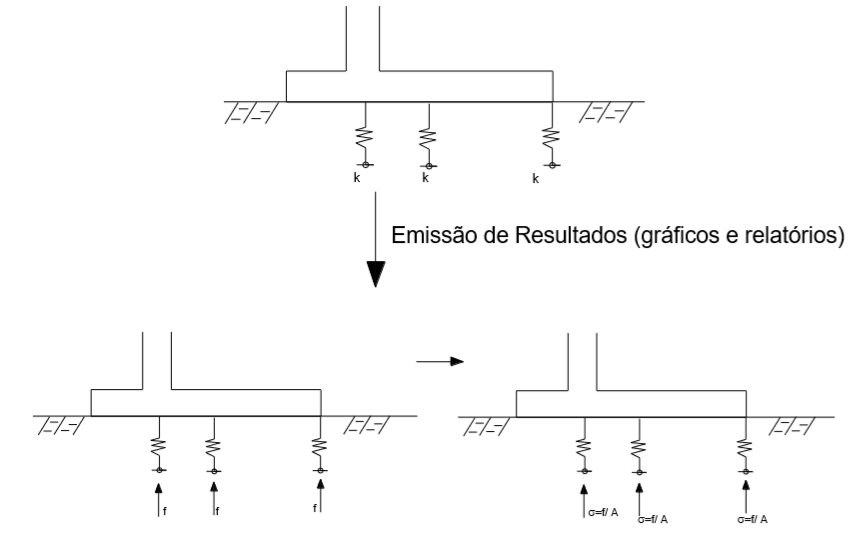
629a7f1c5732bc1ce8c5a16f2ab90b06.png

Figura 7.17 – Modelo Uniforme de Tensões de Contato


Modelo de Tensões de Contato com Distribuição Não-Uniforme:

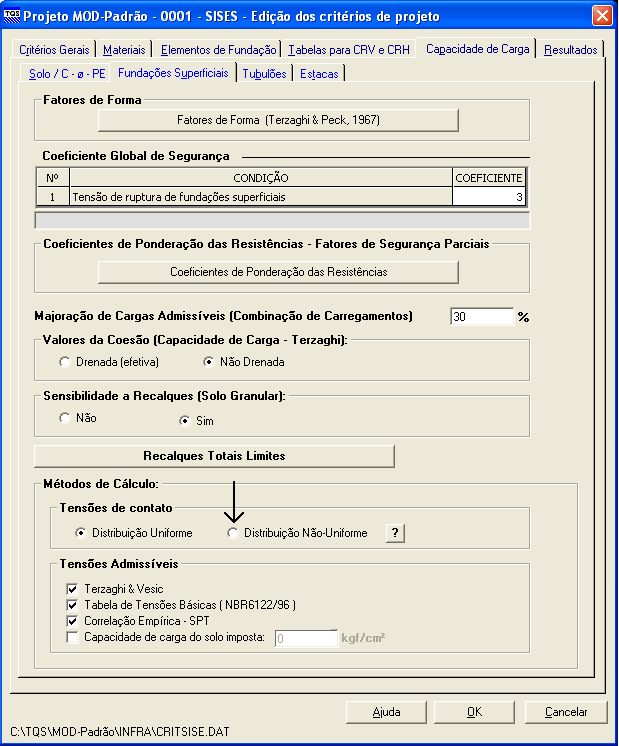
405af75557c274aa88ef46ce21f2dfef.png


Figura 7.18 – Escolha do Modelo Não-Uniforme de Tensões de Contato em arquivos de Critérios


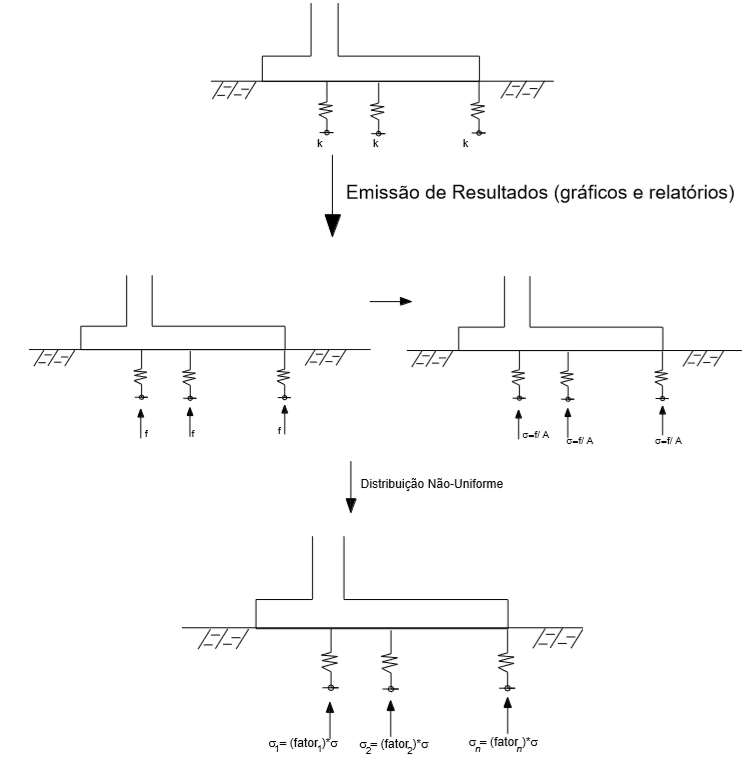
3842b2c7eb08d47f5182acd2baec88d2.png

Figura 7.19 – Modelo Não-Uniforme de Tensões de Contato


Exemplo 7.6: Projeto SapUnica_02

Nesse exemplo, com geometria indicada na Figura 7.20, mostra-se os resultados dos relatórios do Sises em forma de texto e gráficos para as duas situações: Tensão Uniforme e ao Uniforme.

As figuras 7.21 e 7.22 indicam os valores obtidos para o Modelo de Tnsão de Contato Uniforme e as Figuras 7.23 e 7.24 para as Não-Uniformes.


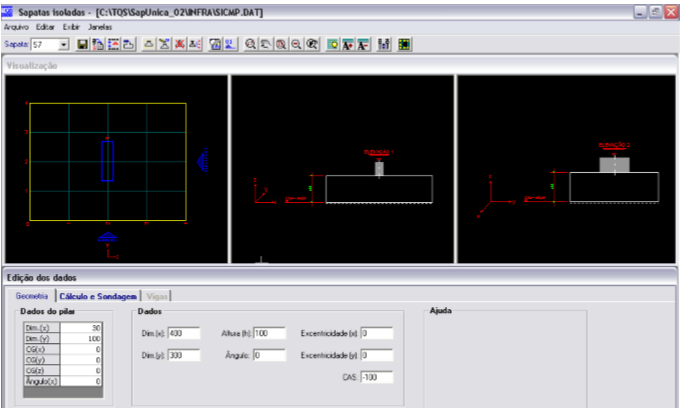
d772560002b0fe7052aede125720f946.png


cf55d5ce89b952fc0e808ef28d9d4317.png


Figura 7.20 – Geometria da sapata do projeto


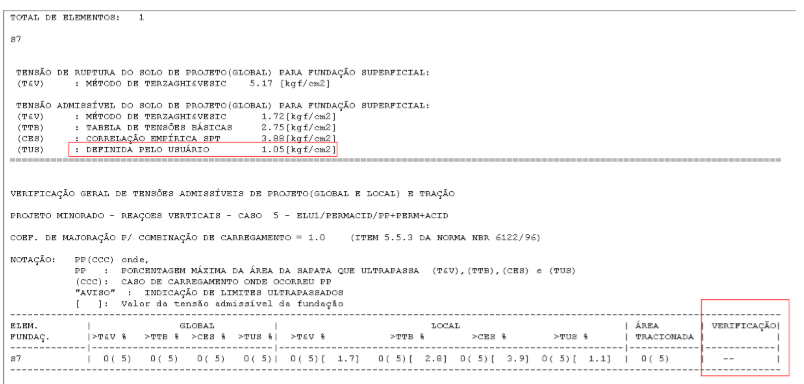
5fe19d42f34eb90186e19be9959d3a9e.png


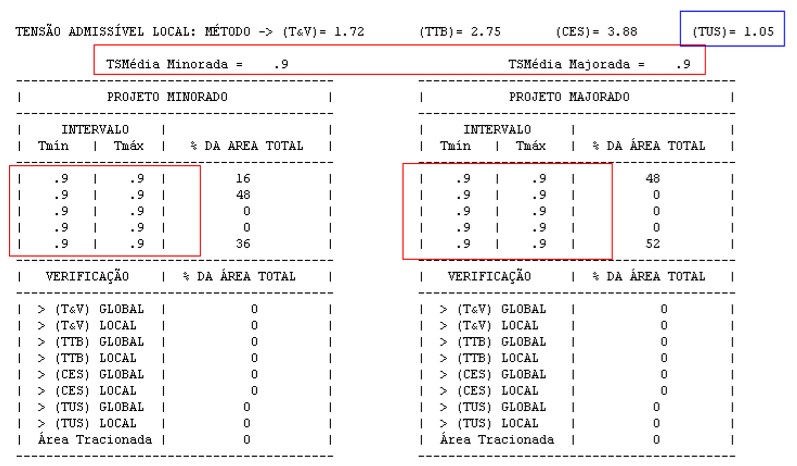
dc9cafac68e060fe089aa2d7e525b926.png


Figura 7.21 – Relatórios de distribuição uniforme das tensões atuantes e admissíveis no Sises

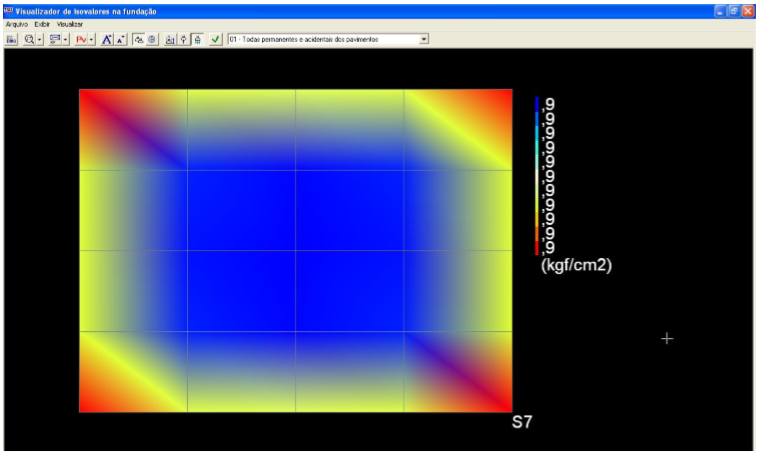
1cabbac3a494d6b2e38593983e105180.png

Figura 7.22 – Isovalores de tensão para o modelo de tensões de contato uniforme


127c3dec2287f07672d376370be0c861.png



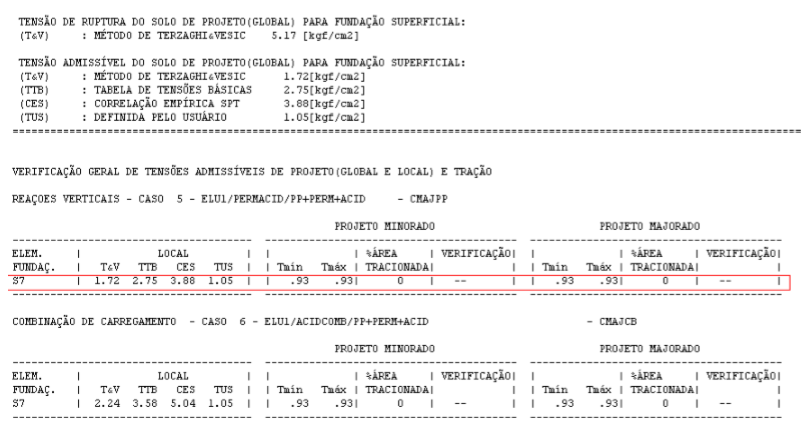
6accec8f3daec4ee7d635a2849dab76e.png


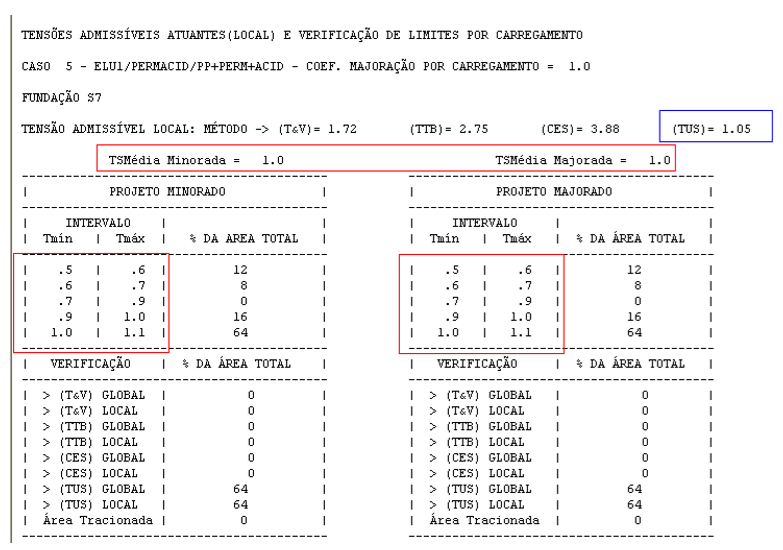
00ddd43ac0be1e0518ed2d41326ad4bc.png

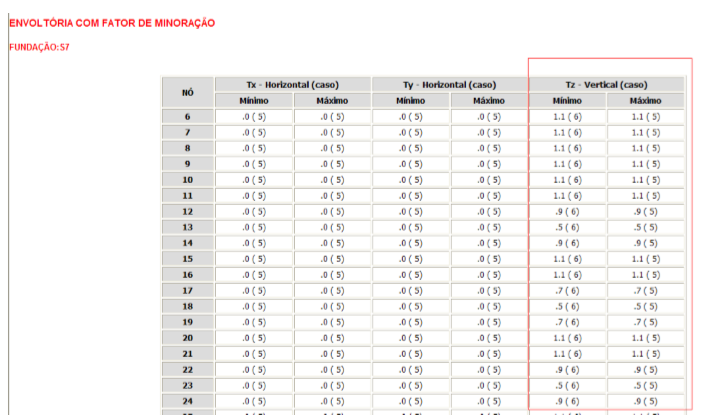
26254234e613dc1c3c25774484688b52.png


Figura 7.23 – Relatórios de distribuição não-uniforme das tensões atuantes e admissíveis no Sises



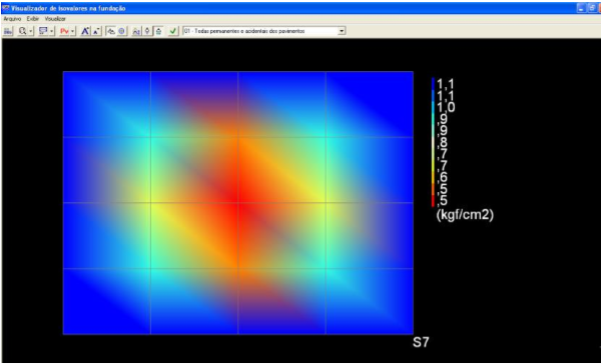
9aab49c16dd54ae7961afb28cfca8645.png

Figura 7.24 – Isovalores de tensão para o modelo de tensões de contato não-uniforme


CRH – Sapatas e Tubulões
Observações – Sapatas e Tubulões