Efeitos locais de 2ª ordem
NBR-6118:2003
O TQS PILAR trata os efeitos de 2ª ordem local de um pilar em função do seu índice de esbeltez (), conforme preconizado pela NBR-6118:2003:
a) 1
Neste caso nenhum efeito de 2ª ordem local é considerado.
O valor de 1 é calculado, para cada caso de carregamento, conforme o item 15.8.2 da NBR-6118:2003:
Sendo que 35 1 90
b) 1 < 90
Neste caso os efeitos de 2ª ordem local do pilar devem ser considerados. São utilizados os métodos aproximados conforme os itens 15.8.3.3.2 e 15.8.3.3.3 da NBR-6118:2003:
Método do pilar-padrão com curvatura aproximada
Método do pilar-padrão com kapa aproximado
c) 90 < 140
Neste caso os efeitos de 2ª ordem local do pilar devem ser considerados. Nesta situação o método utilizado é, conforme o item 15.8.3.3.4 da NBR-6118:2003, o do pilar-padrão acoplado a diagramas M,N,1/r.
d) 140 < 200
Neste caso os efeitos de 2ª ordem local do pilar devem, obrigatoriamente, ser considerados utilizando o Método Geral, conforme o item 15.8.3.1 da NBR-6118:2003.
NBR-6118:1980 e NB1/60
No TQS Pilar, o efeito local de 2ª ordem é tratada diferentemente segundo as três classificações abaixo ( é o lambda, índice de esbeltez do pilar):
a) 40
Neste caso o pilar é tratado como curto e nenhum efeito de local de 2ª ordem é considerado.
b) 40 < 80
Neste caso o pilar é considerado como médio e o efeito de 2ª ordem deve ser considerado. O tratamento teórico é o processo simplificado apresentado na NBR 6118, item 4.1.1.3.C.
c) > 80
Neste caso o pilar é considerado como esbelto e os efeitos de 2ª ordem devem ser considerados obrigatoriamente. No TQS Pilar, oferecemos um programa específico, que realiza o estudo destes pilares, através de verificações iterativas. Os efeitos da 2ª ordem, tanto a não linearidade geométrica como a física são analisados.
Estes pilares geralmente são anti-econômicos e devem ser evitadas pelo excesso de armadura resultante do dimensionamento.
Considerações gerais sobre efeitos locais de 2ª ordem
Na antiga NB-1/60, o limite máximo do para a não consideração dos efeitos de 2ª ordem de forma rigorosa era o valor 100.
Na NBR6118:1980 essa exigência passou para > 80.
Na norma NBR6118:2003 a exigência para processos mais rigorosos passaram a ser 90 (pilar-padrão acoplado a diagramas M,N,1/r) e 140 (Método Geral), sempre inferiores a 200.
Por esta razão, o arquivo de critérios do TQS Pilar permite a alteração dos limites para a consideração da 2ª ordem e dos métodos a serem utilizados. Cabe a cada usuário a adoção dos critérios mais convenientes.
Não cabe ao TQS Pilar o mérito do acerto ou não destes critérios. Cabe a cada usuário a adoção do limite do que for mais adequado ao seu processo de projeto.
Código modelo MC-78 do CEB/FIP também considera valores diferentes das adotadas pela NB-1/78.
Efeitos locais de 2ª ordem – NBR 6118:2003
A NBR 6118:2003 permite o uso de 4 métodos para análise local de 2ª ordem. São eles:
Pilar-Padrão com 1/r aproximada
Pilar-padrão com rigidez kapa aproximada
Pilar-padrão acoplado a diagrama N, M, 1/r
Método Geral
Os três primeiros métodos são considerados processos aproximados e são descritos no item 15.8.3.3 da NBR 6118:2003, enquanto que o Método geral (item 15.8.3.2 da NBR 6118:2003), como a própria nomenclatura já deixa meio evidente, é um processo mais abrangente e sofisticado.
Vale lembrar que na extinta NBR 6118:1980 havia apenas um método disponível, o pilar-padrão com curvatura aproximada, cuja formulação era praticamente similar à atual.
Cada um desses métodos possui limitações próprias, e por isso, podem ser aplicados desde que a esbeltez do pilar esteja dentro de um certo patamar. Evidentemente, os processos aproximados possuem uma limitação maior.
- Esbeltez limite
Os métodos do pilar-padrão com 1/r aproximada e pilar-padrão com aproximada podem ser utilizados em pilares com esbeltez máxima igual a 90, segundo a NBR-6118:2003. O método do pilar-padrão acoplado a diagrama N, M, 1/r é limitado para uma esbeltez máxima de 140. O método geral, por sua vez, pode ser usado até um limite de 200.
Acima desse valor, a norma não permite o uso de nenhum método, a não ser em casos de postes onde a força normal de compressão é baixa.
O TQS Pilar não faz o processamento de pilares com esbeltez maior que 200.
Métodos aproximados
Antes mesmo de iniciar o estudo da formulação de cada um dos métodos aproximados, pela própria nomenclatura dos mesmos é possível tirar algumas conclusões prévias. Note que os três processos aproximados fazem o uso de um termo comum: “pilar-padrão”.
- O que é pilar-padrão?
Conforme já sabemos, o cálculo da deformada do lance de um pilar à medida que o carregamento é aplicado sobre o mesmo, é um dos desafios presentes na análise local em 2ª ordem. Como tratar a não-linearidade geométrica num lance de pilar?
O método do pilar-padrão consiste numa aproximação que pressupõe que a deformada final do pilar será representada por uma curva senoidal. Existem inúmeros estudos que comprovam a eficiência dessa simplificação, válida até um determinado limite de esbeltez.
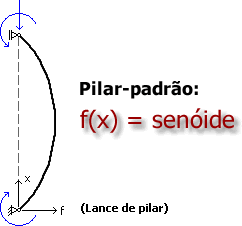
Uma vez definida a forma final do lance do pilar (senóide), é possível então chegar a uma solução analítica para o problema da não-linearidade geométrica, obtendo-se expressões relativamente simples que podem ser utilizadas no cálculo do pilar.
Dessa forma, conclui-se que os três processos aproximados presentes na NBR 6118:2003, tratam a não-linearidade geométrica (NLG) de forma idêntica.
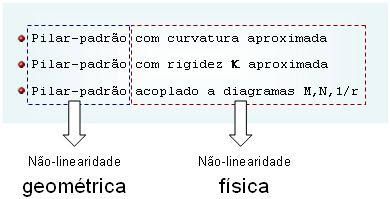
O que diferencia um método aproximado do outro é justamente as diferentes maneiras de considerar a outra não-linearidade, a física (NLF).
Pilar-padrão com 1/r aproximada
- Aplicabilidade
Esse método pode ser empregado apenas para pilares com ≤ 90, seção constante e armadura simétrica e constante ao longo de seu eixo.
Não-linearidade geométrica
Admite-se que a deformação da barra seja senoidal (pilar-padrão).
- Não-linearidade física
A rigidez do lance do pilar é obtida por meio da definição de uma curvatura aproximada na seção crítica.
- Formulação
A formulação é extremamente simples e possibilita o cálculo manual. O momento total (1ª ordem + 2ª ordem) máximo no pilar é calculado pela seguinte expressão:
, sendo
Onde:
e
O momento de 2ª corresponde à parcela Nd.(le2/10).(1/r).
Note que não é necessário conhecer previamente a armadura do pilar para aplicar as fórmulas acima.
Pilar-padrão com rigidez kapa aproximada
- Aplicabilidade
O método do pilar-padrão com rigidez kapa aproximada pode ser adotado na análise de pilares retangulares com ≤ 90, com armadura simétrica e constante ao longo de seu eixo.
- Não-linearidade geométrica
Admite-se que a deformação da barra seja senoidal (pilar-padrão).
- Não-linearidade física1
A não-linearidade física no lance do pilar é considerada por meio de uma expressão aproximada para rigidez, cuja dedução foi obtida durante a tese de doutoramento do prof. .
O valor da rigidez é tomado de forma adimensional e é denominado de rigidez (“kapa”).
- Formulação
Assim como o método do pilar-padrão com 1/r aproximada, a formulação do pilar-padrão com kapa aproximada é simples e possibilita o cálculo manual.
Segundo a formulação apresentada na NBR 6118:2003, o cálculo do momento total máximo MSd,tot deve ser realizado de forma iterativa em função da rigidez adimensional, de acordo com as seguintes fórmulas:
O momento de 2ª ordem é calculado por uma amplificação da 1ª (b.MS1d,A).
Note que não é necessário conhecer previamente a armadura do pilar para aplicar as fórmulas acima.
Pilar-padrão acoplado a diagramas N, M, 1/r
- Aplicabilidade
Esse método pode ser empregado apenas para pilares com ≤ 140.
- Não-linearidade geométrica
Admite-se que a deformação da barra seja senoidal (pilar-padrão).
- Não-linearidade física
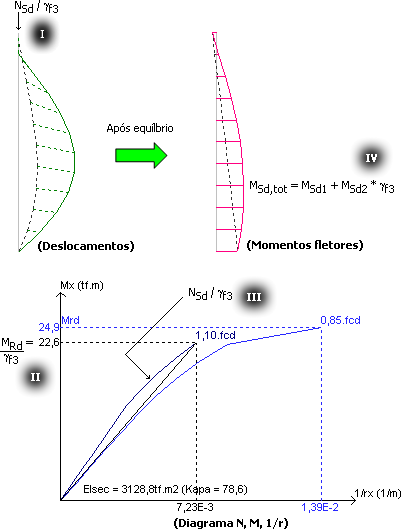
A não-linearidade física é considerada por meio da obtenção da rigidez no diagrama N, M, 1/r proposto pela NBR 6118:2003, conforme mostra a figura a seguir.
Note que há uma relação entre a rigidez secante EIsec e a rigidez adimensional kapa.
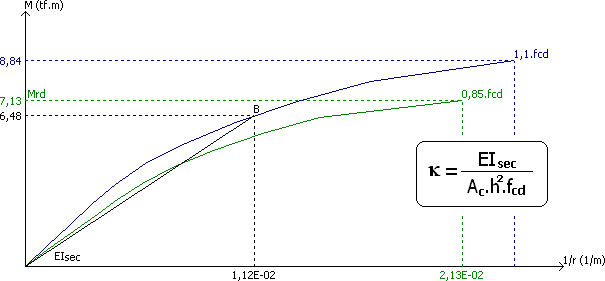
Muito embora tenha o mesmo nome da rigidez adimensional calculada no método do pilar-padrão com rigidez aproximada, essa rigidez kapa obtida pelo diagrama (rigidez acoplada ao diagrama N, M, 1/r) é mais precisa.
Poderíamos dizer que se trata de uma rigidez “mais refinada e real”.
- Formulação
O momento total máximo MSd,tot é calculado exatamente pela mesma fórmula do método do pilar-padrão com rigidez aproximada:
No entanto, deve-se ficar bem claro que o valor da rigidez kapa a ser utilizado na fórmula é o obtido pelo diagrama normal-momento-curvatura, e não a rigidez kapa aproximada.
Quando se faz o uso do coeficiente f3, a fórmula para obtenção do momento total fica assim:
Duas observações muito importantes com relação ao método do pilar-padrão acoplado ao diagrama N, M, 1/r:
Trata-se de um método que, na prática, somente é viável com o uso de um computador, pois como vimos no início deste curso, a montagem do diagrama N, M, 1/r é extremamente complicada de ser realizada manualmente.
É necessário que a armadura existente no lance do pilar seja previamente conhecida, pois não há diagrama N, M, 1/r sem armadura definida! Ou seja, o processo de dimensionamento é realizado por um processo iterativo de verificações.
Resumo
A tabela a seguir apresenta um resumo das principais características de cada um dos métodos aproximados.
| Pilar-padrão com 1/r aproximada | Pilar-padrão com rigidez aproximada | Pilar-padrão acoplado a diagrama N, M, 1/r | |
| Item da NBR 6118 | 15.8.3.3.2 | 15.8.3.3.3 | 15.8.3.3.4 |
| NLG | Pilar-padrão | Pilar-padrão | Pilar-padrão |
| NLF | |||
| Esbeltez limite | ≤ 90 | ≤ 90 | ≤ 140 |
| Cálculo manual | Sim | Sim | Não |
| Necessita As conhecido | Não | Não | Sim |
Método geral
No item anterior, foram apresentados três métodos aproximados para análise dos efeitos locais de 2ª ordem. Agora, vamos estudar um processo mais abrangente e sofisticado, usualmente chamado de Método Geral (item 15.8.3.2 da NBR 6118:2003).
- NBR 6118:2003
O método geral é definido na NBR 6118:2003, item 15.8.3.2, por apenas uma única frase:
“Consiste na análise não-linear de 2a. ordem efetuada com discretização adequada da barra, consideração da relação momento-curvatura real em cada seção, e consideração da não-linearidade geométrica de maneira não aproximada.”
Nesse item, não existe nenhuma formulação definida, e muito menos uma descrição detalhada de como aplicar o método. Somente existe a definição acima, e nada mais.
Dessa frase, podemos extrair as seguintes informações principais:
Discretização adequada
Relação Momento-Curvatura
NLG não aproximada
- Aplicabilidade
O método geral pode ser empregado apenas para pilares com ≤ 200 e é obrigatório para pilares com > 140. Acima desse último limite (140), não se pode aplicar nenhum dos processos aproximados estudados anteriormente.
- Não-linearidade geométrica
As deformações ao longo lance do pilar devem ser analisadas por processo refinado. Não se pode adotar a aproximação por uma curva senoidal (pilar-padrão).

Existem diferentes maneiras para considerar a não-linearidade geométrica de forma refinada. Uma primeira alternativa é a partir do diagrama de momentos fletores no lance do pilar, obter as curvaturas (1/r) por meio da rigidez EI, as rotações e deslocamentos (d) por meio de integrações sucessivas, e depois, com esses incrementar os momentos de 2ª ordem nos esforços originais. Esse cálculo é repetido inúmeras vezes até o acréscimo de esforços ou deslocamentos tender a zero.
Uma outra forma de tratar o problema é utilizar modelos numéricos que possibilitem a análise em 2ª ordem (equilíbrio na posição deformada), como por exemplo, o cálculo de um pórtico espacial por meio de uma análise P-Delta.
Seja qual for o processo empregado, a informação principal que se busca é a posição final de equilíbrio do lance do pilar, de tal forma a definir a magnitude total dos efeitos locais de 2ª ordem.

A busca dessa posição de equilíbrio é sempre iterativa. E, por isso, é fundamental que sejam consideradas tolerâncias que controlem a convergência dos processos de forma eficiente e segura. Usualmente, esses valores são definidos em “deltas máximos de deslocamentos ou esforços”.
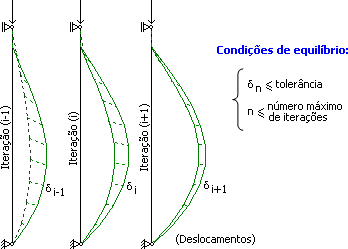
- Instabilidade local
Ao empregar um processo aproximado (pilar-padrão com 1/r aproximada, pilar-padrão com kapa aproximada, pilar-padrão acoplado a diagrama N, M, 1/r), a única resposta final que temos é se o lance de pilar passa ou não em relação à resistência última da seção crítica (ruptura).
Já, no método geral, além dessa informação (ruptura da seção crítica), pode-se flagrar se o lance é estável ou instável, pois a busca pela posição de equilíbrio do mesmo é itertiva.

Ao adotar o método geral no cálculo de um pilar demasiadamente esbelto, por exemplo, pode-se se chegar numa situação de instabilidade quando o número máximo de iterações definido na análise é alcançado.
Nesse caso, o processo não converge pois os acréscimos de deslocamentos a cada iteração são superiores à tolerância adotada. Esse resultado independe do nível de solicitação da seção crítica em relação à sua resistência.
- Não-linearidade física
A não-linearidade física é considerada por meio da obtenção da rigidez no diagrama N, M, 1/r. Essa rigidez pode ser definida das seguintes formas:
Pela rigidez secante EIsec obtida pela linearização do diagrama (reta), e que pode ser estendida para todas as seções do lance. É a forma mais recomendável de se obter a rigidez, pois está a favor de segurança bem como facilita a análise (desacoplamento das duas direções).
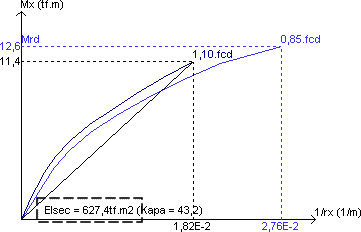
Pela rigidez secante EI obtida pela curva para cada seção do lance de acordo com a sua solicitação atuante. Trata-se de um procedimento válido somente para casos de flexão composta normal.
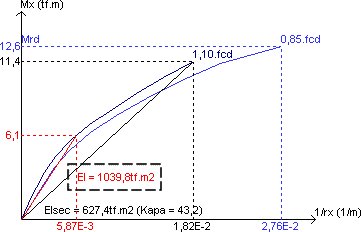
Pela rigidez secante oblíqua em que considerem simultaneamente os esforços solicitantes em ambas as direções dos pilares.
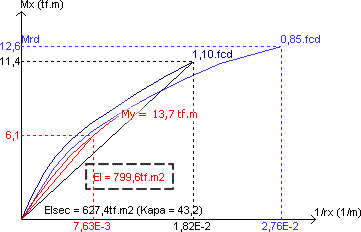
- Discretização adequada
No método geral, é fundamental que o lance do pilar seja discretizado adequadamente, de tal forma a obter as respostas em várias seções.
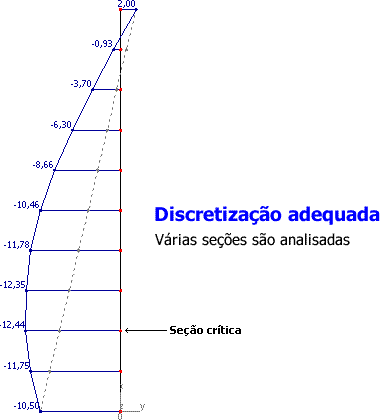
Ao contrário dos processos aproximados em que a definição da seção crítica entre o topo e a base do lance do pilar era realizada de forma simplificada pelo coeficiente b, no método geral essa seção é definida de forma bem mais realista.
Em lances de pilares de edifícios usuais, a discretização em 10 trechos é suficiente.
- Coeficiente f3
Pode ser considerada a formulação de segurança em que se calculam os efeitos de 2ª ordem das cargas majoradas de f/f3, que posteriormente são majorados de f3.
Processo de verificação
O método geral é essencialmente um processo de verificação, pois é necessário conhecer previamente a armadura ao longo do lance do pilar para calcular os esforços de 2ª ordem.
Dessa forma, assim como no método do pilar-padrão acoplado a diagrama N, M, 1/r, o processo de dimensionamento pelo método geral é iterativo. Define-se uma armadura e analisa-se o pilar sucessivamente, até a obtenção de uma armadura necessária.
Cálculo manual
Calcular manualmente um lance de pilar pelo método geral é inviável, visto que é necessário considerar tanto a não-linearidade física como a geométrica de forma refinada. Na prática, o emprego do método geral somente é realizado com o uso de um computador.
Cabe ao Engenheiro de Estruturas conhecer a teoria que envolve o método, de tal forma a poder interpretar os resultados obtidos de forma segura.
Resumo geral
Até o momento, estudamos com detalhes todos os processos presentes na NBR 6118:2003. Através de exemplos, foi possível perceber as particularidades e simplificações inerentes de cada método.
O gráfico a seguir traz um resumo com relação à aplicabilidade de cada um dos métodos.

A determinação do e esforços no ponto médio
Este item é aplicável para projetos processados pela NBR6118:1980.
a) Determinação do em função do carregamento
Em muitos casos, as solicitações atuantes nos diversos pilares são compostas por uma força normal e dois momentos fletores. Principalmente quando estas solicitações são devidas ao modelo de pórtico espacial, a linha neutra resultante do dimensionamento da seção transversal, geralmente, não é paralela ao um dos eixos principais de inércia. Por esta razão foi criado um critério no TQS Pilar, critério K6, 'Consideração dos momentos de 2ª ordem', que permite o cálculo do em função desta linha neutra com uma aproximação, que é considerar a linha neutra paralela ao plano de atuação dos momentos fletores. Com isto, muitos pilares aparentemente esbeltos, passam a ter o índice de esbeltez menor, pois o nesta direção é menor que o calculado na direção da maior esbeltez, podendo serem considerados como pilares curtos. Este é um critério que reduz as armaduras nos pilares e deve ser criteriosamente selecionado pelo usuário.
b)Esforços de 2ª ordem no ponto médio do lance.
O TQS Pilar realiza, para os pilares esbeltos, o dimensionamento da seção transversal do pilar para os valores das solicitações no topo e na base do lance. Para o ponto médio do lance, onde se estudam os efeitos da 2ª ordem, principalmente quando os esforços são provenientes de cálculo do modelo de pórtico espacial, encontra-se uma dificuldade pois o plano de atuação do momento resultante no topo do pilar não coincide com o plano de atuação do momento resultante na base do pilar. Neste caso, dois critérios estão disponíveis para a escolha do usuário:
b1) No topo e na base do pilar, os momentos são projetados segundo os eixos principais de inércia, x e y, e os momentos de 2ª ordem são determinado no ponto médio do pilar para estas direções x e y. Posteriormente, é calculado o momento no ponto médio como resultante entre estes dois momentos determinados. A figura abaixo ilustra estes valores de momentos.
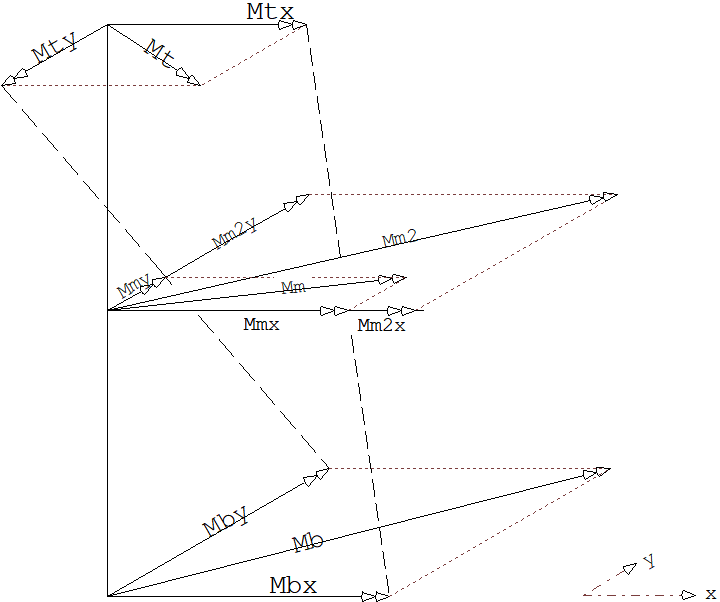
Onde:
Mt é a resultante do momento no topo
Mb é a resultante do momento na base
Mtx e Mty são projeções de Mt nos eixos x e y
Mbx e Mby são projeções de Mb nos eixos x e y
Mmy é o valor do momento no ponto médio, direção y
Mmx é o valor do momento no ponto médio, direção x
Mm2x é o valor de Mmx com efeito de 2a. ordem, direção x
Mm2y é o valor de Mmy com efeito de 2a. ordem, direção y
Mm2 é a resultante dos momentos Mm2x e Mm2y
b2) No topo e na base do pilar, os momentos não são projetados nos eixos principais de inércia e a análise é feita tomando-se como plano válido, o plano que contém o maior momento. O momento menor na outra extremidade é projetado neste plano inicial adotado. Temos 2 casos a considerar. Se a diferença angular entre estes dois planos projetados num plano vertical for 15º, os dois momentos são considerados coplanares.
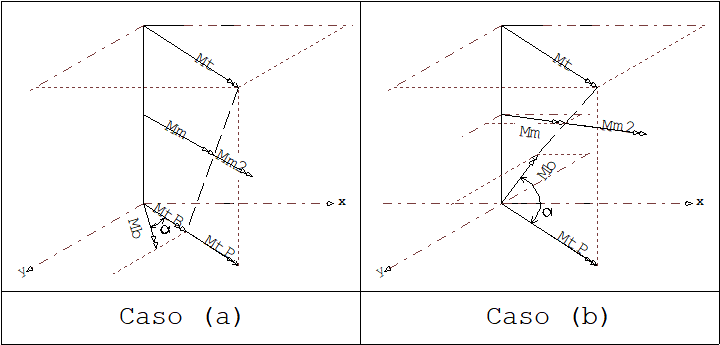
Onde:
Mt é a resultante do momento no topo, e é maior, em módulo, que Mb
Mb é a resultante do momento na base
MtP é o momento Mt projetado na base
MbP é o momento Mb projetado no plano de Mt e MtP
Mm é o valor do momento no ponto médio do plano Mt e MbP
Mm2 é o valor de Mm com efeito de 2a. ordem
é o ângulo formado entre os dois planos verticais que contém os momentos Mt e Mb.
No caso (a), se o ângulo for 15º, o momento Mb será considerado como atuando no mesmo plano do momento Mt, isto é, serão coplanares os momentos.
Caso o ângulo for > 15º, o momento Mb será considerado como não atuando no plano vertical que contém o momento Mb.
Índice de esbeltez > 80
A aplicação deste item é aplicável para projetos processados pela NBR6118:1980.
Neste caso, a verificação do esgotamento da capacidade da seção transversal do pilar por ruptura ou por instabilidade geral é feita através da consideração da relação momento - curvatura da seção transversal do pilar em diversos pontos do lance. É considerado neste método a não linearidade física dos materiais através dos diagramas tensão - deformação para o aço e para o concreto. A não linearidade geométrica do pilar é considerada através dos efeitos da posição deformada do eixo do pilar sob a atuação das cargas verticais e horizontais.
Este é um cálculo singular, interativo, que deve ser realizado apenas para alguns pilares especiais onde os efeitos de 2ª ordem não podem ser analisados por outros processos. O processo adotado é o de verificação da estrutura e, por esta razão, deve-se fornecer a dimensão da seção e as armaduras ao longo do pilar. O pilar pode ter, inclusive, seção transversal com variação nas suas dimensões ao longo do lance.
O cálculo é baseado no método dos deslocamentos. O pilar é discretizado em diversos segmentos conectados aos nós da estrutura.
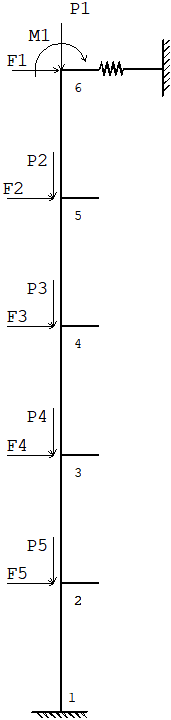
Em cada segmento as características dos materiais são consideradas constantes. Permite-se a definição de vínculos elásticos nos extremos do pilar e as cargas atuantes nas 3 direções (3 forças e 3 momentos) nos nós do modelo estrutural. A armadura do pilar deve ser fornecida através da definição da porcentagem (da armadura total) existente em cada face da seção. Apenas seções retangulares e circulares (cheias ou vazadas) estão disponíveis.
O cálculo é interativo. Os seguintes passos são adotados:
- Determinação da posição deformada do pilar sob o efeito da 1ª ordem.
- Solicitações nos diversos segmentos.
- Alteração da geometria da estrutura para a nova posição deformada.
- Nova rigidez dos segmentos em função das solicitações e dos materiais.
- Na próxima iteração o carregamento da estrutura atuará na posição deformada.
- Determinação da posição deformada do pilar sob o efeito da 2ª iteração.
- Solicitações nos diversos segmentos.
- Alteração da geometria da estrutura para a nova posição deformada.
-Nova rigidez dos segmentos em função das solicitações e dos materiais.
O processo se repete até que a posição deformada entre uma iteração e outra seja menor que uma certa tolerância e, não tenha sido atingido o esgotamento da capacidade resistente das seções transversais do pilar.
Como resultado do processamento é emitida mensagem se o pilar é estável ou não (houve convergência entre esforços externos e internos em cada seção considerando todos os efeitos de 2a. ordem), para o carregamento dado. Também são impressos os deslocamentos, reações de apoio e esforços solicitantes nos diversos segmentos (barras) do pilar nas 3 direções (3 forças e 3 valores de momentos).
Pela singularidade da análise, este processo de verificação, embora geral, está disponível para a verificação isolada de pilares e não está integrado aos dados gerais e armaduras determinadas automaticamente pelo TQS Pilar.
