Área total - k140
Cálculo da área total para estribos de 4 e 6 ramos
Objetivo: reduzir a quantidade total de armaduras de estribos quando temos vigas muito carregadas com cisalhamento e torção.
Opções:
- “Caso 1”: Considera que a parcela do estribo periférico que resiste à força cortante é igual a parcela resistida pelos ramos internos. Evidentemente que a área total de estribos na seção devido a força cortante será sempre igual a área total necessária. Neste caso, a área do estribo periférico para a força cortante é complementada com a área do estribo necessária devido a torção.
- “Caso2”: Considera que a parcela do estribo periférico que resiste à força cortante é menor que a parcela resistida pelos ramos internos. Evidentemente que a área total de estribos na seção devido a força cortante será sempre igual a área total necessária. Neste caso, a área do estribo periférico é complementada com a área do estribo necessária devido a torção.
Obs.: Este critério tem relação direta com um critério similar para o detalhamento a torção: <Otimização no detalhamento de estribos de 4 e 6 ramos> pois ambos tratam a mesma questão de redução da quantidade de armaduras detalhadas.
Caso for selecionada a opção <Otimizado>, no critério <Otimização no detalhamento de estribos de 4 e 6 ramos>, obrigatoriamente neste critério de <Cálculo de área total de estribos> será imposta a opção "Caso 1". A opção “Caso 2” é incompatível com a opção <Otimizado>.
I)Como as armaduras são calculadas no “Caso 1”
Equacionando:
AsV : área de estribos devido a força cortante total
AsT : área de estribos devido ao momento de torção para cada ramo de estribo
= Seção transversal com estribos com 4 ramos:
As1R área por ramo de estribos: AsV/4. + AsT
As4R área para os 4 ramos: As1R * 4.
= Seção transversal com estribos com 6 ramos:
As1R área por ramo de estribos: AsV/6. + AsT
As6R área para os 6 ramos: As1R * 6.
II)Como as armaduras são calculadas no “Caso 2”
Equacionando:
AsV: área de estribos devido a força cortante total.
AsT : área de estribos devido ao momento de torção para cada ramo de estribo
AsV1: área do estribo devido a força cortante, ramo externo
AsV2: área do estribo devido a força cortante, ramo interno
= Seção transversal com estribos com 4 ramos:
AsV1 = (AsV – 2.*AsT) / 4.
AsV2 = AsV1 + AsT
Área por ramo de estribo: AsV2
Área para os 4 ramos de estribos: AsV2 * 4.
= Seção transversal com estribos com 6 ramos:
AsV1 = (AsV – 4.*AsT) / 6.
AsV2 = AsV1 + AsT
Área por ramo de estribo: AsV2
Área para os 6 ramos de estribos: AsV2 * 6
III) Exemplo
AsV = 20 cm2
AsT = 5 cm2
Estribos de 4 ramos
AsV1 = 2.5 cm2
AsV2 = 7.5 cm2
Área para os 4 ramos de estribos: 7.5 * 4 = 30 cm2
Pelo processo do “Caso 1”, para os 4 ramos de estribos temos: (20/4.+5)*4 = 40 cm2
Esta hipótese é válida para o caso de se adotar, para força cortante, uma parcela de armadura menor para os estribos periféricos do que para os estribos centrais.
IV)Tipo de Estribo
Deve-se observar que este caso de redução das bitolas dos estribos inferiores somente é válido para a situação onde existe um estribo que percorre todo o contorno da seção (este é o estribo que resiste a torção). Os demais estribos ficam restritos a região interna da seção conforme figura abaixo.
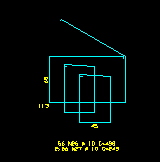 | 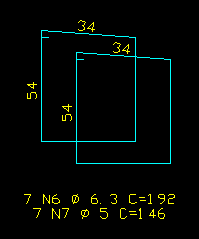 |
| Detalhamento correto | Detalhamento incorreto |
