Punção
Introdução
A verificação e dimensionamento a punção utiliza a formulação proposta pela ABNT NBR 6118 como base de cálculo, fazendo algumas considerações para tratamento de situações não abordadas pela norma.
Histórico
Anteriormente, a verificações tomava os valores obtidos das barras do modelo de grelha para o cálculo das ações em cada perímetro de punção. Apesar de ter uma proposta mais refinada, esta abordagem dependia grandemente da discretização do modelo e poderia facilmente apresentar valores não previstos pela abordagem da norma.
Desta forma, a partir da V23, optou-se pela utilização direta do conceito apresentado pelo ABNT NBR 6118.
Teoria utilizada
A análise de punção é feita considerando a análise plástica. Ou seja, já está prevista a fissuração do concreto e apenas mecanismos fora a integridade do concreto são utilizados para definição da resistência máxima.
Nesta situação de análise plástica, a distribuição de tensões de cisalhamento no perímetro crítico tem o seguinte aspecto:
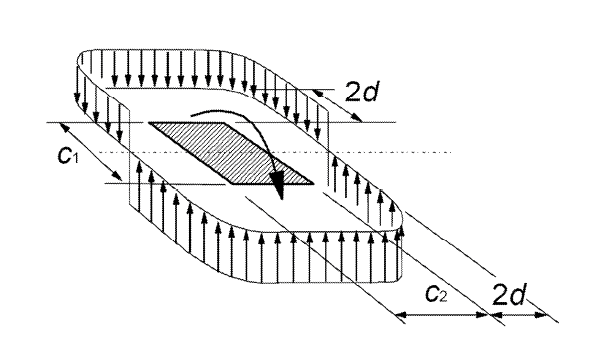
Observem que, para um momento aplicado, a tensão máxima de cisalhamento tem o mesmo módulo para todo trecho do perímetro crítico.
Apenas para ilustrar, segue o diagrama de tensõesXdeformações “clássico” para a situação elástica, elasto-plástica e plástico:
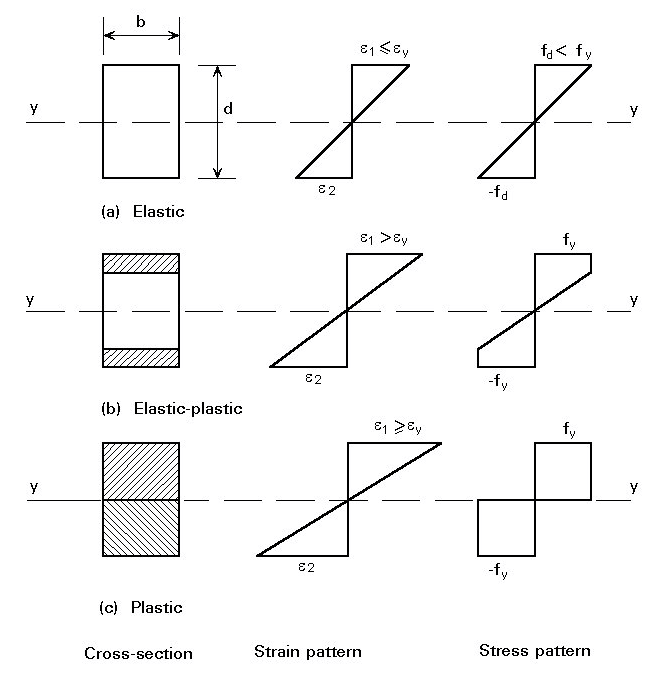
Observem que a distribuição de tensões no perímetro crítico tem o aspecto esperado (mesmo módulo), quando analisamos os diagramas acima.
Eliminação de concavidades
Os contornos críticos em volta do pilar devem ser convexos. O primeiro perímetro crítico consiste então no contorno do pilar com as concavidades removidas:
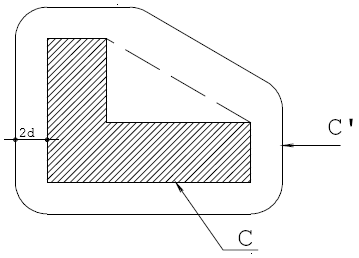
Perímetros efetivos
Os perímetros críticos são definidos conforme consta na ABNT NBR 6118. Mas o comprimento real usado no cálculo de tensões será limitado por arredondamentos de raio 2d e pela distribuição das armaduras de punção (que serão previamente planejadas). As projeções das linhas de armaduras em torno do pilar sobre o perímetro crítico podem ter distância máxima de 2d, limitando o comprimento do perímetro como na figura:
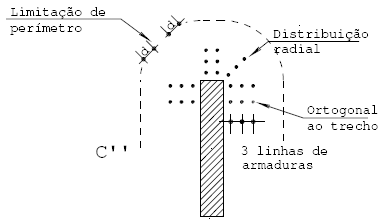
O resultado é que novos perímetros podem não ter um acréscimo significativo no comprimento, conforme a disposição das armaduras. Isto pode provocar um aumento no número de perímetros necessários para armar punção.
Critérios para controle dos perímetros críticos
O botão "Critérios de punção" chama a janela onde "Perímetros críticos" são os critérios para controle da geração dos perímetros. Os critérios são:

| Comprimento máximo para eliminação de concavidades | A remoção de concavidades só será feita em arestas com comprimento menor que o máximo definido aqui. |
| Comprimento máximo para agrupamento de trechos | É a distância Dmax mostrada anteriormente que serve para quebrar os sub-perímetros (padrão 1.5d). |
| Distância entre perímetros críticos paralelos | Por padrão vale 2d, conforme a norma. |
| Número de perímetros a mostrar inicialmente | Por padrão são gerados inicialmente três perímetros em volta do pilar. |
Adaptação de nomenclatura
Para maior clareza nas explicações a seguir, é necessário que alteremos a nomenclatura utilizada pela norma em relação aos índices. Desta forma, iremos utilizar o seguinte:

Com isso, a formulação passa a estar associada aos eixos cartesianos, o que torna muito mais simples o entendimento.
Cálculo do Wp
Uma das características básicas para o cálculo de punção é o módulo de resistência plástica (Wp).
O procedimento mais simples de utilizá-lo no sistema TQS é através da integral presente no item 19.5.2.2. da ABNT NBR 6118:2014:
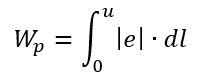
Esta integral pode ser tomada, de modo simplista como a somatória de comprimentos de aresta, do polígono analisado, multiplicados pela distância ao eixo analisado:
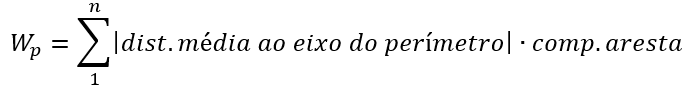
As arestas para esta soma devem considerar que o módulo da distância. Desta forma, toda poligonal deve ser “editada” de modo que sejam criados pontos na intersecção das arestas originais com as linhas de eixo que passam pelo CG. Um exemplo abaixo:
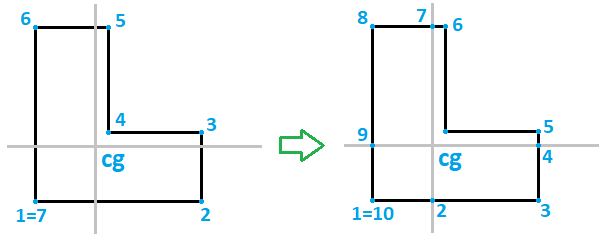
Observe que foram criados os pontos 2, 4, 7 e 9, que não existiam na poligonal original.
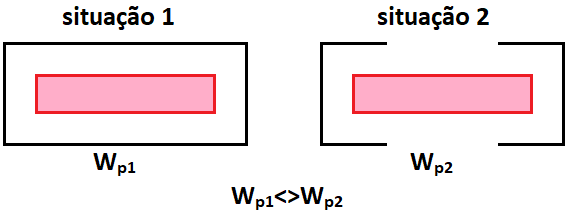
Uma observação muito importante é que o valor de é calculado sobre a geometria do perímetro crítico efetivamente existente. De modo gráfico temos:
Formulação genérica
A verificação a punção é feita através da tensão de cisalhamento, sendo apresentada a seguinte formulação na ABNT NBR 6118:
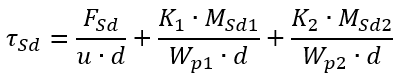
Adaptando esta fórmula para os eixos cartesianos X e Y, teremos a seguinte formulação:
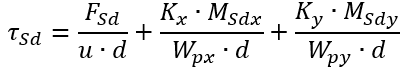
Onde:
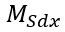 : momento fletor atuante em torno do eixo X analisado;
: momento fletor atuante em torno do eixo X analisado;
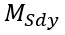 : momento fletor atuante em torno do eixo X analisado;
: momento fletor atuante em torno do eixo X analisado;
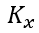 : é o valor de K (tabela 19.2 da ABNT NBR 6118:2014) obtido para relação
: é o valor de K (tabela 19.2 da ABNT NBR 6118:2014) obtido para relação 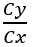 do pilar;
do pilar;
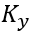 : é o valor de K (tabela 19.2 da ABNT NBR 6118:2014) obtido para relação
: é o valor de K (tabela 19.2 da ABNT NBR 6118:2014) obtido para relação 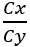 do pilar;
do pilar;
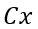 : dimensão em X do pilar. Usar retângulo envolvente, caso necessário;
: dimensão em X do pilar. Usar retângulo envolvente, caso necessário;
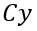 : dimensão em Y do pilar. Usar retângulo envolvente, caso necessário;
: dimensão em Y do pilar. Usar retângulo envolvente, caso necessário;
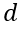 : altura útil da laje. Iremos utilizar a proposta do Eurocode 2, 2004:
: altura útil da laje. Iremos utilizar a proposta do Eurocode 2, 2004:
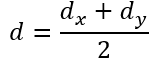
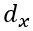 : altura útil da laje na direção X;
: altura útil da laje na direção X;
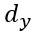 : altura útil da laje na direção Y.
: altura útil da laje na direção Y.
Não faz sentido fazer qualquer cálculo de punção com os valores 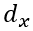 e
e 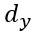 separadamente, uma vez que o efeito punção ocorre simultaneamente em ambas as direções e não pode ser separado em trechos.
separadamente, uma vez que o efeito punção ocorre simultaneamente em ambas as direções e não pode ser separado em trechos.
Observação sobre a formulação
A formulação apresentada no item 19.5.2.3.b, da ANBT NBR 6118:2014 está errada ao indicar que o valor de 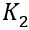 seria obtido com a substituição de
seria obtido com a substituição de 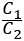 por
por 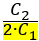 . O valor de
. O valor de 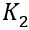 deve ser obtido com
deve ser obtido com 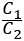 .
.
Esta formulação tem um formato muito próximo ao da tensão máxima em uma seção sujeita a flexão normal oblíqua. Apesar de não haver qualquer menção nas normas, podemos tomar a formulação com exatamente o mesmo entendimento. A primeira parcela está associada ao esforço normal. A segunda parcela, ao momento em torno do eixo X e a terceira parcela, ao momento em torno do eixo Y.
Esforços Solicitantes Utilizados
Modelo 6
Os esforços solicitantes a serrem utilizados na formulação apresentada representam o acréscimo de esforços solicitantes no pilar entre a base do pilar acima e o topo do pilar abaixo. Este acréscimo será considerado como vindo da laje e é para estes esforços que a verificação/dimensionamento de punção deve ser efetuado.
Modelo 4
No caso de o edifício ser processado com o Modelo IV, os esforços solicitantes são obtidos com base no modelo de grelha do pavimento.
Perímetro Crítico Excêntrico ao Pilar
Caso o baricentro do perímetro crítico não seja coincidente com o baricentro do pilar, é necessário alterar o momento fletor utilizado na formulação anterior. De modo esquemático, tomemos o pilar de canto a seguir:
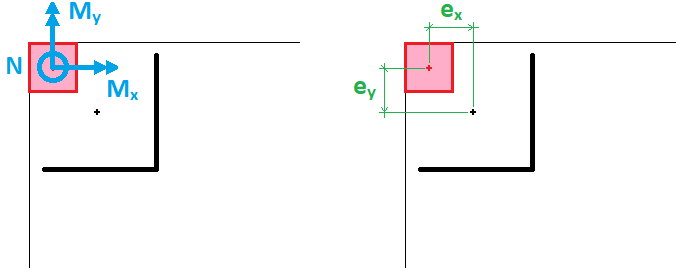
O valor de momentos fletores resultante da excentricidade são apresentados abaixo:
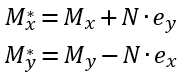
A formulação acima é diferente da apresenta pela ABNT NBR 6118 pois os valores de 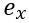 e
e 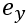 são tomados com seus sinais, assim como para os valores de
são tomados com seus sinais, assim como para os valores de 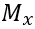 e
e 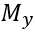 , de modo a manter a coerência vetorial dos momentos fletores.
, de modo a manter a coerência vetorial dos momentos fletores.
Na norma ABNT NBR 6118, a situação de perímetro crítico excêntrico é apresentada apenas para pilares de extremidade e de borda, mas, teoricamente, o mesmo problema ocorreria em pilares não retangulares.
O valor de momentos fletores "efetivos" a serem utilizados no cálculo de tensões é apresentado abaixo:
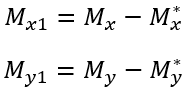
Pilares com Vigas
No caso de pilares que, além das lajes, também recebam vigas, a verificação/dimensionamento a punção é tratada da seguinte forma:
- Obtém-se os esforços solicitantes, como já mencionado;
- Subtrai-se os esforços que estão associados às vigas;
- Com isso, temos esforços solicitantes associadas apenas as lajes;
- Faz-se a verificação/dimensionamento.
Exemplos de cálculo
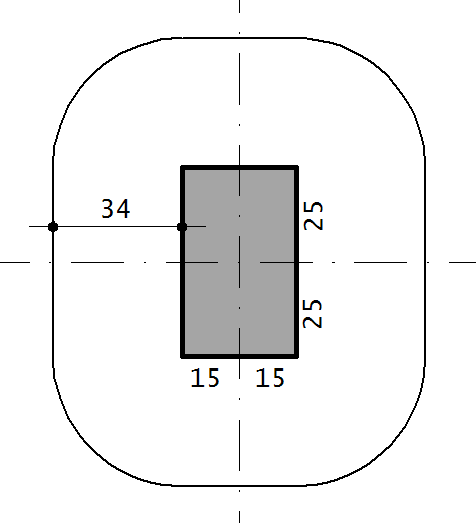
Considerando a situação hipotética apresentada abaixo:
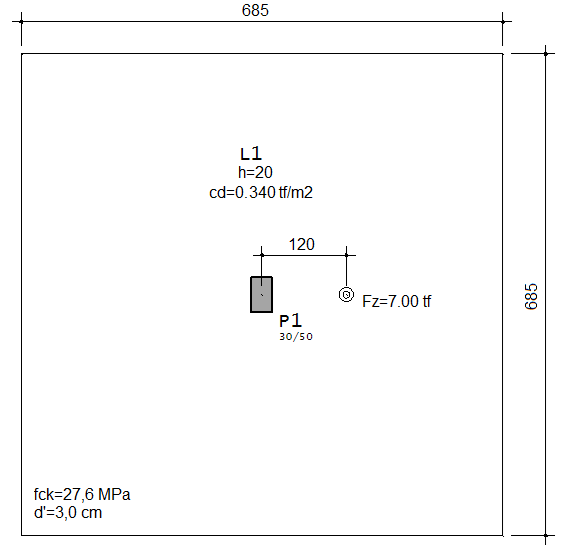
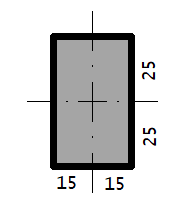
Do esquema acima temos:

Perímetro C
Os cálculos são os seguintes:

O valor apresentado pelo programa é o seguinte:
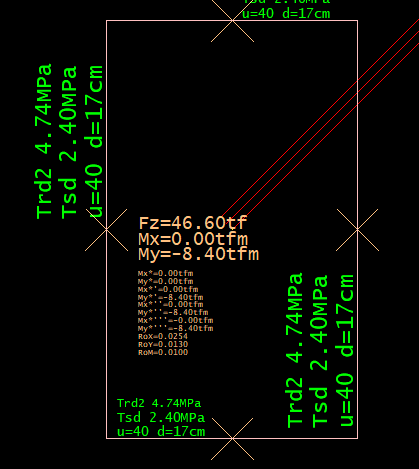
Perímetro C’
Os cálculos são os seguintes:
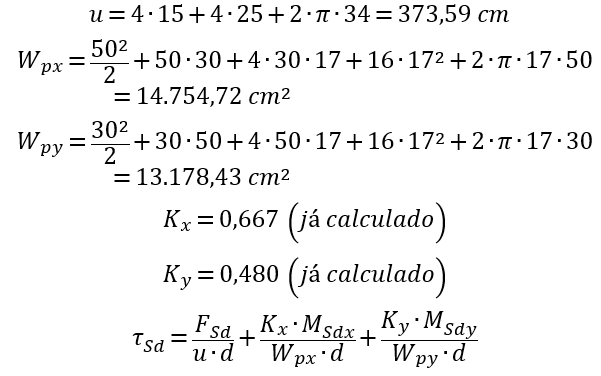
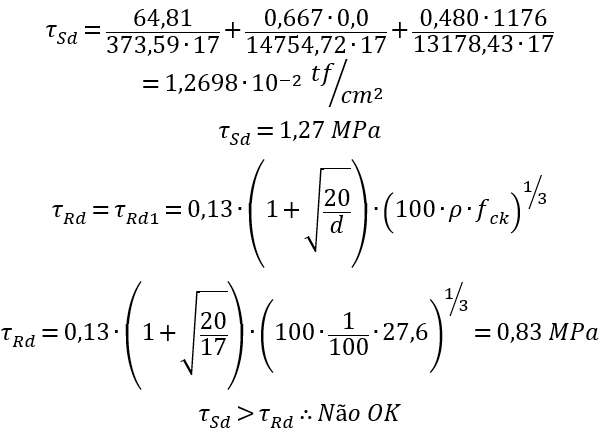
Obs: foi adotado 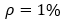 .
.
Então será necessário a utilização de armadura. Primeiramente, devemos definir a geometria onde a armadura será distribuída:
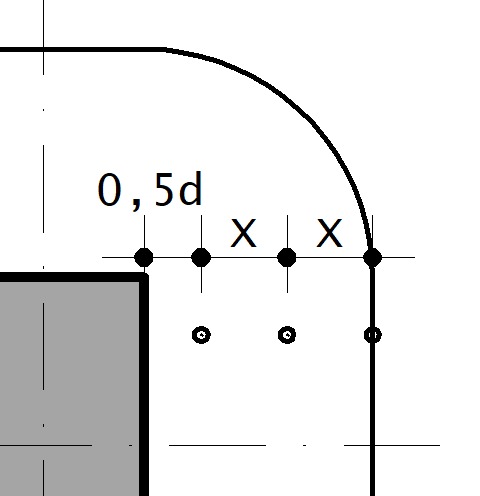
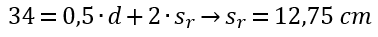
Conforme item 19.4.2:
| Espessura laje (cm) | fywd (MPa) |
| ≤ 15 | 250 |
| 17 | 333,75 |
| ≥ 35 | 435 |
Com isso:
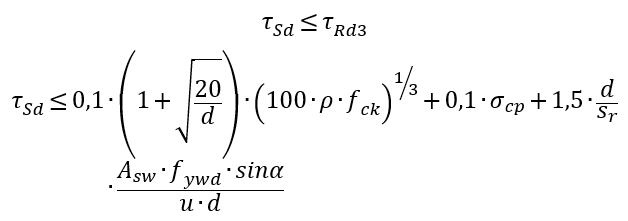
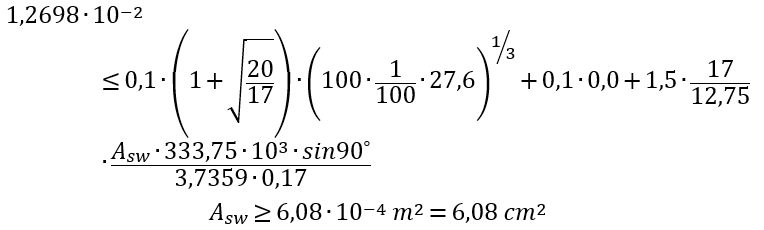
Considerando armadura com 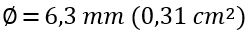 :
:
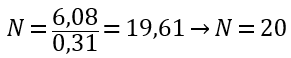
Ou seja, temos que distribuir 20 conjuntos de armadura de cisalhamento. No Editor é apresentado o seguinte:
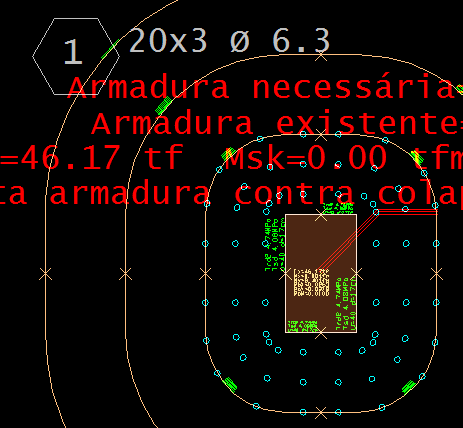
Perímetro C’’
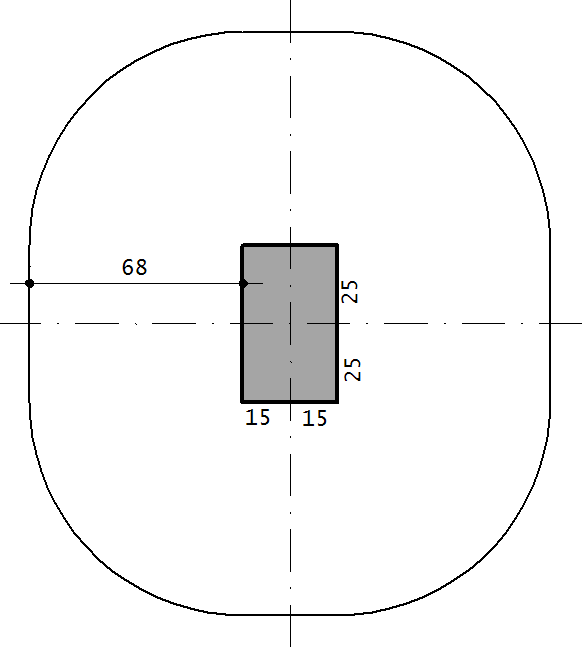
Os cálculos são os seguintes:

No Editor é apresentado o seguinte: