Interação: Fundações em Estaca e Solo (1/3)
Prezados Colegas da Comunidade
Devido ao interesse que o tema tem despertado e para maior esclarecimento dos participantes, vamos voltar ao assunto da interação entre os pilares, vigas e lajes de uma edificação usual, os elementos estruturais de fundação e o solo.
Neste caso vamos abordar a questão da fundação em estacas, especificamente uma estaca sob o pilar. Este é um caso interessante, pois o solo deve ser, obrigatoriamente, considerado para dar condições de estabilidade a estrutura.
Como já foi dito aqui nesta comunidade, este tipo de estrutura é, aparentemente, simples. Entretanto, cuidados especiais devem ser tomados, pois a análise conjunta entre a estrutura, estaca e presença do solo leva a considerações não muito intuitivas.
A análise feita está mais preocupada com os esforços solicitantes em todo o conjunto estrutura + estaca. Com a obtenção de solicitações satisfatórias, o dimensionamento e o detalhamento estrutural se tornam possíveis. É evidente que também fizemos as verificações estruturais necessárias para a estrutura e a estaca ( estabilidade, capacidade admissível da estaca, seção transversal adequada etc.)
O modelo abaixo é um modelo teórico. O principal objetivo é o de apresentar e raciocinar sobre este comportamento conjunto entre estrutura / fundações e solo. Além da estrutura de concreto armado em si, estamos também alimentando a sondagem do solo, características geométricas da estaca e critérios de projeto para determinação das vinculações elásticas (molas) na estaca representando o solo (teoria de Winkler).
Portanto, todas as variáveis acima são bem conhecidas do engenheiro estrutural com exceção dos critérios para determinação das molas. Para as molas verticais adotamos o cálculo da capacidade de carga da estaca através do processo Aoki-Lopes, processo bem conhecido de todos. O método Aoki-Lopes também considera e calcula o recalque da estaca para um determinado carregamento considerando o efeito das demais estacas (grupo). Com o recalque e a carga ao longo da estaca, basta dividir uma grandeza pela outra que obtemos as molas verticais distribuídas.
Para as molas horizontais a situação é mais indefinida. Temos dois processos básicos. Um deles depende da característica do material e o outro depende dos valores obtidos pelo SPT do terreno. Estamos adotando o método que depende do SPT, pois ele vai refletir melhor as variações das camadas do solo e medidas nas sondagens. Cabe aqui lembrar que, devido a imprecisão na obtenção destes valores, a representação do solo deve ser feita sempre com valores máximos e mínimos das grandezas e, posteriormente, adota-se uma envoltória final para o detalhamento.
Estamos empregando aqui o novo sistema computacional desenvolvido pela TQS e em fase de implantação em alguns clientes: SISEs. Neste novo sistema, para determinação dos coeficientes de mola (verticais e horizontais), basta fornecer os elementos da fundação, sondagens e selecionar os critérios de cálculo (envolve conhecimentos geotécnicos); a partir daí a estrutura é automaticamente discretizada e as molas calculadas automaticamente e introduzidas no modelo.
Descrição do projeto:
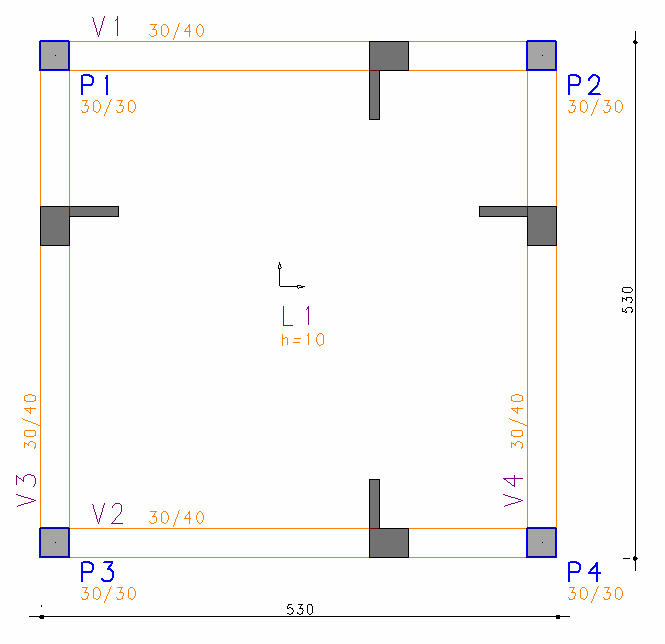
Superestrutura de 4 pavimentos, com 4 pilares quadrados (30 x 30 cm), lajes de altura 10 cm, com quatro vigas de 30 x 40 cm, em cada pavimento (com exceção da planta de fundação, em alguns casos), vãos de 5m.
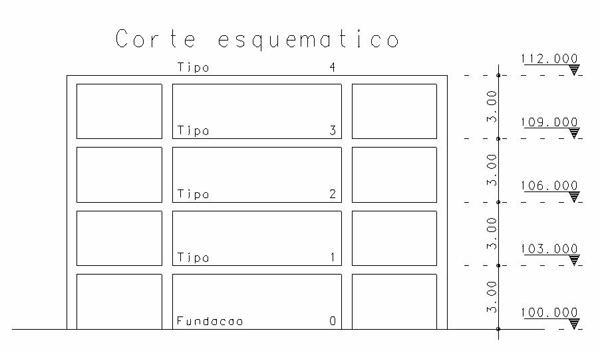
Dimensões típicas de cada pavimento:
Cargas consideradas nas lajes: ( 0,60 tf/m2: 0,25 [peso próprio] + 0.25 [perm.] + 0.1 [variav.]).
Considerados também 4 (quatro) carregamentos de vento, com as seguintes características:
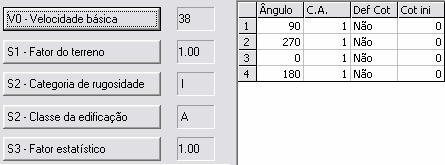
Sondagem:
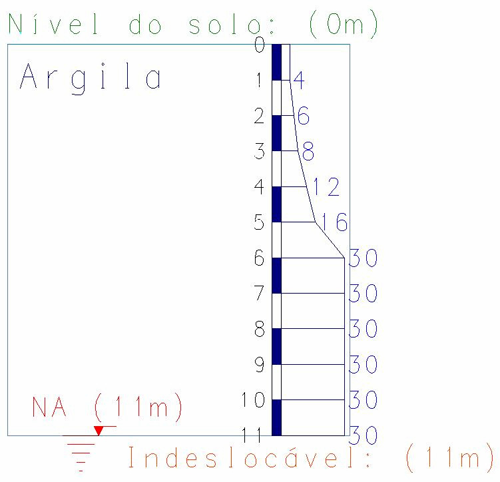
Estaca: Tipo hélice contínua, adotaremos uma tensão admissível ?adm = 40 kgf/cm² e fator de segurança = 2.0. Comprimento de 7 m.
Modelos Estudados:
A partir dos dados fornecidos, foram verificadas as dimensões necessárias para as seguintes condições de fundação (3 soluções propostas):
Solução 1 - Blocos sobre 1 estaca, SEM vigas-baldrame entre os blocos
Solução 2 - Blocos sobre 3 estacas, SEM vigas-baldrame entre os blocos
Solução 3 - Blocos sobre 1 estaca, COM vigas-baldrame, entre os blocos
Observe que, por se tratar de uma estrutura com simetria, nas duas direções, os resultados, apresentados aqui em uma direção (X), são análogos aos da outra direção (Y).
A seguir, os detalhamentos, alguns comentários e os resultados obtidos, para cada condição. Esta mensagem, devido a sua extensão apresentará apenas a solução 1.
Solução 1 - Blocos sobre 1 (uma) estaca, SEM vigas-baldrame entre os blocos:
1.1) Coeficientes de Mola Sem Majoração
Para esta condição, os momentos fletores, oriundos da superestrutura, precisam ser absorvidos pela fundação – as estacas, visto que cada pilar está ligado diretamente com o seu devido elemento de fundação. Nestes termos, verificou-se a dimensão mínima destas estacas: Ø = 60 cm, para eliminar os avisos de capacidades de carga, tensões excedidas, deslocamentos limites, instabilidades da estrutura, etc.
Daí a necessidade das estacas serem armadas, para combate aos esforços devidos às flexões, transmitidos às estacas através dos blocos de fundação, cujas armaduras também devem ser dimensionadas e detalhadas.
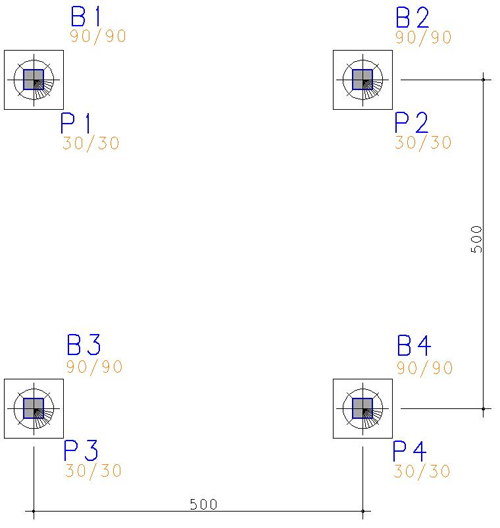
Modelo da fundação em planta (sem travamento)
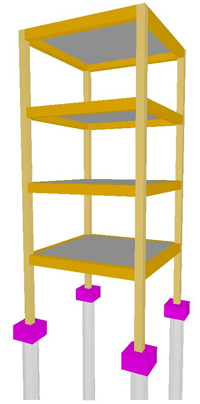
Modelo 3D de toda estrutura + estacas
O pórtico espacial resultante, para este caso, será como o que segue abaixo, onde se observa a infra-estrutura discretizada e agregada à superestrutura (através de novos nós e vínculos elásticos), formando-se então um novo pórtico espacial - um modelo integrado e único – com a presença do efeito do solo:
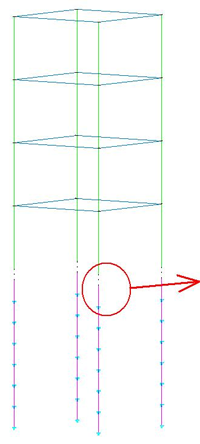 <br/> Pórtico espacial com a infra-estrutura agregada. <br/> Pórtico espacial com a infra-estrutura agregada. | 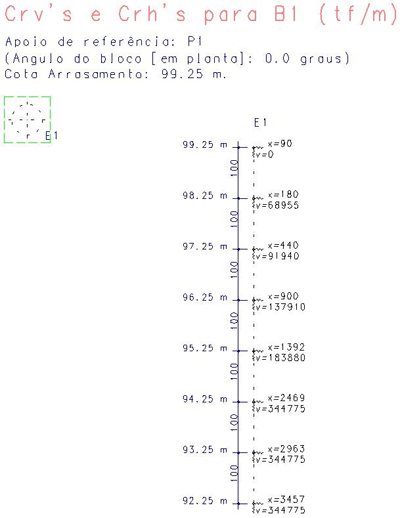 <br/>Detalhe representativo dos vínculos elásticos que representam o solo ao longo da estaca. <br/>Detalhe representativo dos vínculos elásticos que representam o solo ao longo da estaca. |
Os principais resultados obtidos podem ser verificados graficamente, tanto na visualização do Pórtico espacial (esforços e deslocamentos), quanto nos desenhos que o SISEs, nos fornece, de forma concisa:

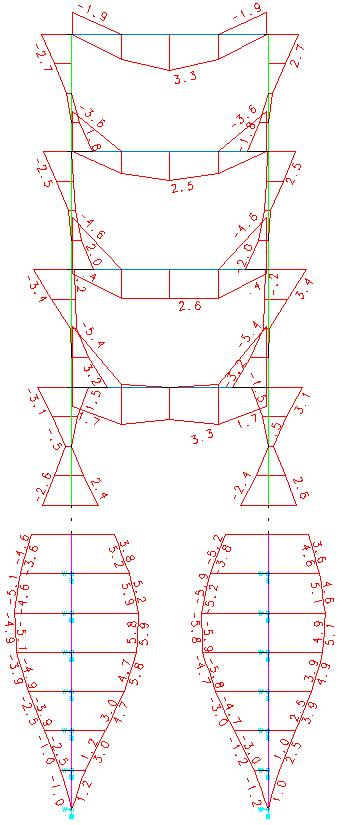
Detalhe de visualização de diagramas, pelo pórtico espacial, específico para o esforço (My) e carregamento acima (envoltória).
Deve-se notar que o momento fletor na estaca foi maior do que no pilar. Sem a colaboração da estaca a flexão, a estrutura não fica estável. As armaduras do pilares devem ter emendas com as armaduras das estacas. Não estamos estudando ainda os efeitos de segunda ordem do conjunto pilar + única estaca.
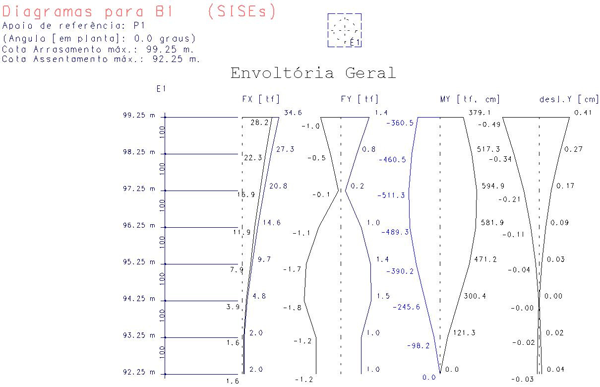
Desenho gerado pelo SISE, com os resultados (esforços e deslocamentos, selecionáveis pelo usuário) para o Bloco B1.
Observe pelo diagrama acima que o momento fletor máximo na estaca não está no topo e sim num ponto intermediário, igual a 594.9 tf*cm, que corresponderia a uma armadura de As = 11.23 cm² (14 Ø 10 mm). Portanto, sob o ponto de vista do concreto, a estaca passou, armada. Com esta magnitude de momentos fletor a estaca tem regiões de tração. Sob o ponto de vista do solo, a capacidade de carga da estaca atendeu plenamente.
Algumas verificações simples sobre a estabilidade do modelo integrado (com a interação Solo- Estrutura):
- Coeficientes Gama Z (?z ): 1.084
- Deslocamentos Horizontais: 0.64 cm (H/1883), entre pavimentos: 0.19 cm (Hi/1573.)
Para estacas com diâmetros inferiores a Ø = 60 cm, não se consegue, através deste modelo, obterse como resultado uma estrutura estável. O sistema acusa coeficientes de Gama Z (?z) elevados, deslocamentos horizontais globais e entre pavimentos excessivos, etc. Portanto, sem elementos de travamento na fundação, necessita-se de estacas de diâmetro Ø = 60 cm, armaduras nas estacas e o comprimento destas armaduras em quase toda a estaca. Não estamos estudando aqui com profundidade os métodos construtivos para a execução desta armadura.
1.2) Coeficientes de Mola Aumentados em 10X
Conforme também já comentado, vamos apresentar abaixo os diagramas de momentos fletores no conjunto estrutura/fundação com os coeficientes de mola nas estacas multiplicados por 10 vezes:
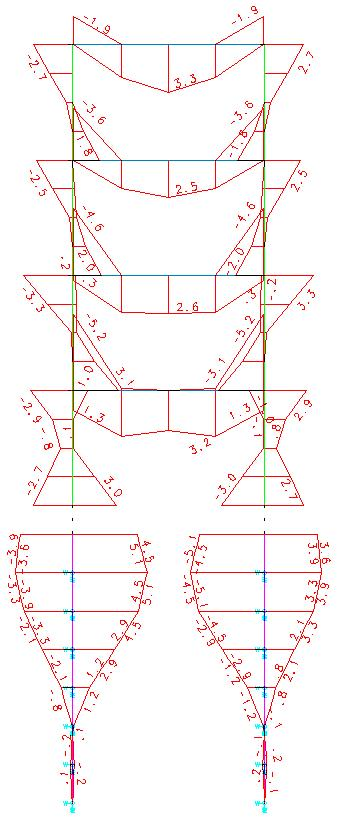
A primeira observação a ser feita é que o aumento do vínculo elástico horizontal em 10 vezes não alterou significativamente os resultados de momentos fletores. Com o maior engastamento da estaca no solo, os momentos fletores na estaca se reduziram. Mesmo assim é necessária a armação nas estacas. Os momentos fletores na base do pilar aumentaram.
1.3) Pilar Articulado e Coeficientes de Mola Normais
Muitos colegas acham que simplesmente articular a base do pilar resolve o problema dos momentos fletores na estaca. Vamos apresentar abaixo o mesmo diagrama de momentos fletores para este caso.
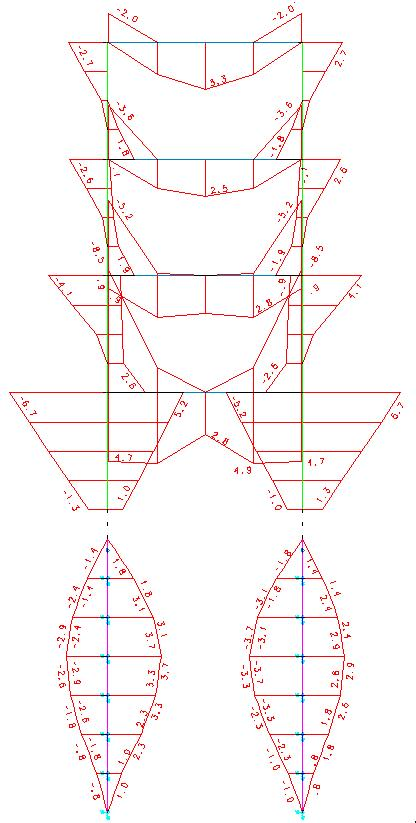
No diagrama acima dá para notar que os momentos fletores positivos no pilares e na viga do primeiro pavimento do pórtico aumentaram e o que é o principal: os momentos fletores na estaca não foram eliminados. Devido a componente horizontal da força na base do pilar, os momentos fletores aparecem ao longo do fuste do pilar. Apenas no topo da estaca o momento fletor é nulo. O edifício também sofreu deslocamentos horizontais maiores e o Gama Z aumentou. Esta solução também não é uma boa solução. A estaca também necessita ser armada.
Aproveitando a oportunidade, vale aqui lembrar também de outra observação interessante que, infelizmente, não é tão rara quanto se pensa: a passagem dos valores de cargas da estrutura para a fundação considerando apenas a carga vertical. Se a estrutura é engastada a rotação e a translação horizontal, a presença de momentos fletores e forças horizontais são fundamentais para o seu equilíbrio. Se a fundação não for projetada para tais solicitações, todo o conceito de projeto está deficiente com conseqüências imprevisíveis.
1.4) Estrutura Engastada ( sem fundação projetada)
Observe os diagramas a seguir para este mesmo projeto, considerando as bases dos pilares com “engaste perfeito”.
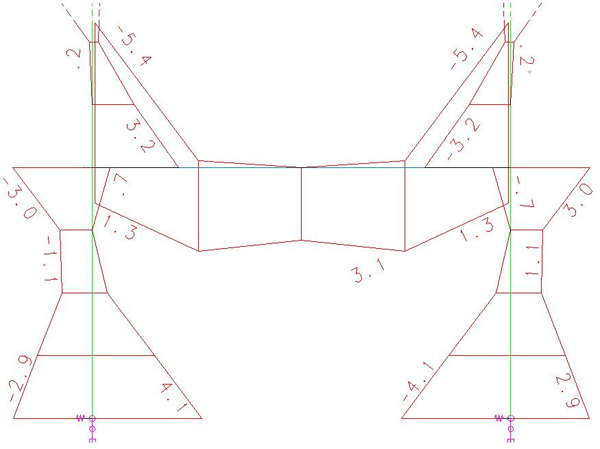
Detalhe da envoltória dos momentos My (base dos pilares e 1º. lance), considerando o pórtico da estrutura com “engastamentos perfeitos”.
Qual o tipo de fundação mais adequado que deveria ser considerado para se respeitar este “modelo”? Já vimos neste tópico que a estaca isolada não é uma das melhores soluções. Em mensagens posteriores vamos analisar outras possíveis soluções.
Nelson Covas
Nilson Oliveira S.
TQS – São Paulo – SP.
