Interação: Fundações em Estaca e Solo (2/3)

Prezados Colegas da Comunidade

Seguindo o assunto da Interação entre estrutura, fundação e solo, vamos apresentar agora uma outra possível solução, tendo sempre como meta a estabilidade da estrutura, a adequação e uma melhor correspondência entre o modelo analisado e a estrutura real.

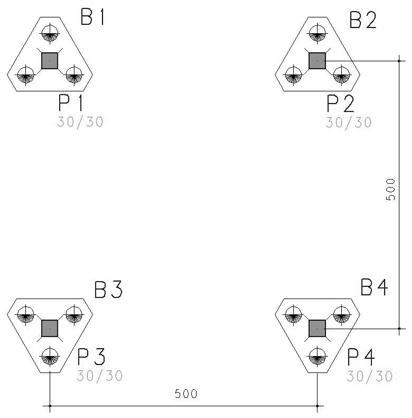
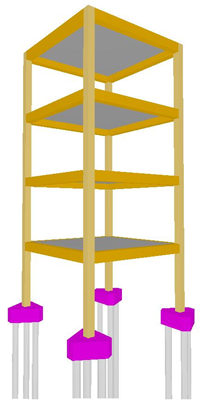
Solução 2 - Blocos sobre 3 (três) estacas, SEM vigas-baldrame entre os blocos:

Para esta condição também, os momentos fletores, oriundos da superestrutura (de acordo com as ações consideradas no projeto), precisam ser absorvidos pela fundação – as estacas. Porém, neste caso específico, os efeitos das flexões podem ser “transformados” em binários (forças de reação, nas estacas, que se contrapõem a cada esforço de flexão, transmitido ao bloco de fundação), em ambas as direções.

Verificou-se a dimensão mínima destas estacas Ø = 30 cm, de forma a atender as exigências de cargas e tensões admissíveis.

O espaçamento entre as estacas é de 90 cm, para anular possíveis esforços resultantes de tração, em qualquer estaca.

2.1) Caso: Coeficientes de mola sem majoração

Como descrito anteriormente, para que o modelo considerasse que os esforços de flexão fossem, a priori, “convertidos” apenas em binários nas estacas, definimos neste modelo articulações no topo (interface entre a estaca e o bloco de fundação) de cada estaca.

Observe porém que, de acordo com os diagramas a seguir, ainda apareceram momentos fletores nos pontos intermediários das estacas discretizadas, decorrentes da aplicação da força horizontal do pórtico na base do pilar e da ação/reação entre as estacas e o solo.

De acordo com critérios pré-definidos, pelo sistema SISEs, as verificações de capacidade de carga, tensões admissíveis e ocorrência de tração, por estaca, são automaticamente efetuadas pelo sistema e incluídas nas mensagens de avisos e erros.

O diagrama de momentos fletores para toda a estrutura (super e infra) é apresentado abaixo. Unidades: tf*m.

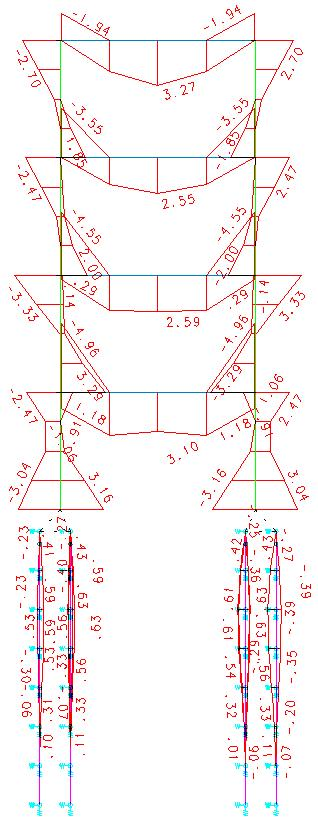
Algumas verificações simples sobre a estabilidade do modelo integrado (com a interação Solo- Estrutura):

• Coeficientes Gama Z (?_z): 1.059
• Deslocamentos Horizontais: 0.46 cm (H/2592), entre pavimentos: 0.12 cm (Hi/2493.)

O comportamento da estrutura melhorou significativamente com o “engastamento” na base dos pilares se comparado com a solução anterior de uma estaca por pilar.

Como se pode notar pelo diagrama acima, as estacam ainda estão submetidas a esforços de flexão. O valor máximo do momento fletor foi de 62.8 tf*cm a 2 m de profundidade. Na seção transversal da estaca a esta profundidade, temos ainda tensões de tração na borda da estaca. A estaca também necessita ser armada até uma determinada profundidade. O As calculado para a estaca é de: 2.83 cm² [4 Ø 10 mm].

2.2) Caso: Coeficientes de mola majorados em 10X

O diagrama de momentos fletores para toda a estrutura (super e infra) é apresentado abaixo. Unidades: tf*m.

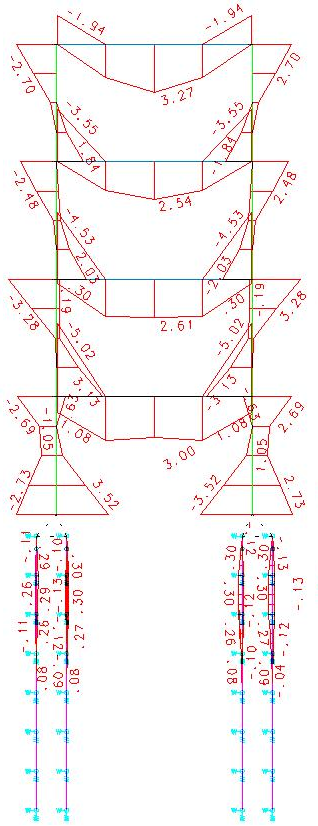
Como se pode notar pelo diagrama acima, as estacam ainda estão submetidas a esforços de flexão. O valor máximo do momento fletor foi de 30.2 tf*cm a 1 m de profundidade. Na seção transversal da estaca a esta profundidade, temos ainda tensões de tração na borda da estaca. A estaca também necessita ser armada até uma determinada profundidade.

2.3) Caso: Coeficientes de mola infinitos

Para simular o que é feito na prática de projeto neste caso e poder comparar com os resultados obtidos no sistema, vamos aumentar os vínculos elásticos / coeficientes de mola para um valor muito alto (infinito).

O diagrama de momentos fletores que obtivemos é o abaixo.

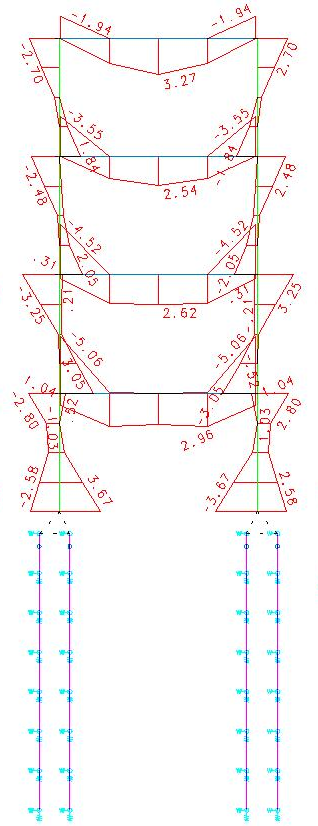
Podemos observar que os momentos fletores nas estacas desapareceram. A força horizontal que aparece na base do pilar da estrutura é absorvida no topo da estaca na sua totalidade. A estaca agora não necessita mais de armação pois ela não apresenta nenhum ponto de tração ao longo da sua extensão.

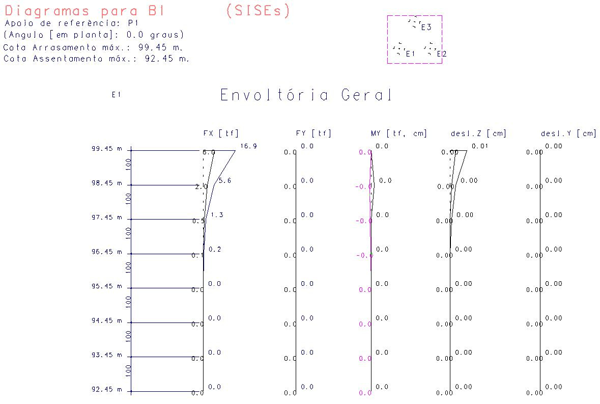
Detalhe de desenho, gerado pelo SISEs, com os resultados (esforços e deslocamentos) principais em uma estaca.

Este é o procedimento adotado por muitos engenheiros quando a força horizontal no pé do pilar é desprezada. Será esta a condição real de comportamento da estrutura? Será que os diagramas apresentados nos itens 2.1 e 2.1 não são mais verdadeiros? É uma questão a ser analisada.

Saudações

Nilson Oliveira Silva

TQS - SP