Redução de capacidade de carga de estaca agrupada
- Nelson Covas
TQS Informática – Sistemas Computacionais/ Engenharia Estrutural
Rua Pinheiros, n 706 c/02 - CEP 05422-001, São Paulo, SP, Brasil
- Valério S. Almeida
Departamento de Engenharia Civil, Universidade Federal de Ouro Preto
Campus Universitário – Ouro Preto – MG – Brasil
Sumário
A consideração da deformabilidade do solo no projeto de edifícios em concreto armado é um tema tratado no meio acadêmico e em escritórios de engenharia estrutural há décadas. Entretanto, no Brasil não existia, até então, um sistema computacional que fosse capaz de oferecer ao usuário um ferramental que simule a interação solo-estrutura de maneira prática, eficiente e com nível de respostas confiável do ponto de vista acadêmico e prático. Neste intuito, a empresa TQS Informática Ltda vem desenvolvendo um modelo numérico denominado SISEs – Sistema de Interação Solo-Estrutura. O modelo consiste em um sistema que acople o edifício 3D, a infra-estrutura e o maciço de solos. O edifício é baseado nas normas técnicas de concreto armado e na metodologia usual de elaboração e representações de projetos estruturais empregados no Brasil. Os elementos de fundação simulam as fundações diretas (sapatas, radiers) ou profundas (estacas e tubulões) e o maciço de solos pode ser representado como um meio não – homogêneo com a cota do indeslocávelprescrita, a priori, pelo usuário. Assim, este artigo tem apenas o objetivo de analisar as sapatas isoladas ou em grupos, comparando as respostas obtidas pelo SISEs/TQS com formulações presentes na literatura advindas de outras técnicas numéricas, tal como método de elementos finitos ou método de elementos de contorno, sendo um passo inicial paravalidar o modelo de interação solo-fundação para posteriores análises mais gerais na interação entre solo-fundação-edifício que devam ser descritas em trabalhos futuros.
1. INTRODUÇÃO
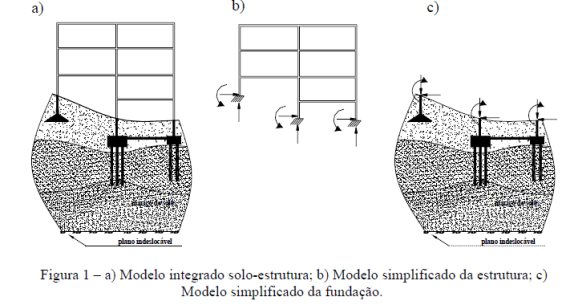
O edifício, em conjunto com o maciço de solos, representa um sistema mecânico integrado único. As ações que ocorrem na superestrutura são transferidas para o solo, mobilizando este, o qual se deforma e define uma configuração de equilíbrio para o conjunto estrutura/solo, Fig. 1.a. Entretanto, este mecanismo integrado, ou mais especificamente a inter-relação entre a super, infra e subestrutura e o maciço de solos, de modo geral, é analisada de forma independente. Na prática, a análise do edifício é tomada considerando-se os pilares engastados em sua base, conforme Fig. 1.b, gerando reações que posteriormente são transferidas ao projetista de fundações que usa estes valores para dimensionar e verificar seus elementos de fundação, Fig. 1.c.
Esta simplificação de projeto advém do alto grau de complexidade para avaliar o conjunto mecânico integrado. Pois cada um dos subsistemas já representa um vasto campo de estudo, quer na variabilidade de parâmetros físicos e geométricos, quer nas correspondentes idealizações dos modelos mecânicos. Somando-se a isto, os diferentes ramos de interesse e de conhecimento dos projetistas e pesquisadores nesta área são voltados para referenciais diferentes.
Por um lado, o projetista de fundações analisa a complexa integração entre a subestrutura e o maciço de solos, como a determinação da capacidade de carga de estacas ou o cálculo das tensões de ruptura das sapatas, que estão submersas em solos estratificados ou colapsíveis, expedientes previstos pela norma de Projeto e Execução de Fundações do Brasil, NBR 6122 (1996). O projetista não considera as mudanças de configurações que estes perfis de solo provocam na superestrutura levando a um estado de tensões e recalques não previstos no sistema subestrutura/maciço, projetado então de forma desacoplada com a superestrutura.
Em contrapartida, o projetista estrutural está voltado para os efeitos que ocorrem na superestrutura, como por exemplo, a consideração do fenômeno de não-linearidade geométrica (efeito de 2ª ordem) ou o comportamento não-linear do material que o edifício está sujeito, onde ambos os procedimentos devem ser avaliados por força da norma de Projeto de Estruturas de Concreto do Brasil, NBR 6118 (2000). Sendo que o projetista também não leva em conta os efeitos que o meio de apoio está sujeito quando da absorção das ações, e nas posteriores modificações da superestrutura que possa acarretar nas vigas, pilares, etc.
Para o caso da avaliação qualitativa e quantitativa dos edifícios de forma isolada, ou seja, sem a consideração do maciço, na literatura existem diversos modelos para análise de maneira criteriosa seu comportamento. Citam-se os trabalhos de Pinto (2002), Chan et al. (2000), Franco (1995), Vecchio & Emara (1992), Pimenta & Yojo (1992) e Franco & Vasconcelos (1991), onde todos são aplicados no campo da análise não-linear geométrica. Para o caso da análise não-linear física, têm-se os trabalhos de Oliveira (2001), Martins (2001) e Kim & Lee (1993) que introduzem o efeito plástico nas lajes e vigas do edifício. Martins (2001), Smith & Coull (1991) e Taranath (1988) analisam edifícios com núcleos resistentes.
Nota-se que os modelos empregados para representar o edifício são enriquecidos a cada dia, onde além de considerar os seus efeitos não-lineares, também são incorporadas a influência das lajes, do núcleo estrutural e até a presença da alvenaria para a melhor avaliação de seu comportamento estrutural, Holanda Jr. (2002) e Mamaghani et al. (1999).
Entretanto, uma análise mais criteriosa sobre o comportamento do edifício deve também considerar, além da inclusão destes efeitos citados anteriormente, a influência da deformabilidade do maciço onde a superestrutura se apoia. Neste sentido, existem várias pesquisas voltadas neste estudo. Lopes & Gusmão (1991) investigaram o desenvolvimento de recalques de um pórtico apoiado em um meio elástico semi-infinito, empregando os procedimentos de Mindlin (1936). Este pórtico representava um edifício de concreto armado e estava sujeito apenas a carregamento vertical.
Ramalho & Corrêa (1991) estudaram o comportamento de edifícios apoiados em meio elástico semi-infinito e homogêneo, considerando os elementos de fundações apenas do tipo sapata. O solo foi representado pelo Método de Elementos de Contorno (MEC) e as sapatas foram representadas pelo Método de Elementos Finitos (MEF). Neste modelo são inseridas as ações de vento. Noorzaei et al. (1993) avaliam as respostas de um pórtico plano apoiado em um meio não-homogêneo e considerando-se a não-linearidade física do pórtico.
Uma maneira mais criteriosa de avaliar o maciço é possibilitando a inclusão de uma camada indeslocável a uma distância indicada em projeto, uma vez que os modelos, de modo geral, partem da hipótese de que a camada indeslocável está a uma distância infinita, não levando em conta a possível presença de rochas no maciço. Somado a esse fator, a consideração do maciço como um meio não-homogêneo pode levar a um modelo mais próximo das condições reais de campo, uma vez que a origem do maciço advém de transformações geológicas que não geram propriedades homogêneas ao meio contínuo. Nesta linha, alguns modelos também têm levado em conta estas condições, por exemplo, os trabalhos de Moura (1995), Reis (2000), Romanel et al. (2000), Romanel & Kundu (1990), Gusmão (1990), Antunes & Iwamoto (2000), Holanda Jr. (1998) e Almeida & Paiva (2004).
Porém os trabalhos citados possuem restrições quanto a sua aplicabilidade. Alguns não permitem a inclusão de elementos de fundação, outros só consideram ações verticais no edifício, um outro grupo representa a não-homogeneidade e a camada indeslocável, mas não considera o edifício com efeito de 2ª ordem ou de geometria qualquer.
Como consequência, é lícito afirmar que todos os trabalhos citados acima abordam de forma superficial e com pouca praticidade uma aplicação real de projeto, pois todos possuem restrições, quer no tocante a modelos mecânicos do edifício integrado com o maciço, quer na difícil usabilidade para o lançamento da geometria do edifício ou dos perfis geológicos das sondagens, quer em inexistir um gerador de malha ou visualizador de resultados adequado para o usuário. Soma-se também ao fato destes trabalhos não avaliarem de maneira completa todos os elementos estruturais quanto aos Estados Limites de Serviço e Último em função das normas correntes de Execução de Estruturas de Concreto Armado do Brasil, NBR 6118 (2000) e de Fundações, NBR 6122 (1996).
Neste intuito, a empresa TQS Informática Ltda vem desenvolvendo um modelo numérico denominado de SISEs, Sistema de Interação Solo-Estrutura, que se configura em um modelo que acopla o edifício 3D, a infraestrutura e o maciço de solos. O edifício é baseado nas normas técnicas de concreto armado e na metodologia usual de elaboração e representações de projetos estruturais empregados no Brasil. É possível também considerar os efeitos de 2ª ordem e a não-linearidade física no pórtico espacial. Os elementos de fundação simulam as fundações diretas (sapatas isoladas, associadas e radiers) ou profundas (estacas e tubulões) e o maciço de solos pode ser representado como um meio não – homogêneo com a cota do indeslocável prescrita, a priori, pelo usuário.
Assim, neste artigo é apresentado a metodologia empregada para a modelagem dos elementos de fundações e do maciço de solo, mostrando algumas comparações numéricas de sapatas isoladas entre as análises feitas pelo SISEs/TQS e outras formulações presentes na literatura clássica, pretende-se apenas validar neste primeiro artigo os modelos que simulam as fundações rasas, para futuras análises em sistema de interação solo-estrutura mais complexos.
2. A TQS E O SISTEMA CAD/TQS
A TQS Informática Ltda é uma empresa de desenvolvimento de sistemas computacionais gráficos e de cálculo para engenharia estrutural. O desenvolvimento destes sistemas computacionais foi baseado nas normas técnicas de concreto armado e na metodologia usual de elaboração e representações de projetos estruturais empregadas pelas empresas brasileiras.
Os sistemas CAD/TQS fazem o cálculo das solicitações dos elementos de viga, pilar utilizando elementos de pórtico espacial e as lajes pelos processos de grelha equivalente ou por elementos finitos planos. Inclui também a análise de estabilidade, dimensionamento, detalhamento e desenhos de formas, vigas, pilares, lajes (convencionais, nervuradas, planas e cogumelos), blocos e sapatas. Para elementos especiais (pontes, muros, escadas, pré-moldados) tem-se um editor gráfico exclusivo e orientado para o detalhamento de armaduras.
Para lajes e vigas o sistema também possibilita a utilização de concreto protendido.
Os sistemas CAD/TQS não dependem de outros sistemas computacionais gráficos de editoração de desenhos. Foi desenvolvido um editor gráfico próprio, totalmente incorporado aos sistemas CAD/TQS, voltado à engenharia estrutural, onde o usuário lança a estrutura, visualiza resultados, edita armaduras, emite os desenhos em impressora ou traçador gráfico, etc. Este editor é um dos principais motivos da abrangência e produtividade dos sistemas CAD/TQS. O desenvolvimento dos métodos de cálculo do edifício espacial com os demais elementos existentes é baseado no Método de Elementos Finitos, Soriano (2003).
3. SISTEMA DE INTERAÇÃO SOLO-ESTRUTRA DA TQS
Atualmente, a TQS está em fase de finalização do SISEs, Sistema de Interação Solo-Estrutura, que é um sistema computacional bastante abrangente para a análise da interação estrutura-solo, onde se aproveita todas as ferramentas de cálculo, lançamento e editoração já existentes no CAD/TQS.
Com este intuito, lança-se graficamente o edifício, realiza-se a geração adequada e automática dos carregamentos de uma estrutura dos sistemas CAD/TQS, conforme preconiza a norma brasileira NBR 6118. Assim, dezenas de combinações de carregamentos são criadas, processadas e enviadas ao geotécnico para a elaboração do projeto de fundações junto ao modelo da superestrutura. Entretanto, este elevado volume de informações, embora correto do ponto de vista técnico, continua trazendo problemas para o engenheiro geotécnico na elaboração do projeto dos elementos de fundações, pois este não estava acostumado a analisar a fundação considerando estes elevados números de combinações. Neste sentido, o SISEs/TQS vem a abrir também muitas possibilidades para pesquisa nesta frente.
A filosofia básica do SISEs/TQS consiste no seguinte:
1. O modelo básico lançado pelo engenheiro estrutural envolvendo os diversos materiais, a geometria e os carregamentos, são passados ao engenheiro geotécnico;
2. O engenheiro geotécnico alimenta no sistema as diversas sondagens realizadas no terreno;
3. São selecionados os tipos de fundações (rasa e/ou profunda) mais adequadas para o projeto, podendo haver tipos de elementos diferentes num mesmo projeto: estacas, radiers e tubulões;
4. As dimensões dos elementos de fundação (sapatas, radiers, estacas, tubulões, etc.) são pré-dimensionadas pelo geotécnico;
5. Estes elementos são lançados no SISEs/TQS junto aos respectivos pilares advindos do modelo estrutural;
6. São selecionados critérios de projeto para a simulação da presença do solo junto aos elementos de fundação (capacidade de carga em estaca, métodos para cálculo de recalques em sapata, etc);
7. São calculados os coeficientes de influência do solo em cada ponto discretizado da fundação e anexados ao modelo estrutural da fundação, conforme as diversas metodologias disponíveis na literatura e implementadas no SISEs/TQS;
8. O SISEs/TQS cria um novo modelo estrutural contendo toda a superestrutura em conjunto com os elementos de fundação, discretizados convenientemente e com a influência do solo já integrada. Este novo modelo é resolvido, possibilitando todos os recursos disponíveis no CAD/TQS, como por exemplo à consideração da análise não-linear geométrica (P- Δ );
9. O engenheiro geotécnico analisa os resultados para todas as condições de carregamentos para verificar a adequação dos elementos de fundação adotados com as tensões de ruptura, a capacidade de carga do solo e os recalques máximos mobilizados;
10. Se necessário, ajustes nos elementos de fundação são realizados e o processo é refeito até que a solução desejada, do ponto de vista de tensões de ruptura e recalques seja atingida;
11. O novo modelo integrado solo-estrutura é repassado ao engenheiro estrutural, o qual avalia as respostas nos elementos estruturais (vigas, pilares, lajes, etc) e, caso necessite, altera alguma propriedade do material ou geometria de qualquer elemento. Ele reprocessa o modelo solo-estrutura até atingir uma configuração de projeto conveniente;
12. O modelo pode ser repassado ao geotécnico, que reavalia a nova distribuição de esforços e recalques na fundação. Esta interatividade, totalmente automatizada no sistema TQS entre os profissionais, pode ser feita até que uma condição ótima seja atingida para ambos.
3.1 Elementos de fundação do SISEs/TQS
O SISEs/TQS disponibiliza os seguintes tipos de elementos de fundação para a modelagem da fundação:
a. Sapatas Isoladas;
b. Sapatas Associadas, com e sem furos existentes;
c. Radiers, com e sem furos existentes;
d. Estacas: circulares, quadradas, retangulares (Barrete) sob bloco rígido ou flexível;
e. Tubulão: fuste e base circular;
Convêm destacar que todos os elementos de fundação são modelados pelo Método de
Elementos Finitos com elementos lineares com as funções de forma de flexão (polinômio completo do 3º grau), normal e torcional (ambos com polinômio completo do 1º grau) ou seja, um elemento finito de pórtico espacial convencional.
A simulação das sapatas (isoladas ou associadas), radiers e dos blocos só é possível com sua geometria retangular.
Para todos os elementos de fundação, no SISEs/TQS é necessário definir certos parâmetros de projeto, como: dimensões, espessura, ângulo de inclinação em planta ou em corte, valor da resistência do concreto, cota de assentamento e de arrasamento, peso próprio, grau de refinamento para geração da malha de elementos finitos, dentre outros parâmetros de projeto, os quais são detalhados no manual do sistema. O SISEs/TQS insere automaticamente todos os elementos de fundação no modelo do edifício.
3.1.a. Sapatas Isoladas
A representação dos elementos de sapata isolada é feita associando-se um certo pilar do edifício a sapata, veja Fig. 2. Para este elemento, só é possível representá-lo com geometria retangular.
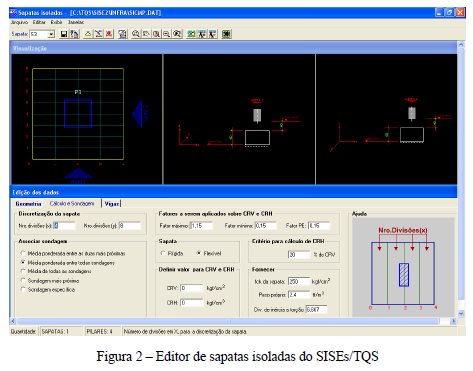
3.1.b. Sapatas Associadas e Radiers
No editor de fundação, para cada radier ou sapata associada, pode-se definir dois tipos de regiões: Sapata Contígua Retangular (SCR) e Região Complementar Retangular (RCR). Para o primeiro caso, é necessário associar um pilar da superestrutura a esta região, enquanto que em RCR não é possível associar um pilar a ela. Em cada caso, pode-se definir uma altura específica. Da mesma maneira que a sapata isolada, é apenas possível representá-lo com geometria retangular, veja Fig. 3.
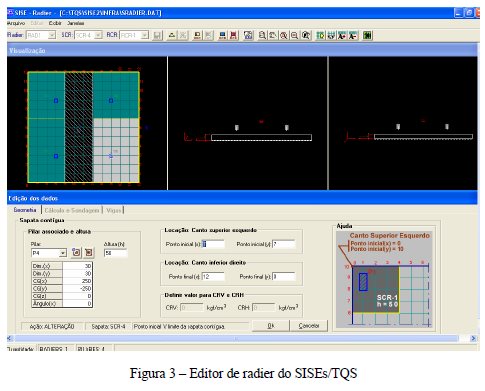
3.1.c. Fundação Profunda: Estacas e Tubulões
O SISEs disponibiliza os seguintes tipos de estacas:
i. Escavada: Pequeno diâmetro, grande diâmetro e com lama bentonítica;
ii. Pré-moldada: Cravada ou prensada;
iii. Franki: Fuste apiloada ou fuste vibrado;
iv. Outras: Strauss, Hélice Contínua, Raiz, Metálica, Injetada sob alta pressão ou Não-Padrão.
As estacas podem ser verticais ou inclinadas, onde os blocos de capeamento podem ser definidos de dois tipos: flexíveis ou rígidos. Para o primeiro tipo, sua geometria é retangular, podendo conter até 12 estacas. Para o bloco rígido, suageometria pode ser triangular, retangular, pentagonal ou hexagonal, veja Fig. 4.
Para o elemento de tubulão, sua geometria é de fuste e de base circular, estando associado apenas um pilar para cada tubulão.
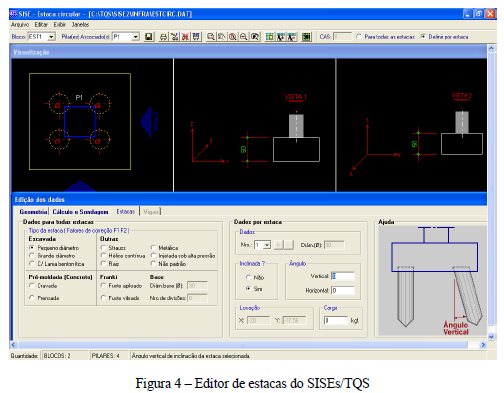
3.2 Detalhamento dos Perfis de Sondagens
O cálculo dos fatores de influência do solo no SISEs/TQS é baseado na intercorrelação dos dados advindos dos perfis de sondagens editados pelo usuário, com os modelos de cálculo desenvolvidos pelo SISEs/TQS.
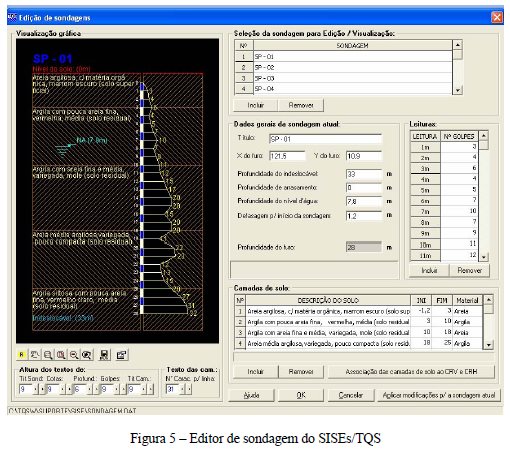
Os perfis de sondagens são introduzidos em um editor de fácil entrada e de visualização imediata. Assim, adiciona-se um perfil, suas coordenadas na obra, cota do nível de água, cota do indeslocável (caso seja atingida na sondagem), os valores de resistência à penetração (SPT), a classificação das camadas, etc., conforme Fig. 5.
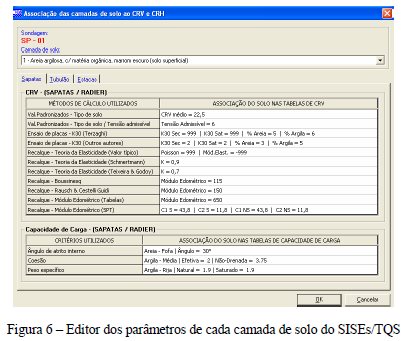
Para cada camada de um perfil de sondagem, o sistema exige a associação deste com um certo valor de tabela ou a um certo modelo a ser usado para cálculo dos seus coeficientes de influência do solo desta camada de metro em metro. Esta escolha também depende do tipo de elemento de fundação, ver Fig. 6.
Em função da grande variabilidade de dados de sondagens obtidos numa mesma obra, o que é característico na área de fundações, o SISEs/TQS disponibiliza cinco opções para que o usuário associe, conforme seu critério de projeto, as diversas sondagens existentes, podendo escolher, para cada tipo de elemento de fundação, uma das seguintes opções:
• Média ponderada entre as duas sondagens mais próximas;
• Média ponderada entre todas as sondagens;
• Média aritmética entre todas as sondagens;
• Sondagem mais próxima;
• Sondagem específica, conforme seleção do usuário.
Deste modo, o sistema monta os valores de influência do solo de cada ponto da fundação em função do critério de ponderação adotado pelo usuário para cada sondagem.
3.3 Modelos matemáticos para representar o solo: Histórico Geral
Existem diversos procedimentos empregados para a simulação do solo. Entretanto, quatro métodos são os que mais se destacam na literatura sobre o assunto, sendo os seguintes: a) Analítico; b) Camada Finita; c) Discreto Contínuo, MEF ou MEC; d) Mola Equivalente ou Modelo de Winkler.
Os modelos a) e b) são pouco utilizados de modo geral, pois são de aplicações restritas com relação à limitação de tipo de geometria, carregamento ou material. Mas para consulta sobre estes métodos, pode-se citar as seguintes referências: Burmister (1945), Poulos (1967), Chan et al. (1974), Davies & Banerjee (1978), Gibson (1967, 1974) para o caso a); e Booker et al. (1989), Lee & Small (1991), Southcott & Small (1996) e Ta & Small (1998), para o caso. b.
Os dois últimos casos, c) e d), representam os procedimentos mais empregados para a simulação do solo. O caso c) utiliza os potentes métodos numéricos, mais precisamente o emprego do método de elementos finitos (MEF) e o de elementos de contorno (MEC).
O MEF é a mais versátil e poderosa ferramenta usada em problemas de análise estrutural.
No entanto, para o caso de ser aplicado na análise de domínio infinito (solos), é uma ferramenta difícil na preparação dos dados, onerosa para o seu armazenamento e resolução do sistema final, além de exigir certos cuidados para a imposição de restrições de deslocamentos para a simulação de domínios infinitos, uma vez que a sua formulação clássica é baseada na imposição de condições de contornos. Para o caso 3D, isto se torna ainda mais contundente, uma vez que é necessário usar centenas ou milhares de elementos finitos do tipo sólido.
Assim, poucos pesquisadores têm empregado o MEF na análise de maciços, citando-se os trabalhos de Ottaviani (1975) e Chow & Teh (1991).
O MEC é uma ferramenta adequada para a análise do solo, devido às suas características peculiares: i) funções ponderadoras que já contemplam as condições de contorno atendidas a grandes distâncias; e ii) exige que a região em contato com o solo seja discretizada. Na análise de sapatas sobre o solo 3D é necessário apenas a representação do solo com a malha 2D desta fundação, ao passo que o MEF exige uma discretização tridimensional do problema.
A solução de Mindlin (1936) é o principal ponto de partida para a construção das funções ponderadoras a serem empregadas pelo método. Entretanto, ela é apenas válida para um meio homogêneo e semi-infinito, o que também restringe a aplicação em propósitos genéricos, uma vez que o solo é intrinsecamente não-homogêneo e com a possibilidade da camada indeslocável ser prescrita em projeto. Neste caso, é comum usar um expediente não correto sob o ponto de vista do formalismo matemático, mas que não afeta muito as respostas finais, que é o modelo simplificado e prático de Steinbrenner (Poulos, 1967). Este expediente emprega a solução de Mindlin, calculando os deslocamentos de um determinado ponto e subtraindo-se este do deslocamento surgido na cota indeslocável: ( ρxSteinbrenner=ρx Mindlin-ρhMindlin) onde ρx é o deslocamento na cota x e ρh é o deslocamento na cota do plano indeslocável.
Este modelo simplificado também leva em conta a não-homogeneidade do maciço. Citam-se nesta linha de aplicação os trabalhos de Almeida & Paiva (2004), Antunes & Iwamoto (2000), Holanda Jr. (1998) e Maier & Novati (1987).
Para o caso d), o meio contínuo é substituído por um sistema de molas equivalente e discreto, também conhecido como modelo de Winkler. A maior vantagem na aplicação deste modelo é sua simplicidade e relativa facilidade para implementação computacional. Este argumento se consolida ainda mais quando se integra ao solo os elementos de fundação e de edifício baseado no MEF. Uma vez que as características de esparsidade e simetria da matriz de rigidez final não se perdem, fato bastante relevante em termos de menor armazenamento e velocidade de cálculo na resolução do sistema linear para problemas de médio e grande porte processados em microcomputadores, principalmente para o caso de se considerar efeitos não lineares, expediente considerado no sistema TQS.
A maior desvantagem deste método é com respeito à escolha dos módulos de reação da mola para representar o maciço. Esses parâmetros deveriam ser calculados experimentalmente para cada perfil do solo, mas, na prática, é comum empregá-los em outros perfis com características diferentes, o que pode levar as soluções incertas e imprecisas. Nessa linha, desenvolvem-se os trabalhos de Mylonakis & Gazetas (1998), Lee (1993), Randolph & Wroth (1979) e Cheung & Zienkiewicz (1965).
3.4. Representação do solo adotado pelo SISEs/TQS
O SISEs/TQS foi desenvolvido a partir do modelo de Winkler. Tal escolha foi tomada em função da obrigatoriedade de se ter um sistema solo/estrutura com propósitos genéricos no tocante a análise e projetos estruturais, procurando aproveitar o sistema CAD/TQS já consolidado, como os sistemas de lançamentos e cálculo de elementos finitos, da montagem e resolução do sistema linear e não-linear. Uma vez que tais mudanças implicariam na criação de modelos mecânicos e numéricos novos que deveriam ser testados exaustivamente e - mesmo assim - teriam um período de maturação no meio técnico. Além disso, quaisquer outra escolha implicaria numa grande quantidade de dados para armazenamento e processamento, somados aos já existentes no complexo modelo de edifício do CAD/TQS, quer seja usando o MEF 3D, quer seja usando o MEC 3D.
Assim, para considerar a influência do solo junto à fundação, partiu-se da hipótese de Winkler, que estabelece que as tensões aplicadas no solo sejam proporcionais, em uma relação escalar ao recalque mobilizado; não havendo influência entre o ponto de aplicação desta tensão com sua vizinhança.
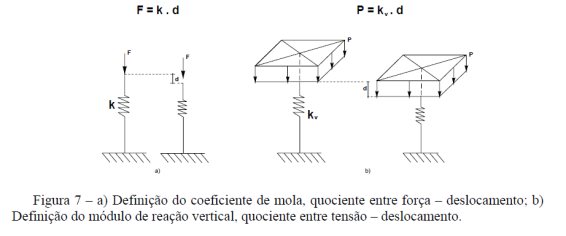
Ou seja, estabelece uma relação pontual entre fundação-solo, mediante a definição de uma constante de mola que representará a rigidez do maciço. Para isto, é necessário definir o valor de Kv e Kh e o qual é denominado de módulo de reação vertical e horizontal. Este é um valor escalar que representa o coeficiente de rigidez que o solo possui para resistir ao deslocamento mobilizado por uma tensão imposta. Ele é análogo ao coeficiente de mola, mas não relacionado a uma força, mas sim a uma tensão (força por área). Veja exemplo esquemático na Fig. 7 para melhor entendimento.
Neste sentido, a TQS Informática Ltda procurou na literatura e nos centros de pesquisas do Brasil diversas metodologias usuais que empregam este modelo de molas. Para o caso das fundações diretas, dividiu-se em três diferentes categorias de cálculo destes coeficientes: 1) Valores padronizados; 2) Ensaio de Placa; e 3) Recalque vertical estimado.
A seguir, é definido e apresentado cada uma dessas categorias, bem como as referências dos métodos que foram implementados no SISEs/TQS. Convêm destacar que todas as expressões, tabelas e gráficos relativos a todos os métodos listados em seguida já estão inseridos no SISEs/TQS, bastando ao usuário selecionar suas opções. Além disso, sãopossíveis que sejam inseridos outros valores nas tabelas conforme critério de cada projetista.
3.4.1. Valores Padronizados (VP)
Vários pesquisadores apresentam tabelas e ábacos que relacionam o módulo de reação com o tipo de solo. Estes valores foram obtidos em ensaios in situ em regiões e condições específicas, conforme podem ser averiguados nas referências bibliográficas indicadas. Assim, os seus valores podem não ser representativos em certas condições, devendo ficar a critério do profissional o seu uso. Foram considerados três métodos nesta categoria, os quais são:
• Tipo de Solo: Moraes (1981);
• SPT – Tensão Admissível: Morrison (1993);
• Tipo de Solo - Tensão Admissível: Cintra et al. (2003), Morrison (1993).
3.4.2. Ensaio de Placa (EP)
São chamados também de métodos racionais, onde os parâmetros de deformabilidade são obtidos in situ ou em laboratórios mediante o ensaio de provas de carga em placas. Os ensaios mais conhecidos são os apresentados nas tabelas de:
• Terzaghi: Velloso & Lopes (1996), Terzaghi (1955);
• Outros autores: ACI (1988), Calavera (2000), Bowles (1997).
3.4.3. Recalque Vertical Estimado (RE)
De acordo com a definição de módulo de reação vertical, que pode ser escrito como:
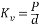 (1)
(1)
onde P e d representam a tensão atuante e o deslocamento mobilizado na fundação, conforme esquematizado na Fig. 7b.
É possível estimar o coeficiente vertical (kv) a partir do cálculo do recalque da fundação sobre o maciço mobilizado por uma tensão unitária. Os métodos desenvolvidos nesta categoria foram:
• Teoria da Elasticidade/ Valor Típico: Teixeira & Godoy (1996), Poulos & Davis (1974);
• Teoria da Elasticidade / Schmertmann: Cintra et al. (2003), Schmertmann (1978);
• Teoria da Elasticidade / Teixeira & Godoy: Trofimenkof (1974);
• Schultze & Sherif: Moura (1995), Schultze & Sherif (1973);
• Parry: Moura (1995), Parry (1971), Parry (1978);
• Boussinesq: Moraes (1981), Poulos & Davis (1974);
• Rausch & Cestelli Guidi: Moraes (1981);
• Módulo Edométrico – Tabelas: Boussinesq (1885), Holl (1940), Poulos & Davis (1974);
• Módulo Edométrico – SPT: Schultze & Menzenbach (1961).
4. EXEMPLOS NUMÉRICOS
Apresenta-se a seguir dois exemplos onde foram comparadas as respostas obtidas pelo SISEs/TQS com os verificados na literatura. O primeiro é um exemplo clássico apresentado na literatura internacional e o segundo teve o intuito de verificar a influência nos recalques na presença de duas sapatas, confrontado as respostas com um modelo numérico de referência.
4.1. Sapata sobre uma base não-deformável
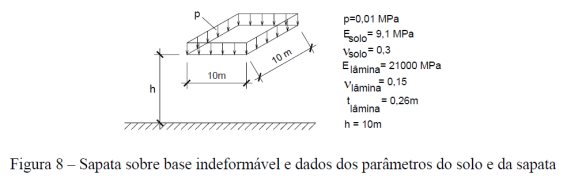
Este exemplo avalia uma sapata isolada apoiada sobre um meio homogêneo com a base indeformável a uma distância de 10 m. A geometria e as propriedades relevantes para sua simulação são apresentadas na Fig. 8.
Considerou-se o SISEs/TQS com apenas um pilar ligado a fundação, desconsiderando o peso próprio e forças concentradas no pilar. Foi ajustado um valor de peso próprio para a sapata (1,92 tf/m3) de modo a resultar em um carregamento idêntico ao indicado na literatura.
A discretização adotada no SISEs/TQS está esquematizada na Fig. 10.
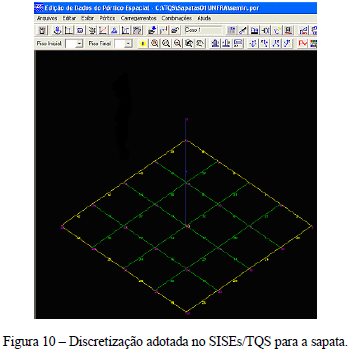
Apresentam-se para o SISEs/TQS as respostas para o método baseado na Teoria da Elasticidade (TE), que utiliza as relações de Poulos & Davis (1974) junto com o procedimento de Steinbrenner para representar a base indeformável. Neste caso, é necessário alimentar no SISEs/TQS o módulo de deformabilidade e o coeficiente de Poisson do solo. Assim, no editor de sondagem, admitiu-se um perfil de solo com uma camada única de areia com SPT constante para simular meio homogêneo e a cota do indeslocável. Para o método denominado TE/Típico usa-se os valores sugeridos por Teixeira & Godoy (1996) para estes dois parâmetros elásticos. Para o método TE/Schmertmann o módulo de elasticidade, proposto por Schmertmann (1978), é dado pela seguinte relação válida para fundações diretas:
E = 3⋅ K ⋅ SPT (2)
onde K depende do tipo de solo, e são indicados valores típicos por Teixeira (1993).
Para o método chamado de TE/ Teixeira & Godoy , o módulo de deformabilidade é dado por Teixeira & Godoy (1996), onde se estabelece a seguinte relação para fundações diretas:
E =α ⋅ K ⋅ SPT (3)
onde α é um coeficiente que correlaciona a resistência de ponta (qc) com o SPT, onde seus valores para a areia e argila foram propostos por Trofimenkov (1974).
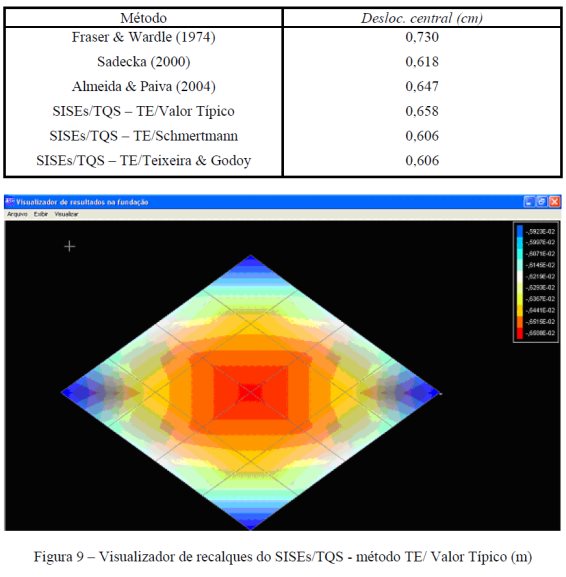
A Tabela 1 apresenta as respostas obtidas por diversas metodologias e pelo SISEs/TQS, verificando-se que os valores estão bem próximos entre si, apenas havendo uma maior distorção com relação ao trabalho de Fraser & Wardle (1974), que modelam o espaço sem infinito usando a técnica dos elementos de superfície, onde a matriz final de influência é obtida usando-se as técnicas de transformações de integral. Sadecka (2000) avalia os deslocamentos ao longo da profundidade do meio através de funções pesos não lineares, e admite-se a influência da lâmina (placa) apoiada na superfície do solo usando o MEF.
Almeida & Paiva (2004) utilizam o MEC para simular o solo e o MEF para representar a sapata, sendo o sistema final muito oneroso do ponto de vista de tempo de resposta e de armazenamento das matrizes de influência do solo e da fundação.
Tabela 1. Deslocamentos verticais para o centro da sapata:
4.2. Efeito de Influência entre 2 Sapatas
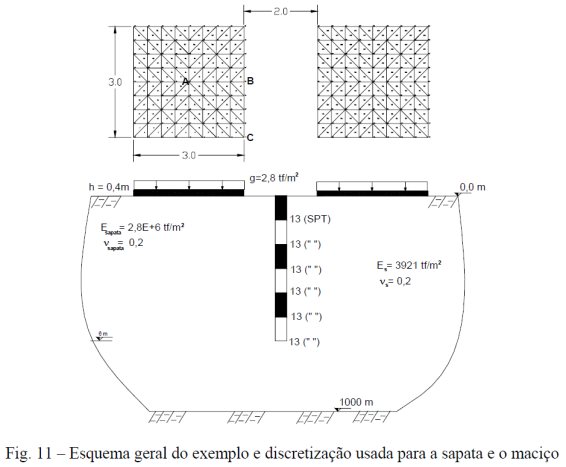
Este exemplo compara a influência que duas sapatas vizinhas têm sobre os valores de recalques. Pois o método de cálculo do SISEs/TQS é o de mola de Winkler, que – como principal deficiência - não leva em conta a presença num certo ponto dos efeitos de forças aplicados em outros pontos vizinhos nos coeficientes do solo. Assim, a Fig. 11 apresenta o exemplo, indicando os valores empregados, e a discretização usada para simulá-lo pelo MEF.
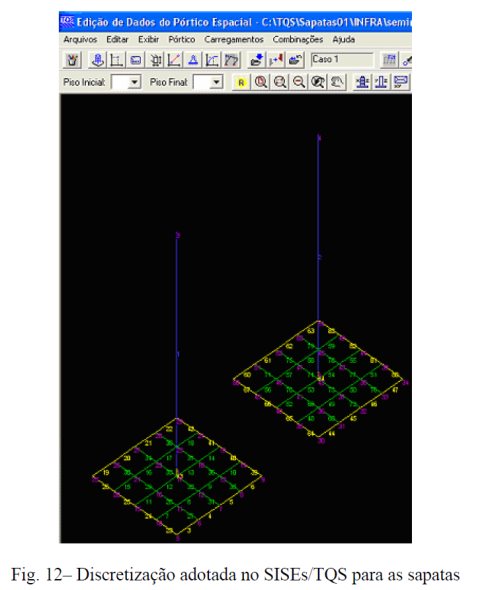
Aplicou-se um peso próprio sobre os elementos de fundação de valor = 3,5 tf/m3 de modo que a resultante em cada sapata fosse de 25,2 tf. Isto dividido pela área da sapata (9m2) resulta em 2,8 tf/m2, conforme valor de projeto, Fig. 11. A discretização adotada para as sapatas pelo SISEs/TQS está indicada na Fig. 12. Considerou-se no editor de sondagens do SISEs/TQS um SPT constante com a profundidade para indicar um meio homogêneo, com valor igual ao indicado na Fig. 11, onde a cota do indeslocável foi estabelecida e uma distância de 1000 m para representar o meio semi-infinito. Comparou-se este exemplo com a formulação desenvolvida em Almeida & Paiva (2004)
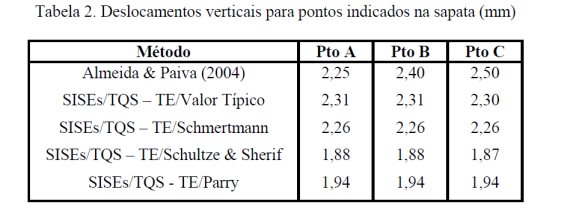
Na Tabela 2, os modelos do SISEs/TQS - TE/Valor Típico e SISEs/TQS – TE/Schmertmann são os mesmos apresentados no exemplo anterior. O modelo de SISEs/TQS – TE/Schultze & Sherif, detalhado em Moura (1995), é baseado na estimativa de recalques em solos arenosos, onde se estabelece uma expressão que leva em conta a geometria da sapata, sua profundidade no maciço, a tensão aplicada, um SPT médio obtido dentro do bulbo de pressões e a relação entre a cota de assentamento e a cota do indeslocável. O modelo de SISEs/TQS - TE/Parry, Moura (1995), apresenta uma expressão paracálculo do recalque em que computa o valor médio do SPT, a geometria e a cota de assentamento da fundação, a espessura da camada compressível e a posição do lençol freático.
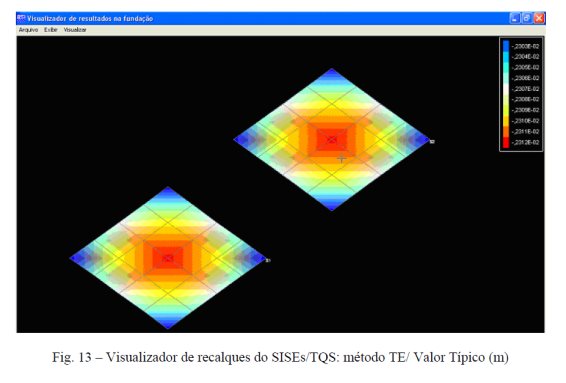
A Tabela 2 e a Fig. 13 indicam as respostas obtidas, demonstrando boa concordância entre os diversos métodos. A diferença percentual obtida, para o caso do centro e vértice da sapata entre o método contínuo e o SISEs/TQS – TE/Schmertmann é de -0,4% e 9,6%, respectivamente, o que, em termos de projeto, são pequenos. É válido destacar que as respostas obtidas pelo SISEs/TQS obtêm valores mais próximos tanto para o centro como para o vértice da sapata. Entretanto, este valor médio do SISEs/TQS está dentre os extremos do modelo contínuo. Além disso, a influência das duas sapatas nas respostas não indicaram uma diferença discrepante entre as duas diferentes metodologias de cálculo, validando o procedimento de cálculo do SISEs/TQS.
Em Almeida & Paiva (2004), os pontos B e C, em função da influência das duas sapatas, possuem recalques mais acentuados, o que está de acordo com o esperado. No SISEs/TQS, os pontos A, B e C possuem os mesmos valores de recalques para os modelos empregados. Isto porque os fatores de influência obtidos no SISEs são iguais para todos os pontos da fundação, exceto nos nós de extremo onde se é considerado uma área de influência que é a metade do valor da área dos nós fora do contorno. Soma-se também que o modelo presente não leva em conta a influência da vizinhança no computo da influência do solo.
5. CONCLUSÕES
O artigo teve o intuito de apresentar um novo ferramental para a aplicação em projetos e em pesquisas no campo da análise de problemas de interação solo-estrutura. Conforme demonstrado no artigo, existem diversas metodologias queavaliam o problema. Entretanto, estes procedimentos apresentam restrições quanto a sua aplicabilidade em propósitosgenéricos na análise de edifícios.
O desenvolvimento do SISEs/TQS tem dois pontos principais como premissa: primeiro em apresentar um modelo numérico que seja capaz de reproduzir de maneira satisfatória o comportamento mecânico do conjunto solo-estrutura. Eo segundo, em disponibilizar um sistema cuja editoração, geração de malha e análise, sejam fáceis, tudo isto sem perder sua característica principal que é a possibilidade de modelagem de edifícios reais, incluindo efeito de segunda ordem, lajes via elementos finitos, elementos de fundações mistos, etc.
Para o primeiro caso, avaliaram-se dois exemplos para fundações rasas, os quais foram comparados com valores apresentados na literatura internacional sobre o assunto, onde as respostas obtidas no SISEs/TQS demonstraram boa concordância com outras formulações, como as advindas de métodos semi-analíticos ou dos métodos numéricos, por exemplo, o método de elementos de contorno.
A segunda premissa também foi atingida, pois a TQS informática Ltda possui uma vasta experiência no desenvolvimento de sistemas computacionais na parte gráfica e sistemas de interface com o usuário. Acrescenta-se também que o sistema CAD/TQS possui uma grande aceitação e confiança por parte dos projetistas e por pesquisadores em diversos centrosacadêmicos do Brasil, como ferramental de análise de edifícios em concreto armado.
Por fim, o artigo é o primeiro a ser apresentado com referência ao desenvolvimento do SISEs - Sistema de Interação Solo Estrutura. Pretende-se, em outras publicações, apresentar de maneira mais específica as diversas possibilidades deaplicações do sistema, como por exemplo a análise de um edifício real considerando o efeito de segunda ordem, a interação entre elementos mistos de fundação (estacas com sapatas), a influência da laje maciça, o efeito de vento, etc, todas estas possibilidades disponíveis no SISEs/TQS.
REFERÊNCIAS
ACI, 336.2 R, 1988. Suggested design procedures for combined footing and mats. American Concret Institute.
Almeida, V.S., Paiva, J.B., 2004. A mixed BEM-FEM formulation for layered soilsuperstructure interaction. Engineering analysis with boundary elements. v. 28, p. 1111- 1121.
Antunes, H.M.C.C., Iwamoto, R. K., 2000. Comparação entre resultados observados in situ e modelos numéricos para a interação solo-estrutura. In: Simpósio de Interação Estrutura- Solo em Edifícios. Programas de Pós-Graduação em Geotecnia e Engenharia de Estruturas da USP/SC.
Associação Brasileira de Normas Técnicas, 1996. NBR 6122: Projeto e execução de fundações.
Associação Brasileira de Normas Técnicas, 2000. NBR 6118: Projeto e Execução de Obras de concreto armado.
Booker, J.R., Carter, J.P. & Small, J.C. , 1989. Some recent applications of numerical methods to geotechnical analysis.Computers & Structures, v. 31, n.1, p. 81-92.
Boussinesq, J., 1885. Application des potentiels à l’étude de l’équilibre et du mouvements des solides élastiques. Gauthier-Villard, Paris.
Bowles, J., 1997. Foundation Analisis and Design. Mc Graw-Hill.
Burmister, D.M., 1945. The general theory of stresses and displacements in layered systems I. Journal of Applied Physics, v.16, p.89-96.
Calavera, J., 2000. Cálculo de estructuras de cimentación, 4 Ed. Intemac.
Chan, C.M., Micleborough, N.C. & Ning, F., 2000. Analysis of cracking effects on tall
reinforced concrete building. Journal os Structural Eng. vol. 126, n. 9, p. 995–1003.
Chan, K.S., Karasudhi, P. & Lee, S.L., 1974. Force at a point in the interior of a layered elastic half-space. Int. J. Solids Structs., v. 10, p. 1179- 1199.
Cheung, Y.K., Zienkiewicz, O.C., 1965. Plates And Tanks On Elastic Foundations – An Application Of Finite Element Method.Int. J. Solids Struct., V. 1, P. 451-461.
Chow, Y.K., Teh, C.I., 1991. Pile-cap-pile-group interaction in nonhomogeneous soil. Journal of Geotechnical Engineering , v. 117,n. 11, p. 1655-1668.
Cintra, J.C.A., Aoki, N. & Albiero, J.H., 2003. Tensão admissível em fundações diretas. Ed. Rima.
Davies, T.G., Banerjee, P.K., 1978. The displacement field due to a point load at the interface of a two layer elastic half-space. Géotechnique, v. 28, n.1, p. 43-56.
Franco, M., 1995. Global and local instability of concret tall buildings. In: SIMPOSIUM ON SPACE STRUCTURES, Milan, May. Procedings.
Franco, M., Vasconcelos, A.C., 1991. Practical assessment of second order effects in tall buildings. In.: COLLOQUIUM ON THE CEB-FIP MC90, Rio de Janeiro. Procedings.p. 307-324.
Fraser, R.A., Wardle, L.J., 1974. Numerical analysis of rectangular rafts on layered foundations. Géotechnique, v. 26, p. 613-630.
Gibson, R.E., 1967. Some results concerning displacements and stresses in a nonhomogeneous elastic half-space.Géotechnique, v. 17, p. 587-567.
Gibson, R.E., 1974. The analytical method in soil mechanics. Géotechnique, v. 24, p. 115- 140.
Gusmão, A. D., 1990. Estudo da Interação Solo-estrutura e sua influência em recalques de edificações. 165p. Tese (Doutorado) – Universidade Federal do Rio de Janeiro, COPPE.
Holanda Jr., O. G., 1998. Interação solo-estrutura para edifícios de concreto armado sobre fundações diretas. São Carlos. 191p. Dissertação (Mestrado) – Escola de Engenharia de São Carlos, Universidade de São Paulo.
Holanda Jr., O. G., 2002. Influência de recalques em edifícios de alvenaria estrutural. São Carlos. 224 p. Tese (Doutorado) – Escola de Engenharia de São Carlos, Universidade de São Paulo.
Holl, D.L., 1940. Stress transmission in earth. Proc. High. Res. Board, vol. 20, pp. 709-721.
Kim, J.K., Lee, T.G., 1993. Failure behaviour of reinforced concrete frames by the combined layered and nonlayered method. Computers & Structures, v. 48, n.5, p. 819-825.
Lee, C.Y., 1993. Pile Group Settlement Analysis By Hybrid Layer Approach. Journal Of Geotechnical Engineering, V.119, N.6, P. 984-997.
Lee, C.Y., Small, J.C., 1991. Finite Layer Analysis of Laterally Loaded Piles in Cross- Anisotropic Soils. International Journal for Numerical Methods in Geomechanics, v. 15, p.785-808.
Lopes, F. R., Gusmão, A.D., 1991. On the influence of soil-structure interaction in the distribution of foundation loads and settlements. In. EUROPEAN CONFERENCE ON SOIL MECHANICS AND FOUNDATION ENGINEERING,10., Firenze.Proceedings. Rotterdam, A.A Balkema, v.2,p. 505-509.
Maier, G., Novati, G., 1987. Boundary element elastic analysis by a sucessive stiffness method. Int. J. for Numerical and Anal. Methods in Geomechanics, v.11, p. 435-447.
Mamaghani, I.H.P., Aydan, O. & Kajikawa, Y., 1999. Analysis of masonry structures understatic and dynamic loading by discrete finite element method. Journal of Structural Mechanics and Earthquake Engineering, v. 16, n.2, p. 75-86.
Martins, C. H., 2001. Análise não-linear de estruturas tridimensionais de edifícios de andares múltiplos com núcleos resistentes, considerando a rigidez trasnversal à flexão das lajes, 252p. Tese (Doutorado) – Escola de Engenharia de São Carlos, USP.
Mindlin, R.D., 1936. Force at a point in the interior of a semi-infinite solid. J. Physics, v.7, p. 195-202.
Moraes, M. C., 1981. Estruturas de Fundações. Mc Graw - Hill do Brasil, 3a.ed.
Morrison, N., 1993. Interacción suelo-estructuras: semi-espaço de Winkler. Universidad Politécnica de Cataluna, Barcelona-Espanha.
Moura, A.R.L.U. de, 1995. Interação Solo-Estrutura em edifícios. Recife. 135p. Dissertação (Mestrado) – Universidade Federal de Pernambuco. CT Engenharia Civil.
Mylonakis, G., Gazetas, G., 1998. Settlement And Additional Internal Forces Of Grouped Piles In Layered Soil.Géotechnique, V. 48,N.1, P. 55-72.
Noorzaei, J., Godbole, P. N. & Viladkar, M. N., 1993. Non-linear soil-structure interaction of plane frames: a parametric study. Computers & Structures, v. 49, n.3, p. 561-566.
Oliveira, R. S., 2001. Análise de pavimentos de edifícios de concreto armado com a consideração da não-linearidade física – modelagem e metodologia de aplicação a projetos, 197p. Tese (Doutorado) – Escola de Engenharia de São Carlos, USP.
Ottaviani, M., 1975. Three-dimensional finite element analysis of vertically loaded pile groups. Géotechnique, v. 25, n.2, p. 159-174.
Parry, R.H.G., 1971. A direct method of estimating settlements in sand from SPT values. Proccedings Simp. on the interaction of structures and foundation, Birmingham, p. 29-32.
Parry, R.H.G., 1978. Estimating foundation settlements in sand from plate bearing tests. Géotechnique, London, 28 (1): 107-118.
Pimenta, P.M., Yojo, T., 1992. Análise geometricamente exata de pórticos através do método dos elementos finitos. In: XIII CILAMCE, v.1, Anais, p. 191-199.
Pinto, R. S., 2002. Análise não-linear das estruturas de contraventamento de edifícios em concreto armado, 189p. Tese (Doutorado) – Escola de Engenharia de São Carlos, Universidade de São Paulo.
Poulos, H.G., 1967. Stresses and displacements in an elastic layer underlain by rough rigid base. Géotechnique, v.17, p. 378-410.
Poulos, H.G., Davis, E.H., 1974. Elastic solutions for soil and rock mass. New York, John Wiley & Sons 535p.
Ramalho, M. A., Correa, M. R. S., 1991. Interação solo-estrutura para edifícios sobre fundação direta. In. JORNADAS SUL-AMERICANAS DE ENGENHARIA ESTRUTURAL, 25., Porto Alegre. Anais. Porto Alegre, UFGRS, v.2, p.433 -444.
Randolph, M. F., Wroth, C. P., 1979. An Analysis Of The Vertical Deformation Of Pile Groups. Géotechnique, V. 29, P. 423-439.
Reis, J.H.C., 2000. Interação solo-estrutura de grupos de edifícios com fundações superficiais em argila mole. São Carlos. 148p. Dissertação (Mestrado) – Escola de Engenharia de São Carlos, Universidade de São Paulo.
Romanel, C., Kundu, T., 1990. Soil-structure interaction in a layered medium. Int. J. Engng. Sci., v.28, p. 191-213.
Romanel, C., Veiga, J., Roehl, D., 2000. Aplicação da transformada de Fourier na análise de problemas solo-estrutura tridimensionais. In: XXI CILAMCE- CONGRESSO IBERO LATINO DE MÉTODOS COMPUTACIONAIS EM ENGENHARIA. Rio de Janeiro.
Sadecka, L., 2000. A finite/infinite element analysis of thick plate on a layered foundation. Computers & Structures, v. 76, p. 603-610.
Schmertmann, J.H., 1978. Estimating settlements. Guidelines for cone penetration test – performance and design, Federal Highway Adm., FHWA-TS-78-208, Jul, Cap. 6, p. 49-56.
Schultze, E., Menzenbach, E., 1961. Standard Penetration Test and compressibility of soils. Paris, França, vol.1.
Schultze, E., Sherif, G., 1973. Prediction of settlements from evaluated settlement observations for sand. Proc. 8th International Conference on soil mechanics and foundation
Engineering, Moscow, vol.1.3, pg. 225 – 230. Smith, B. S., Coull, A., 1991. Tall Building Structures. Analysis and Design. Wiley Interscience Publication.
Soriano, H.L., 2003. Método de Elementos Finitos em Análise de Estruturas. São Paulo: Editora da Universidade de São Paulo.
Southcott, P.H., Small, J.C., 1996. Finite layer analysis of vertically loaded piles and pile groups. Computer andGeotechnics, v. 18, n.1, p. 47-63.
Ta, L.D., Small, J.C., 1998. Analysis and performance of piled raft foundations on layered soils-case studies. Soil and Foundations, v.38, n.4, p. 145-150.
Taranath, B.S., 1988. Structural analysis and design of tall building. McGraw Hill.
Teixeira, A.H., 1993. Um aperfeiçoamento das sondagens de simples reconhecimento à percussão. Anais da mesa redonda Solos do interior de São Paulo, p. 75-93.
Teixeira, A.H., Godoy, N.S., 1996. Análise, projeto e execução de fundações rasas. Fundações: teoria e prática, Hachich et al. (editores), Ed. Pini, SP, Cap. 7, p. 227-264.
Terzaghi, K., 1955. Evaluation of coefficient of subgrade reaction. Géotechnique, vol. 5, no. 4, pp. 297-326.
Trofimenkof, J.G., 1974. Penetration testing in eastern Europe. Proc. European Symposium on Penetration Resistance,Stockolm, vol. 2.1, p. 24-28.
Vecchio, F.J., Emara, M.B., 1992. Shear deformations in reinforced concrete frames. ACI Structural Journal, v. 89, n.1.
Velloso, D. A., Lopes, F.R., 1996. Fundações: Critérios de Projeto, Investigação do Subsolo, Fundações Superficiais. COPPE, UFRJ, pg.169.
