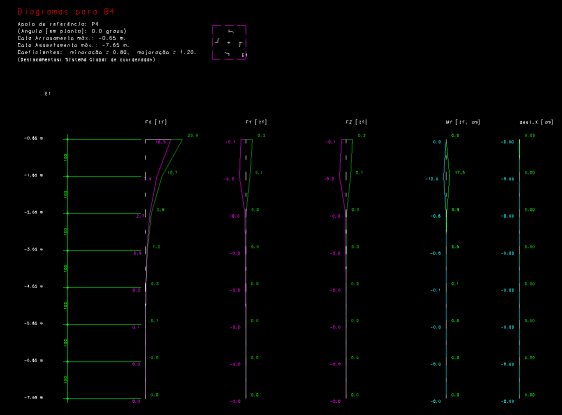
SISEs – Parte 10 – Fundações em bloco sobre 3 estacas sem baldrame e sobre 1 estaca com baldrame
Seguindo o assunto da Interação entre estrutura, fundação e solo, vamos apresentar agora outras duas possíveis soluções, tendo sempre como meta a estabilidade da estrutura, a adequação e uma melhor correspondência entre o modelo analisado e a estrutura real.
Solução 2:
Para esta condição também, os momentos fletores, oriundos da superestrutura (de acordo com as ações consideradas no projeto), precisam ser absorvidos pela fundação – as estacas. Porém, neste caso específico, os efeitos das flexões podem ser “transformados” em binários (forças de reação, nas estacas, que se contrapõem a cada esforço de flexão, transmitido ao bloco de fundação), em ambas as direções.
Verificou-se a dimensão mínima destas estacas Ø = 30 cm, de forma a atender as exigências de cargas e tensões admissíveis. O espaçamento entre as estacas é de 90 cm, para anular possíveis esforços resultantes de tração, em qualquer estaca.
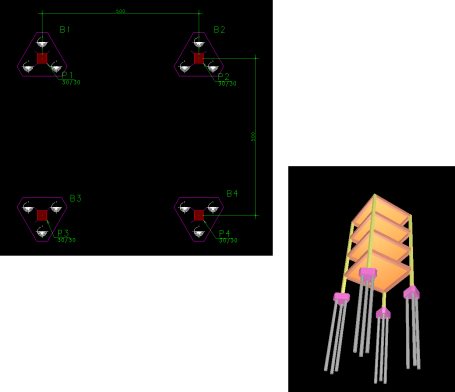
1 – Coeficientes de mola sem majoração
Como descrito anteriormente, para que o modelo considerasse que os esforços de flexão fossem, a priori, “convertidos” apenas em binários nas estacas, definimos neste modelo articulações no topo (interface entre a estaca e o bloco de fundação) de cada estaca.
Observe, porém que, de acordo com os diagramas a seguir, ainda apareceram momentos fletores nos pontos intermediários das estacas discretizadas, decorrentes da aplicação da força horizontal do pórtico na base do pilar e da ação/reação entre as estacas e o solo.
De acordo com critérios pré-definidos, pelo sistema SISEs, as verificações de capacidade de carga, tensões admissíveis e ocorrência de tração, por estaca, são automaticamente efetuadas pelo sistema e incluídas nas mensagens de avisos e erros.
O diagrama de momentos fletores para toda a estrutura (super e infra) é apresentado abaixo. Unidades: tf*m.
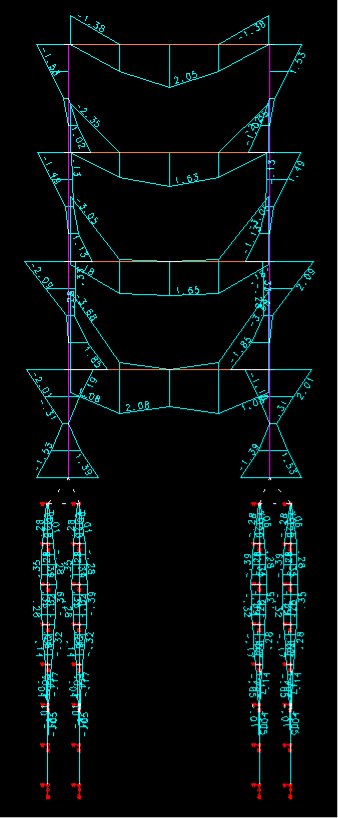
Algumas verificações simples sobre a estabilidade do modelo integrado (com a interação Solo-Estrutura):
- Coeficientes Gama Z (γz): 1.051
- Deslocamentos Horizontais: 0.38 cm (H/2828), entre pavimentos: 0.12 cm (Hi/2337.)
O comportamento da estrutura melhorou significativamente com o “engastamento” na base dos pilares se comparado com a solução anterior de uma estaca por pilar.
Como se pode notar pelo diagrama acima, as estacas ainda estão submetidas a esforços de flexão. O valor máximo do momento fletor foi de 39.2 tf*cm a 2 m de profundidade. Na seção transversal da estaca a esta profundidade, temos ainda tensões de tração na borda da estaca. A estaca também necessita ser armada até uma determinada profundidade.
2 – Coeficientes de mola majorado em 10x
O diagrama de momentos fletores para toda a estrutura (super e infra) é apresentado abaixo. Unidades: tf*m.
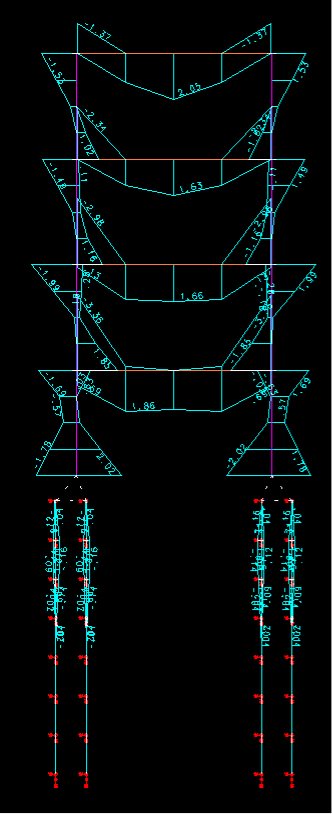
Como se pode notar pelo diagrama acima, as estacas ainda estão submetidas a esforços de flexão. O valor máximo do momento fletor foi de 15.9 tf*cm a 1 m de profundidade. Na seção transversal da estaca a esta profundidade, temos ainda tensões de tração na borda da estaca.
3 – Coeficientes de mola infinito
Para simular o que é feito na prática de projeto neste caso e poder comparar com os resultados obtidos no sistema, vamos aumentar os vínculos elásticos / coeficientes de mola para um valor muito alto (infinito).
O diagrama de momentos fletores que obtivemos é o abaixo.
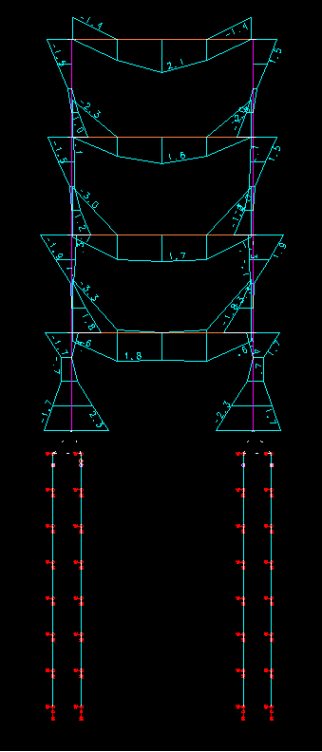
Podemos observar que os momentos fletores nas estacas desapareceram. A força horizontal que aparece na base do pilar da estrutura é absorvida no topo da estaca na sua totalidade. A estaca agora não necessita mais de armação pois ela não apresenta nenhum ponto de tração ao longo da sua extensão.
Detalhe de desenho, gerado pelo SISEs, com os resultados (esforços e deslocamentos) principais em uma estaca:
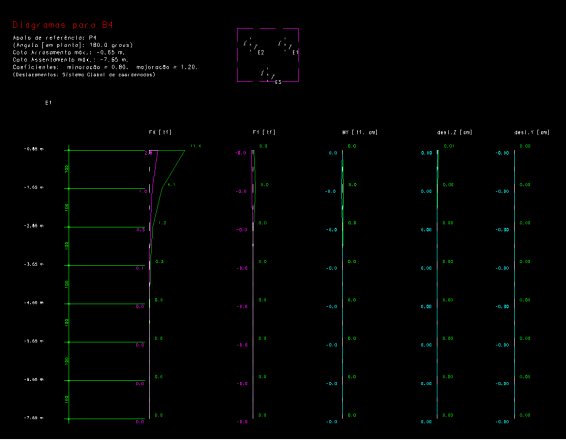
Este é o procedimento adotado por muitos engenheiros quando a força horizontal no pé do pilar é desprezada.
Solução 3:
Para esta solução, como se pode observar na planta a seguir, foram definidas vigas, interligando cada bloco de fundação, para que haja um travamento, em cada uma das direções principais, de cada bloco.
Definimos as dimensões para estas vigas como sendo de 20 x 40 cm.
Verificou-se a dimensão mínima para estas estacas, com diâmetro Ø = 40 cm.
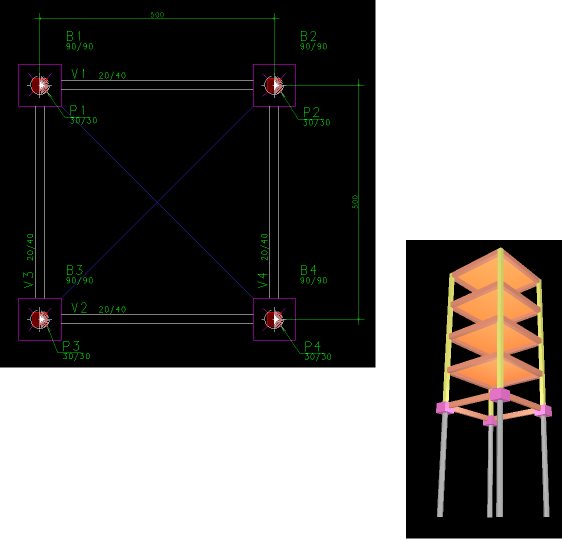
A ideia deste modelo é de que as vigas-baldrame equilibrem as flexões, atuantes nos pilares, em todas as solicitações determinadas para a estrutura, em ambas as direções. E que, também, “absorvam” parte dos esforços horizontais no carregamento de cargas verticais.
Com a condição de que as vigas baldrame “absorvam” os momentos fletores nas bases dos pilares, as estacas então ficam encarregadas apenas de absorverem os esforços verticais e parte dos horizontais.
Veja a ilustração a seguir, com o esquema sugerido para a vinculação real do apoio nos elementos da estrutura, vinculação correspondendo a uma articulação para não transmissão de momentos à fundação (as estacas irão substituir estes apoios e, portanto, receber as forças verticais e horizontais da estrutura).
Ilustração em corte (sem escala) do esquema proposto de vinculações:
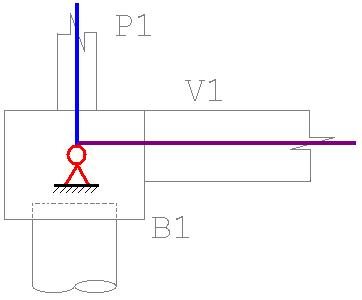
Para implementar estas características no modelo, a partir do Modelador estrutural, basta alterar, para ambas as direções, as restrições de apoio dos elementos de fundação, na própria planta da fundação, para cada elemento:
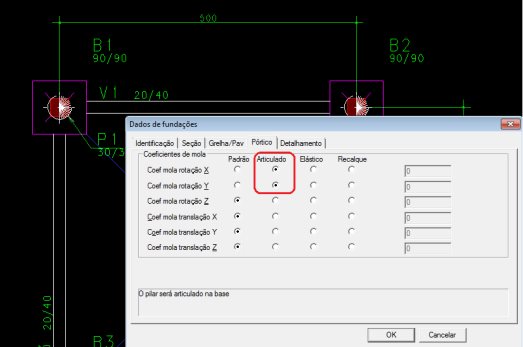
Com o modelo definido, vamos então ao estudo dos casos.
1 – Coeficientes de mola sem majoração
Para nos certificarmos da entrada correta destas vinculações, basta observar os diagramas resultantes, em cada direção. O diagrama abaixo representa uma envoltória para todos os carregamentos gerados de cargas verticais e horizontais.
O diagrama de momentos fletores para toda a estrutura (super e infra) é apresentado abaixo. Unidades: tf*m.
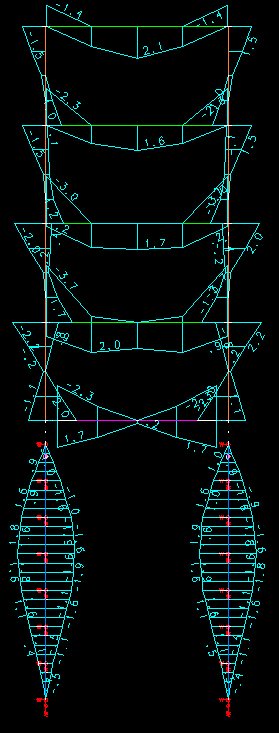
Algumas verificações simples sobre a estabilidade do modelo integrado (com a interação Solo- Estrutura):
Coeficientes Gama Z (γz): 1.045
Deslocamentos Horizontais: 0.32 cm (H/3386), entre pavimentos: 0.08 cm (Hi/.)
O comportamento da estrutura melhorou significativamente também, com a implementação das vigas-baldrame entre os blocos de fundação, se comparado com a primeira solução proposta, de uma estaca por pilar, SEM as vigas.
Observe porém que, de acordo com o diagrama anterior, os momentos fletores nos pontos intermediários das estacas discretizadas, decorrentes da aplicação da força horizontal do pórtico na base do pilar e da ação/reação entre as estacas e o solo, obrigam também o dimensionamento e detalhamento de armaduras, nas estacas. Estes diagramas surgiram devido à ação da carga horizontal de vento. Numa direção, o total de carga horizontal devido ao vento chegou a 1.85 tf. Note que não existe outra possibilidade de transmissão desta carga horizontal para o solo a não ser através do fuste das estacas (não temos estacas inclinadas). Apenas para a carga vertical, como a estrutura é simétrica, as cargas horizontais na base do pilar não são transmitidas a fundação e provocam tração nas vigas-baldrame.
O valor máximo do momento fletor foi de 188 tf*cm a 3 m de profundidade.
2 – Coeficientes de mola majorados em 100x
O diagrama de momentos fletores para toda a estrutura (super e infra) é apresentado abaixo. Unidades: tf*m. O diagrama abaixo (My) representa uma envoltória para todos os carregamentos gerados de cargas verticais e horizontais.,
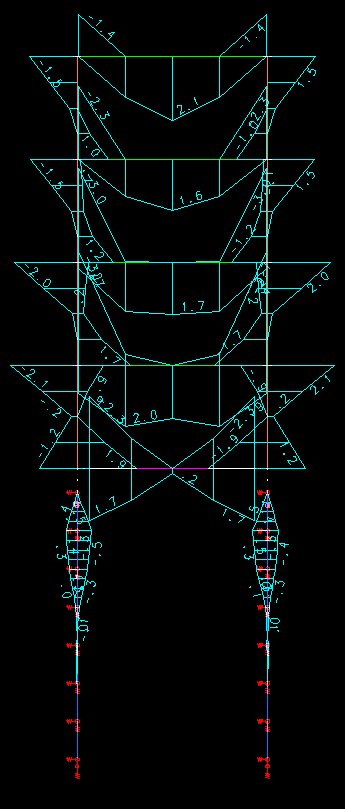
Como se pode notar pelo diagrama acima, mesmo com esta grande majoração da resistência do solo, as estacas ainda acusam esforços de flexão. O valor máximo do momento fletor foi de 47.4 tf*cm a 1 m de profundidade. A estaca também necessitaria ser armada até uma determinada profundidade. A força horizontal devido ao vento é transmitida ao solo através da flexão nas estacas. O coeficiente de mola maior adotado neste caso provoca a absorção destas forças em regiões superiores da estaca reduzindo os valores da flexão.
3 – Coeficientes de mola infinito
Simulando novamente o que é, às vezes, feito na prática de projeto, aumentamos os vínculos elásticos / coeficientes de mola para um valor muito alto.
O diagrama de momentos fletores nesta condição fica praticamente igual ao anterior (na parte da superestrutura), alterando-se significativamente apenas os esforços nas estacas. Ali é que se observa que as flexões simplesmente “desapareceram”, junto, inclusive, com as forças horizontais. Neste caso a força horizontal foi absorvida integralmente no primeiro vínculo elástico no topo da estaca. Observe o detalhe, pelo desenho gerado pelo SISEs: