SISEs – Parte 9 – Fundações em bloco sobre uma estaca sem baldrame

Neste texto será falado um pouco da interação entre pilares, vigas e lajes de uma edificação usual com os elementos estruturais de estabilidade e o solo.

Neste caso vamos abordar a questão da fundação em estacas, especificamente uma estaca sob pilar. Este é um caso interessante, pois o solo deve ser, obrigatoriamente, considerado para dar condições de estabilidade a estrutura.

Este tipo de estrutura é, aparentemente, simples. Entretanto, cuidados especiais devem ser tomados, pois a análise conjunta entre a estrutura, estaca e presença do solo leva a considerações não muito intuitivas.

A análise feita está mais preocupada com os esforços solicitantes em todo o conjunto estrutura + estaca. Com a obtenção de solicitações satisfatórias, o dimensionamento e o detalhamento estrutural se tornam possíveis. É evidente que também que foi feita as verificações estruturais necessárias para a estrutura e a estaca (estabilidade, capacidade admissível da estaca, seção transversal adequada, etc.).

O modelo será teórico, cujo principal objetivo é de apresentar e raciocinar sobre este comportamento conjunto entre estrutura/fundações e solo. Além da estrutura de concreto armado em si, estamos também alimentando a sondagem do solo, características geométricas da estaca e critérios de projeto para determinação das vinculações elásticas (molas) na estaca representando o solo (teoria de Winkler).

Portanto, todas as variáveis acima são bem conhecidas do engenheiro estrutural com exceção dos critérios para determinação das molas. Para as molas verticais adotamos o cálculo da capacidade de carga da estaca através do processo Aoki-Lopes, processo bem conhecido de todos. O método Aoki-Lopes também considera e calcula recalque da estaca para um determinado carregamento considerando o efeito das demais estacas (grupo). Com o recalque e a carga ao longo da estaca, basta dividir uma grandeza pela outra que obtemos as molas verticais distribuídas.

Para as molas horizontais a situação é mais indefinida. Temos dois processos básicos, um deles depende da característica do material e o outro depende dos valores obtidos pelo SPT do terreno. Neste exemplo será adotado o método que detende do SPT, pois ele vai refletir melhor as variações das camadas do solo e medidas nas sondagens. Cabe aqui lembrar que, devido a imprecisão na obtenção destes valores, a representação do solo deve ser feita sempre com valores máximos e mínimos das grandezas e, posteriormente, adota-se uma envoltória final para detalhamento.

Descrição do projeto

O projeto terá 4 pavimentos na superestrutura, com 4 pilares quadrados (30x30 cm), lajes de altura de 10cm, 4 vigas de 30x40cm, em cada pavimento (com exceção da fundação) e vãos de 5m:

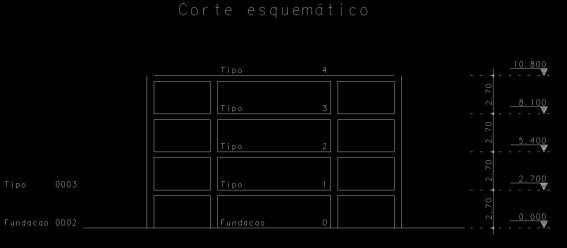
Dimensões do pavimento Tipo:

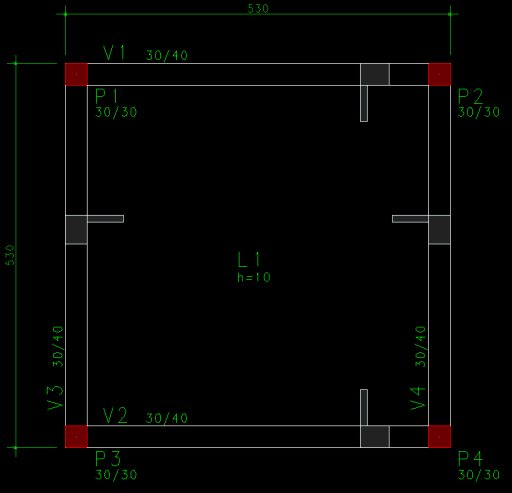
Cargas consideradas na laje: 0,1tf/m2 de carga permanente e 0,15tf/m2 de carga acidental.

Foram também considerados 4 casos de vento:

 Sondagem:

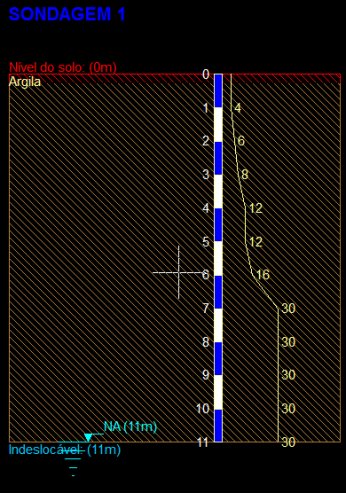
Estaca: tipo hélice contínua, tensão admissível de 40kgf/cm2 ,fator de segurança 2 e comprimento da estaca de 7m.

Modelos estudados

• Solução 1: Blocos sobre 1 estaca, SEM vigas baldrames entre os blocos
• Solução 2: Blocos sobre 4 estacas, SEM vigas baldrames entre os blocos
• Solução 3: Blocos sobre 1 estaca, COM vigas baldrames entre os blocos

Neste e-mail, iremos tratar apenas da Solução 1, devido a extensão do assunto.

Solução 1:

1 – Coeficiente de mola sem majoração

Para esta condição, os momentos fletores, oriundos da superestrutura, precisam ser absorvidos pela fundação (estacas), visto que cada pilar está ligado diretamente com o seu devido elemento de fundação. Nestes termos, verificou-se a dimensão mínima destas estacas: ∅=60cm, para eliminar os avisos de capacidade de carga, tensões excedidas, deslocamentos limites, instabilidades da estrutura, etc.

Com isso, surge a necessidade das estacas serem armadas, para combate aos esforços devido às flexões , transmitidos às estacas através dos blocos de fundação, cujas armaduras também devem ser dimensionadas e detalhadas.

Modelo da fundação em planta:

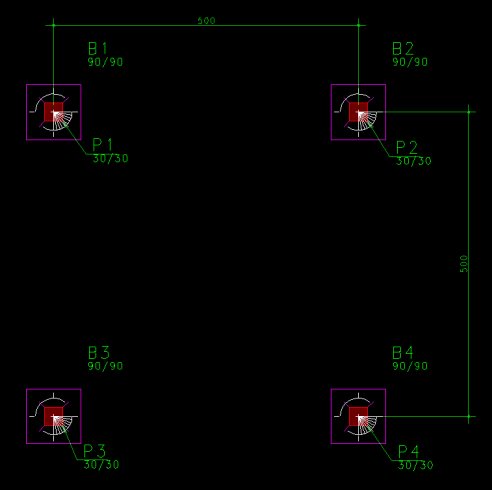
Modelo 3D de toda estrutura + estacas:

O pórtico espacial resultante, para este caso, será como o que segue abaixo, onde se observa a infra-estrutura discretizadae agregada à superestrutura (através de novos nós e vínculos elásticos), formando-se então um novo pórtico espacial – um modelo integrado e único – com a presença do efeito do solo:

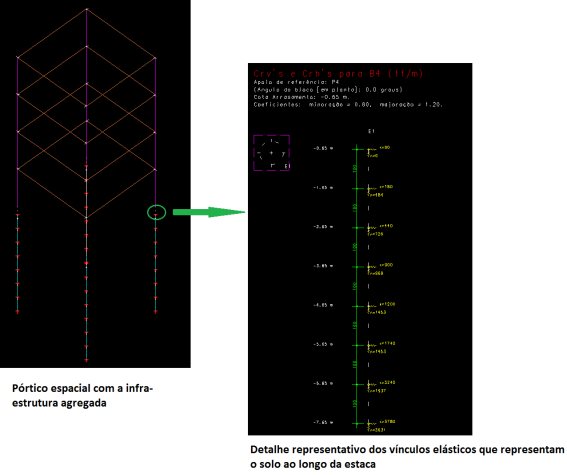
Os principais resultados obtidos podem ser verificados graficamente, tanto na visualização do Pórtico Espacial (esforços e deslocamentos), quanto nos desenhos que o SISEs nos fornece, de forma concisa. 

Detalhe de visualização de diagramas, pelo pórtico espacial, específico para o esforço (My) e carregamento acima (envoltória):

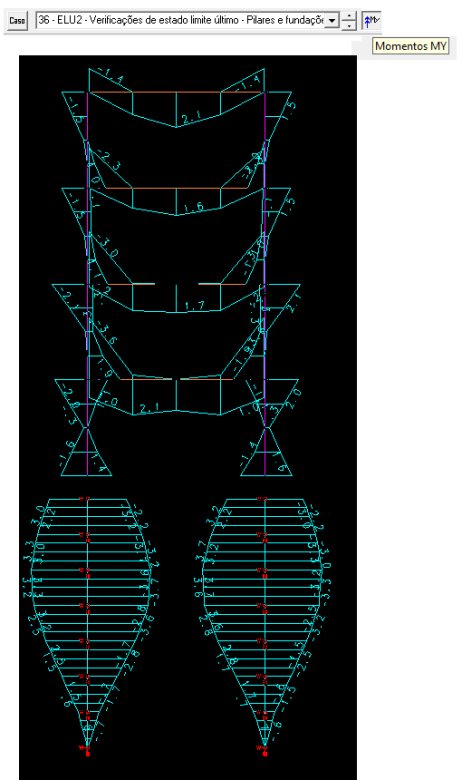
Deve-se notar que o momento fletor na estaca foi maior do que no pilar. Sem a colaboração da estaca a flexão, a estrutura não fica estável. As armaduras dos pilares devem ter emendas com as armaduras das estacas. Não estamos estudando ainda os efeitos de segunda ordem do conjunto pilar + única estaca.

Desenho gerado pelo SISE, com os resultados (esforços e deslocamentos, selecionáveis pelo usuário) para o Bloco B4.

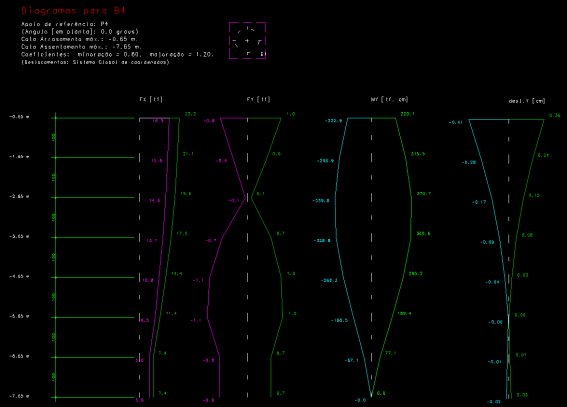
Observe pelo diagrama acima que o momento fletor máximo na estaca não está no topo e sim num ponto intermediário, igual a 370.7 tf*cm. Sob o ponto de vista do concreto, a estaca passou, armada. Com esta magnitude de momentos fletora estaca tem regiões de tração. Sob o ponto de vista do solo, a capacidade de carga da estaca atendeu plenamente.

Algumas verificações simples sobre a estabilidade do modelo integrado (com a interação Solo- Estrutura):

Coeficientes Gama Z (γz ): 1.050

Deslocamentos Horizontais: 0.39 cm (H/2768), entre pavimentos: 0.11 cm (Hi/2410).

Para estacas com diâmetros inferiores a Ø = 60 cm, não se consegue, através deste modelo, obterse como resultado uma estrutura estável. O sistema acusa coeficientes de Gama Z (γz) elevados, deslocamentos horizontais globais e entre pavimentos excessivos, etc. Portanto, sem elementos de travamento na fundação, necessita-se de estacas de diâmetro Ø = 60 cm, armaduras nas estacas e o comprimento destas armaduras em quase toda a estaca. Não estamos estudando aqui com profundidade os métodos construtivos para a execução desta armadura.

2 – Coeficientes de mola majorados em 10x

Vamos apresentar abaixo os diagramas de momentos fletores no conjunto estrutura/fundação com os coeficientes de mola nas estacas multiplicados por 10 vezes:

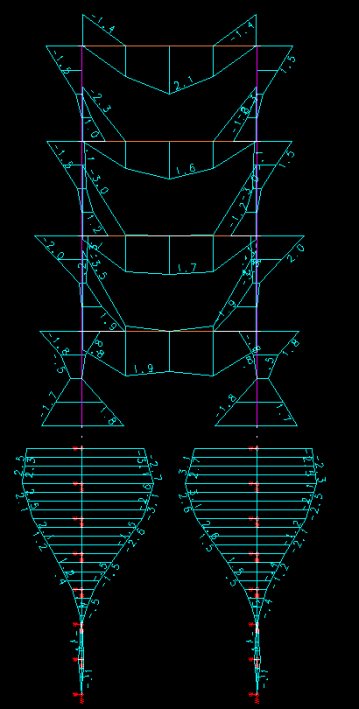
A primeira observação a ser feita é que o aumento do vínculo elástico horizontal em 10 vezes não alterou significativamente os resultados de momentos fletores. Com o maior engastamento da estaca no solo, os momentosfletores na estaca se reduziram. Mesmo assim é necessária a armação nas estacas. Os momentos fletores na base do pilar aumentaram.

3 - Pilar Articulado e Coeficientes de Mola Normais

Muitos colegas acham que simplesmente articular a base do pilar resolve o problema dos momentos fletores na estaca. Vamos apresentar abaixo o mesmo diagrama de momentos fletores para este caso.

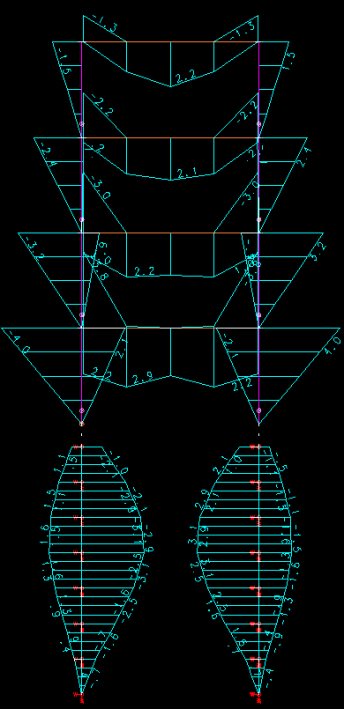
No diagrama acima dá para notar que os momentos fletores positivos no pilares e na viga do primeiro pavimento do pórtico aumentaram e o que é o principal: os momentos fletores na estaca não foram eliminados. Devido a componente horizontal da força na base do pilar, os momentos fletores aparecem ao longo do fuste do pilar. Apenas no topo da estaca o momento fletor é nulo. O edifício também sofreu deslocamentos horizontais maiores e o Gama Z aumentou (1.075). Esta solução também não é uma boa solução. A estaca também necessita ser armada.

Aproveitando a oportunidade, vale aqui lembrar também de outra observação interessante que, infelizmente, não é tão rara quanto se pensa: a passagem dos valores de cargas da estrutura para a fundação considerando apenas a carga vertical. Se a estrutura é engastada a rotação e a translação horizontal, a presença de momentos fletores e forças horizontais são fundamentais para o seu equilíbrio. Se a fundação não for projetada para tais solicitações, todo o conceito de projeto está deficiente com consequências imprevisíveis.

4 - Estrutura Engastada ( sem fundação projetada)

Observe os diagramas a seguir para este mesmo projeto, considerando as bases dos pilares com “engaste perfeito”:

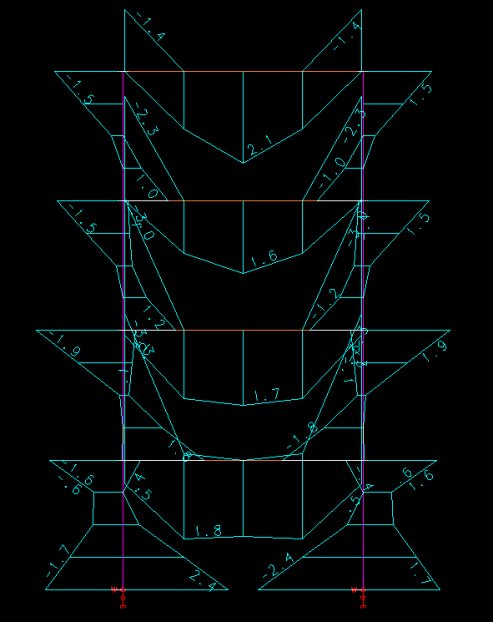
Detalhe da envoltória dos momentos My (base dos pilares e 1º. lance), considerando o pórtico da estrutura com “engastamentos perfeitos”.