Dados Modais Simplificados

Dados Modais Simplificados

A análise modal efetuada pelo TQS considera que, de modo geral, todos os nós da estrutura possuem algum valor de massa. Esta massa é calculada em função dos carregamentos atuantes nas barras que chegam nestes nós e diretamente nos nós.

Assim, após a análise estrutural e modal, o número de nós e graus de liberdades existentes é grande e pode levar a uma pós-análise demorada ou mesmo impossível.

No caso de túneis de vento, é comum que estes trabalhem com modelos simplificados para a análise dos modos de vibração de edifícios altos para facilitar as análises e entendimento global dos efeitos atuantes na estrutura. Apesar de simplificado, este modelo é totalmente adequado para as análises.

O modelo simplificado utilizado é tal que, para cada pavimento, toda a massa do pavimento é concentrada em apenas um nó e existem apenas 3 graus de liberdades: translação em X, translação em Y e rotação em torno de Z. De modo visual, teríamos o seguinte:

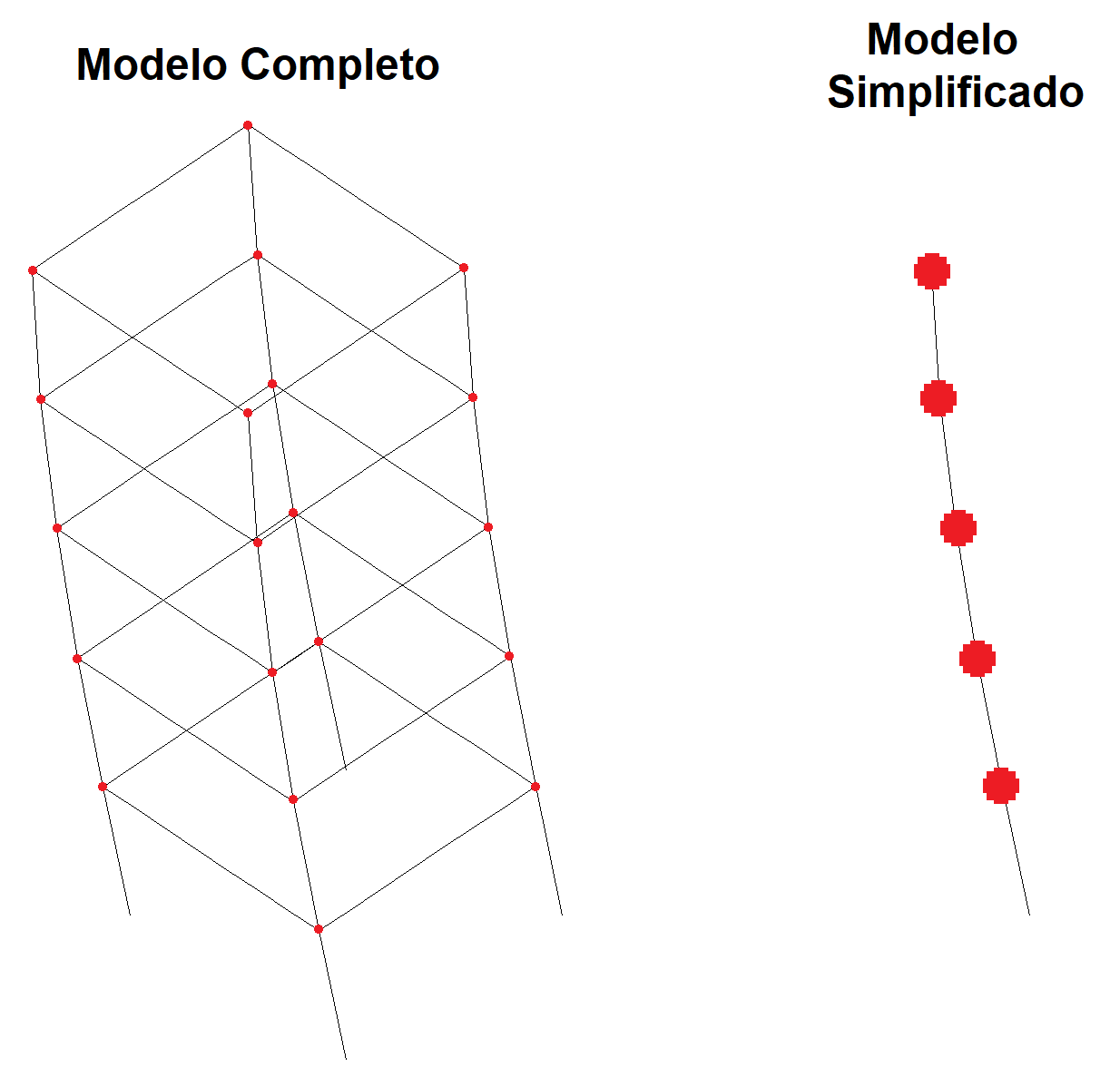
d9c5bc855863d3ddbac8beef65d8237d.png

Definição das massas e centro de massa (CM)

Para cada pavimento, a massa utilizada para os graus de liberdade associados as translações são obtidas diretamente da somatória das massas associadas a cada um dos nós:

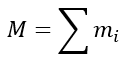
cb4adfca896c4282bdee37d3cdad9dc9.png

O centro de massas (CM), onde haverá o único nó do pavimento, é obtido como a média ponderada das coordenadas dos nós e da massa de cada nó:

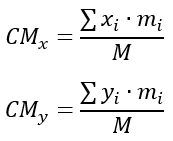
f28e437cb884b14ec81621a970b11b09.png

Por fim, o momento de inércia de massa em relação ao eixo Z (I) é obtido por:

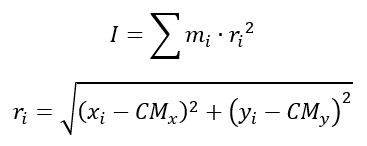
f93c2d1a0395319397e9fb57ee755dbe.png

Definição das formas modais

A conversão das formas modais do modelo completo para o modelo do pavimento é feita, primeiramente, isolando os nós de cada pavimento.

Posteriormente, considerando que o pavimento é um diafragma rígido, e se desloca, no plano do próprio pavimento, como um corpo rígido, temos o seguinte:

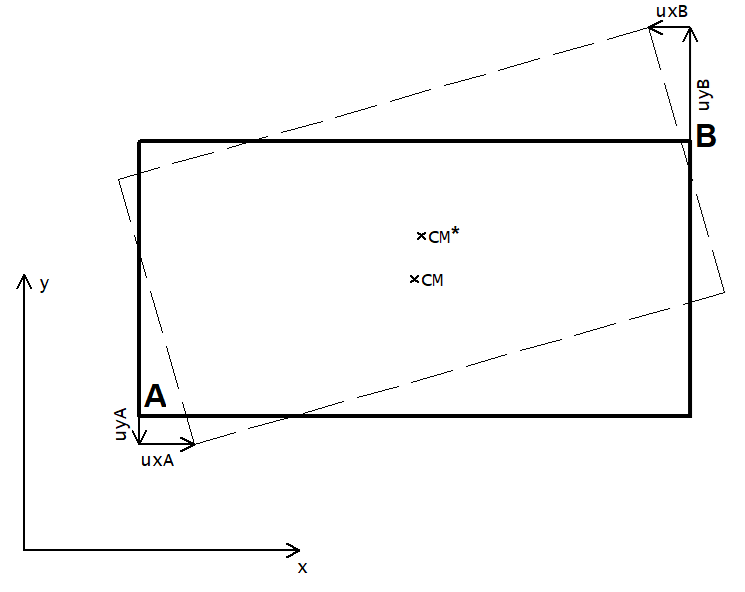
aad47cd08cf6e4f47a8a807a3969fcac.png


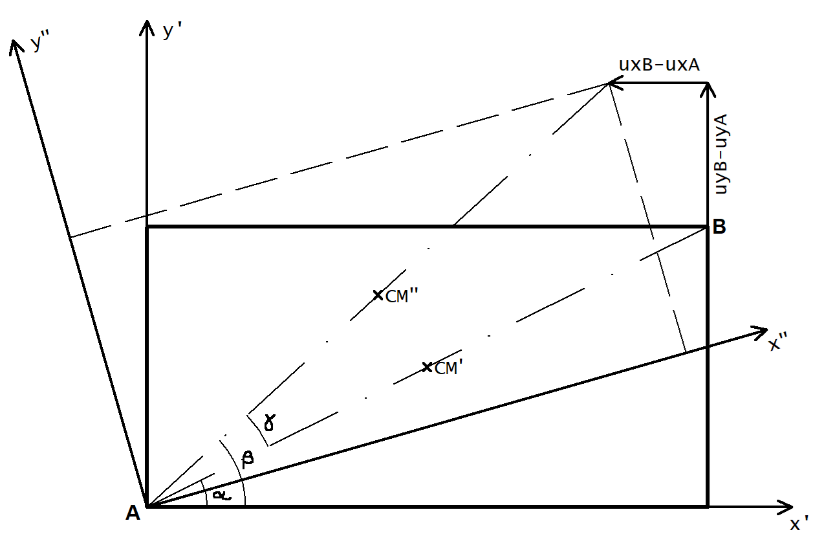
137b0ca385e1f6f06a71598ebc9dc0b1.png


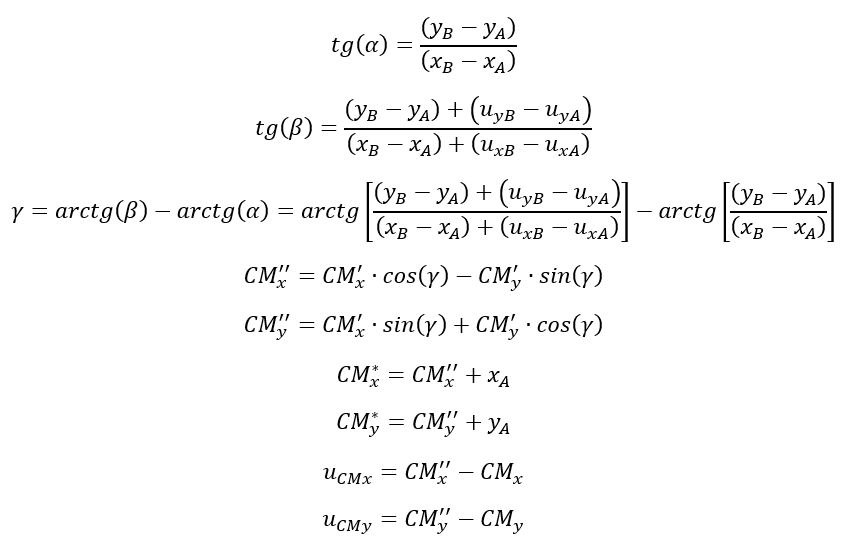
6e693cbe0c5e0f76a9555d0624719fa2.png

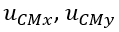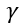Os valores ded1c5d29d0ba95d1ff3aa233ee30edf.pnge 99916275e4655fa204503e9daf10cdc3.png representam os “deslocamentos” e rotação do centro de massa da forma modal. A definição destes valores é feita para cada uma das formas modais calculadas do modelo estrutural.

A seleção dos pontos A e B é feita para cada pavimento de modo que o ponto A represente o nó do modelo estrutural mais à esquerda/abaixo (quadrante 3) e o ponto B represente o nó do modelo estrutural mais à direita/acima (quadrante 1).

Verificação de ortogonalidade

Após a obtenção das formas modais e massas do modelo simplificado, é feita a verificação de ortogonalidade destes dados.

A priori, os modos de vibração do modelo completo são ortogonais, de modo que:

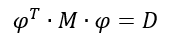
b55cb8ac0dc03de666018825269c2f8d.png

Onde:

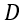a57c8d333662b984bce42b258e43eab1.png : é uma matriz ortogonal;

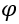5716070811e0b9d91bf672cc91ca064b.png : é a matriz com modos de vibração originais;

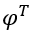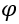69833968a1557abe6d15f412ff60ccd7.png : é a transposta de 5716070811e0b9d91bf672cc91ca064b.png;

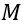0a320cc5a8bc60d88f1ad100c0925c9f.png : é a matriz de massa que pode é aproximada por uma matriz diagonal onde cada elemento 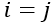2e8ae734868654afb9d1947c9fcc3742.png corresponde à massa de cada grau de liberdade.

Tomando apenas um modo de vibração teríamos:

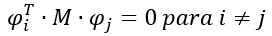
123f2a6d0a853f507782261c348f91f7.png

Como cada modo de vibração é um autovetor, podemos afirmar que: se 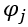4394244aa4f8d89180cb71831964460f.png é um modo de vibração, 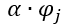6976e83cd7fcea6ffa38ad528adf9482.png também é um modo de vibração ( é um número qualquer). Ou seja, podemos multiplicar 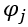4394244aa4f8d89180cb71831964460f.png por um número qualquer tal que:

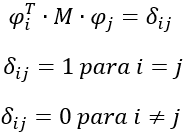
5b4cd5902306d1c2f87fc07d2bc53a0e.png

Neste caso, diz-se que os modos estão normalizados.

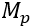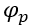Quando a redução do modelo completo para o modelo simplificado (sub-índice p) é feita, estamos buscando um conjunto ecd88a34040a1faf03d01eea3f3c5eeb.png e 92f5af6198b9d47441da0730e7dec419.png que seja representativo.

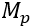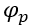Se os modos de vibração originais estavam normalizados, e o conjunto ecd88a34040a1faf03d01eea3f3c5eeb.png e 92f5af6198b9d47441da0730e7dec419.png é realmente representativo, então temos:

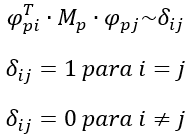
02ea7790126529275c89dab8587657e7.png

Esta aproximação costuma ser adequada para a maioria dos casos, tendo alguma falha em estruturas onde algum dos modos de vibração não está diretamente ligado a torre “como um todo”.

No caso de um dos modos de vibração da estrutura simplificada não ser ortogonal, o arquivo de saída indicará isso.

Geração dos arquivos

A geração dos arquivos com os dados modais simplificados é feita através do Visualizador de Análise Dinâmica, existente dentro do sistema Pórtico-TQS. Dentro do Visualizador de Análise Dinâmica, execute: "Vento" - "Exportar" - "Modelo Simplificado".

Após o processamento serão gerados 4 arquivos dentro da pasta "Espacial" do edifício. São eles:

  • Modal_General_Data.LST
  • Dados gerais do edifício e nível dos pavimentos;
  • Modal_Mass_Distribution.LST
  • Massa, centro de massa, momento de inércia da massa para cada pavimento;
  • Modal_Mode_Shapes.LST
  • Período, frequência e forma modal de cada modo de vibração;
  • Modal_Orthogonality.LST
  • Relatório de verificação de ortogonalidade

Como a maioria dos túneis de vento se encontra fora do Brasil, estes relatórios foram desenvolvidos na língua inglesa, de modo a ter melhor entendimento pela equipe do túnel.

Verificação mínima

O engenheiro estrutural responsável pelo projeto deve fazer a verificação da ortogonalidade dos modos simplificados, para ter certeza que o conjunto simplificado é representativo do conjunto original.

Para isso, é necessário acessar o relatório "Modal_Orthogonality.LST". Neste relatório é apresentada uma matriz. Todos os elementos da diagonal desta matriz devem ser próximos do valor 1.00. Todos os demais valores devem ser próximos do valor 0.00.




Análise Modal - Modelo VI
Aceleração pela NBR 6123

Consulte também